Problema Tairos – OJI 2019, Clasa a 11-a

• Dificultate:
• Autor: Radu Muntean
• Online: InfoArena, PbInfo

Rezumat

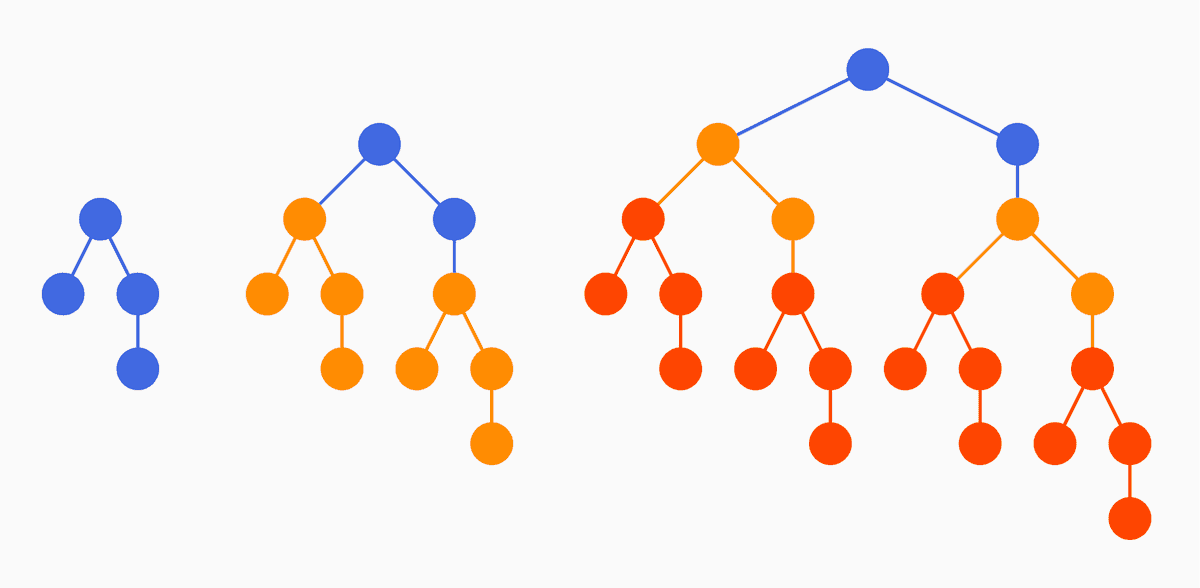
Se dă un arbore cu $n$ noduri și cu rădăcina în nodul $1$ Acesta va fi modificat în mai multe etape. În fiecare etapă, se ia fiecare frunză din arborele curent și se înlocuiește cu o copie a arborelui inițial. Procedeul se repetă la infinit. Să se determine câte noduri din arborele infinit se află la distanța $d$ de rădăcină. Rezultatul va fi calculat modulo $10^9 + 7$

Soluție

Dacă numerotăm nivelurile arborelui infinit de la $0$ atunci trebuie să determinăm numărul de noduri de pe nivelul $d$ În primul rând, sper să nu vă sperie faptul că arborele este infinit. Îl putem considera doar suficient de mare încât să nu mai putem crea noduri pe nivelul $d$

Orice nod de pe nivelul $d$ trebuie să fie un nod non-frunză de pe nivelul $x$ al unei copii a arborelui inițial care a înlocuit la un moment dat o frunză de pe nivelul $d - x$ Recitiți cu mare atenție această propoziție, pentru că aici stă cheia problemei. Să dau și un exemplu totuși:

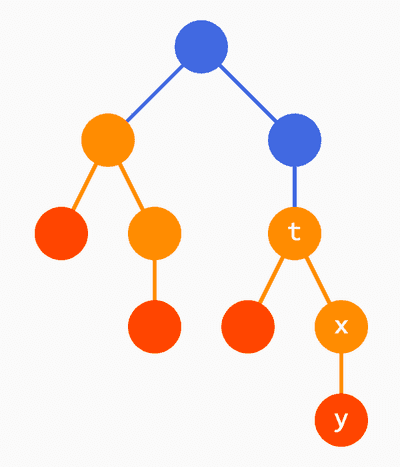
Aici nodul $x$ se află pe nivelul $3$ din arborele infinit, și totodată pe nivelul $1$ din arborele portocaliu cu rădăcina în $t$ aflat pe nivelul $3 - 1 = 2$ Cât despre nodul $y$ putem fi tentați să afirmăm că se află pe nivelul $2$ al arborelui cu rădăcina în $t$ dar de fapt se află pe nivelul $0$ al arborelui roșu cu rădăcina în $y$ De asta mai sus am folosit termenul non-frunză. Când un nod pare a fi frunză într-un subarbore identic cu cel original, el este de fapt rădăcina copiei lipite în etapa următoare pe acea frunză.

Așadar, dacă notăm cu dp[i] numărul de noduri de pe nivelul $i$ care la un moment dat au fost frunze în arborele infinit, iar cu nonLeaves[i] numărul de noduri non-frunză de pe nivelul $i$ din arborele dat, atunci răspunsul problemei s-ar calcula așa:

int ans = 0;
for (int j = 0; j <= min(n - 1, d); j++)
    ans += dp[d - j] * nonLeaves[j];

Mai avem de calculat vectorul dp. Pentru asta vom folosi programare dinamică, iar recurența este destul de simplă. Dacă la etapa curentă un nod de pe nivelul $i$ este frunză, atunci la etapa următoare acesta va contribui cu câte leaves[x] frunze pe fiecare nivel $i + x$ Prin leaves[i] am notat numărul de frunze de pe nivelul $i$ din arborele inițial. Dacă nivelul $i$ nu există, leaves[i] este considerat $0$ Recurența este:

Sursă C++

Mai întâi am făcut un DFS pe arborele inițial, calculând pe parcurs vectorii leaves și nonLeaves. Apoi am calculat dinamica și la final răspunsul problemei.

#include <bits/stdc++.h>
using namespace std;

ifstream fin("tairos.in");
ofstream fout("tairos.out");

const int MOD = 1e9 + 7;

int main() {
    int n, d; fin >> n >> d;
    vector<vector<int>> ad(n + 1);
    for (int i = 1; i < n; i++) {
        int x, y; fin >> x >> y;
        ad[x].push_back(y);
        ad[y].push_back(x);
    }

    vector<int> leaves(n + 1);
    vector<int> nonLeaves(n + 1);
    function<void(int, int, int)> dfs = [&](int node, int fath, int dpth) {
        if (ad[node].size() == 1 && ad[node][0] == fath)
            leaves[dpth]++;
        else
            nonLeaves[dpth]++;
        for (int nghb : ad[node])
            if (nghb != fath)
                dfs(nghb, node, dpth + 1);
    };
    dfs(1, 0, 0);

    vector<int> dp(d + 1);
    dp[0] = 1;
    for (int i = 1; i <= d; i++)
        for (int j = 0; j <= min(n - 1, i); j++)
            dp[i] = (dp[i] + 1LL * dp[i - j] * leaves[j]) % MOD;

    int ans = 0;
    for (int j = 0; j <= min(n - 1, d); j++)
        ans = (ans + 1LL * dp[d - j] * nonLeaves[j]) % MOD;
    fout << ans << '\n';
    return 0;
}

Dacă ai vreo nedumerire cu privire la problema Tairos, lasă un comentariu și te voi ajuta