Algoritmul lui Lee în C++ – Problema labirintului

Algoritmul lui Lee reprezintă una dintre cele mai cunoscute aplicații ale cozii (ca structură de date) și este folosit de obicei pentru determinarea drumului minim dintre două celule ale unei matrice. Algoritmul lui Lee există mai mult în folclorul românesc; străinii îl consideră doar un Breadth-First Search pe un caz particular de graf (matricea). Ei prin Algoritmul lui Lee se referă mai degrabă la un algoritm de înfășurătoare convexă, care e cu totul altceva. În acest articol voi prezenta Algoritmul lui Lee, cum se folosește în problema labirintului, precum și câteva aplicații ale acestuia.

Problema labirintului

Se dă un labirint sub forma unei matrice cu $m$ linii și $n$ coloane, unde dacă o celulă este $0$ aceasta se consideră accesibilă de către șoarece, iar dacă este $-1$ inaccesibilă. De asemenea, se dau coordonatele pozițiilor în care se află inițial șoarecele și bucata de brânză.

La fiecare pas, șoarecele se poate deplasa într-una dintre pozițiile imediat vecine la nord, sud, est sau vest, cu condiția ca aceasta să fie accesibilă și, desigur, să se afle în interiorul matricei.

Să se determine lungimea minimă a unui drum de la șoarece la brânză, precum și un astfel drum. Dacă nu se poate ajunge la brânză (este înconjurată de obstacole), se va afișa $0$

Exemplu

Iată matricea corespunzătoare exemplului de mai jos. Am reprezentat cu alb pozițiile accesibile, cu mov pozițiile inaccesibile, cu roșu poziția șoarecelui, iar cu verde poziția brânzei.

Date de intrare

10 10
 0  0  0  0  0 -1  0 -1  0  0
 0  0  0 -1  0 -1  0 -1 -1 -1
-1 -1 -1 -1  0 -1  0  0  0  0
 0  0 -1  0  0  0  0 -1 -1 -1
 0  0 -1  0 -1  0  0  0  0  0
 0  0 -1  0 -1  0  0 -1 -1 -1
 0  0  0  0 -1  0  0  0  0  0
 0  0  0  0 -1  0  0 -1 -1 -1
 0  0 -1  0 -1 -1  0  0  0  0
 0  0 -1  0  0 -1  0  0  0  0
4 1
6 7

Date de ieșire

15
4 1
4 2
5 2
6 2
7 2
7 3
7 4
6 4
5 4
4 4
4 5
4 6
4 7
5 7
6 7

Algoritmul lui Lee

Vom utiliza o matrice $\mathrm{mat}$ cea pe care o citim, și pe care o vom folosi de asemenea pentru a calcula niște rezultate parțiale despre care voi vorbi imediat. Avem nevoie și de o coadă $q$ cu elemente de tip Pos. Tipul Pos va fi un struct pentru reținerea coordonatelor celulelor din matrice. Acesta conține câmpurile $row$ și $col$ pentru linia și coloana poziției stocate.

• În coada $q$ se adaugă poziția șoarecelui.

• Se completează această poziție din $\mathrm{mat}$ cu valoarea $1$

• Cât timp coada nu este vidă și nici nu am găsit lungimea minimă:

  • Extragem primul element din coadă. Să-i zicem $\mathrm{pos}$

  • Îi parcurgem vecinii din matrice:

    • Dacă vecinul curent este accesibil și nevizitat:

      • Îl marcăm drept vizitat, completând celula sa corespunzătoare din $\mathrm{mat}$ cu valoarea $\mathrm{mat}[\mathrm{pos}.row][\mathrm{pos}.col] + 1$
      • Îl introducem în coadă.

• Afișăm valoarea din $\mathrm{mat}$ de pe poziția unde se află bucata de brânză.

Complexitatea algoritmului este $O(m \cdot n)$ deoarece fiecare celulă a matricei este vizitată maxim o singură dată. Această complexitate este optimă, având în vedere dimensiunile input-ului.

Exemplu

Iată cum funcționează completarea matricei $\mathrm{mat}$ de mai sus prin Algoritmul lui Lee. La finalul animației arăt și cum se reconstituie drumul, lucru despre care voi vorbi mai târziu.

Explicația algoritmului

În timpul execuției algoritmului, în matricea $\mathrm{mat}$ o poziție are valoarea $-1$ dacă este inaccesibilă, $0$ dacă încă nu a fost vizitată, sau distanța minimă de la șoarece la ea altfel. Algoritmul lui Lee se bazează pe următoarea idee: Dacă știm lungimea drumului optim de la șoarece până la poziția accesibilă de coordonate $i$ și $j$ $\htmlClass{katexified}{(} \mathrm{mat}[i][j]$ putem actualiza lungimile drumurilor minime pentru vecinii accesibili (și nevizitați încă) ai ei; aceste valori vor fi egale cu $\mathrm{mat}[i][j] + 1$ pentru că de la poziția $(i, j)$ până la un vecin de-al ei se mai face un singur pas. Asta e practic o relație de recurență, motiv pentru care Algoritmul lui Lee poate fi considerat un algoritm de programare dinamică.

Totuși, recurența asta nu e suficientă. Mai trebuie să ținem cont de ordinea în care completăm matricea $\mathrm{mat}$ După ce am completat toate celulele din $\mathrm{mat}$ cu valoarea $x$ (cele până la care se poate ajunge în minim $x$ pași), trebuie să completăm lungimile minime pentru vecinii lor (cu $x + 1$ apoi pentru vecinii vecinilor lor (cu $x + 2$ și tot așa. Doar în acest fel putem fi siguri că toate rezultatele din $\mathrm{mat}$ sunt corecte. Completarea matricei poate fi asemănată cu modul în care o picătură de cerneală se extinde pe o bucată de hârtie.

Pentru a menține această ordine a completării matricei, se folosește o coadă, căci această structură de date funcționează pe principiul primul venit, primul servit. La fiecare pas, din coadă extragem primul element pentru a-l prelucra (a completa lungimile corespunzătoare vecinilor accesibili și a-i adăuga la sfârșitul cozii). Întotdeauna, o parte dintre pozițiile din coadă (primele) vor avea o anumită valoare $k$ iar restul (vecinii lor) vor avea valoarea $k + 1$

Găsirea unui drum optim

Acum că avem matricea $\mathrm{mat}$ completată, putem folosi soluțiile subproblemelor pentru construirea unui drum de lungime minimă de la șoarece $\htmlClass{katexified}{(} beg$ la brânză $\htmlClass{katexified}{(} end$ Asta nu mai ține de Algoritmul lui Lee, dar n-are sens să scriu un alt articol doar pentru această cerință.

Secretul este să pornim de la brânză și să ne îndreptăm spre șoarece, nu invers, cum ar fi fost natural. Știm că dacă un vecin $\mathrm{ngh}$ (de la neighbor – vecin în engleză) al celulei $\mathrm{pos}$ are valoarea $\mathrm{mat}[\mathrm{pos}.row][\mathrm{pos}.col] - 1$ atunci din $\mathrm{ngh}$ sigur se poate ajunge în $\mathrm{pos}$ (într-un singur pas). Cu alte cuvinte, sigur există un drum optim de la șoarece la $\mathrm{pos}$ care trece prin $\mathrm{ngh}$ Dacă porneam de la șoarece n-am fi avut niciodată cum să știm dacă suntem pe drumul bun sau nu. Vă puteți uita la animația de mai sus pentru a (re)vedea cum se reconstituie drumul.

Folosind această idee, putem deduce un algoritm foarte simplu ce rezolvă această cerință. Inițializăm o stivă $\mathrm{st}$ cu poziția unde se află brânza. Căutăm un vecin al acestei celule, care respectă proprietatea de mai sus, și îl adăugăm în stivă. Apoi, repetăm procedeul pentru el. Facem asta până când ajungem la poziția șoarecelui. La final, extragem și afișăm, pe rând, pozițiile din stivă.

Pos pos;
st[++vf] = pos = end;
while (mat[pos.row][pos.col] > 1)
    for (int i = 0; i < 4; i++) {
        Pos ngh; // Explic imediat ce sunt addRow și addCol:
        ngh.row = pos.row + addRow[i];
        ngh.col = pos.col + addCol[i];
        if (mat[ngh.row][ngh.col] == mat[pos.row][pos.col] - 1) {
            st[++vf] = pos = ngh;
            break;
        }
    }
while (vf) {
    fout << st[vf].row << ' ' << st[vf].col << '\n';
    vf--;
}

Din modul în care m-am exprimat este clar că problema se poate rezolva și recursiv, mai simplu. Dacă dimensiunile matricei sunt suficient de mici pentru a nu se produce stack overflow, prefer să folosesc această variantă:

// Se va apela print(end).
void print(Pos pos) {
    if (pos.row == beg.row && pos.col == beg.col) {
        fout << beg.row << ' ' << beg.col << '\n';
        return;
    }
    for (int i = 0; i < 4; i++) {
        Pos ngh;
        ngh.row = pos.row + addRow[i];
        ngh.col = pos.col + addCol[i];
        if (mat[ngh.row][ngh.col] == mat[pos.row][pos.col] - 1) {
            print(ngh);
            fout << pos.row << ' ' << pos.col << '\n';
            return;
        }
    }
}

Implementare în C++

Până la prezentarea celor două surse C++ propuse, trebuie să mai discutăm despre niște detalii legate de implementare.

Bordarea matricei

Bordarea matricei este o tehnică des folosită în problemele cu matrice. Aceasta presupune să înconjurăm (să bordăm) matricea propriu-zisă cu un anumit număr. Pentru ca bordarea să fie efectuată corect, trebuie să avem grijă la declararea dimensiunilor maxime ale matricei. Aceasta trebuie să fie declarată cu măcar două linii și două coloane în plus. De asemenea, este necesar să poziționăm colțul din stânga-sus al matricei în $(1, 1)$ pentru a lăsa loc bordurii să treacă prin $(0, 0)$

Putem folosi ideea asta și în problema noastră. Ca să verificăm dacă poziția $\mathrm{pos}$ se află în interiorul matricei propriu-zise, ar trebui să efectuăm de fiecare dată aceste teste enervante:

if (1 <= pos.row && pos.row <= m &&
    1 <= pos.col && pos.col <= n)

Pe lângă faptul că face codul mai complicat, nici nu este eficient, pentru că s-ar executa de foarte multe ori. Însă, putem borda inițial matricea cu valoarea $-1$ ca și cum ar fi înconjurată de obstacole. Astfel, nu vom ieși niciodată din matrice, pentru că asta ar însemna să ne expandăm în celule inaccesibile.

Iată implementarea scurtă și simplă a bordării matricei $\mathrm{mat}$

// Vertical:
for (int i = 0; i <= m + 1; i++)
    mat[i][0] = mat[i][n + 1] = -1;
// Orizontal:
for (int j = 0; j <= n + 1; j++)
    mat[0][j] = mat[m + 1][j] = -1;

Vectorii de deplasare

Ar fi aiurea să parcurgem vecinii unei poziții ca mai jos, pentru că am scrie de patru ori aceleași operații:

prelucrare(mat[pos.row - 1][pos.col]);
prelucrare(mat[pos.row][pos.col + 1]);
prelucrare(mat[pos.row + 1][pos.col]);
prelucrare(mat[pos.row][pos.col - 1]);

Ar fi frumos să putem parcurge vecinii cu un for. Ei bine, putem face asta dacă declarăm mai întâi vectorii de deplasare:

const int addRow[] = {-1, 0, 1,  0};
const int addCol[] = { 0, 1, 0, -1};

Acești vectori conțin pe poziția $i$ niște valori care, adunate la coordonatele celulei curente, conduc la obținerea coordonatelor celui de-al $i$lea vecin al ei:

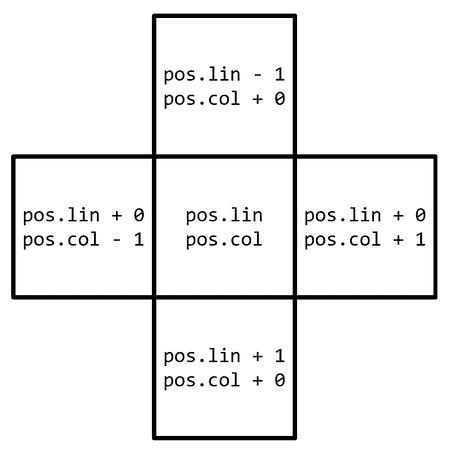
Nu avem decât să ne folosim de acești vectori pentru a inițializa o variabilă $\mathrm{ngh}$ ce reține coordonatele vecinului curent, pe care să o folosim în continuare.

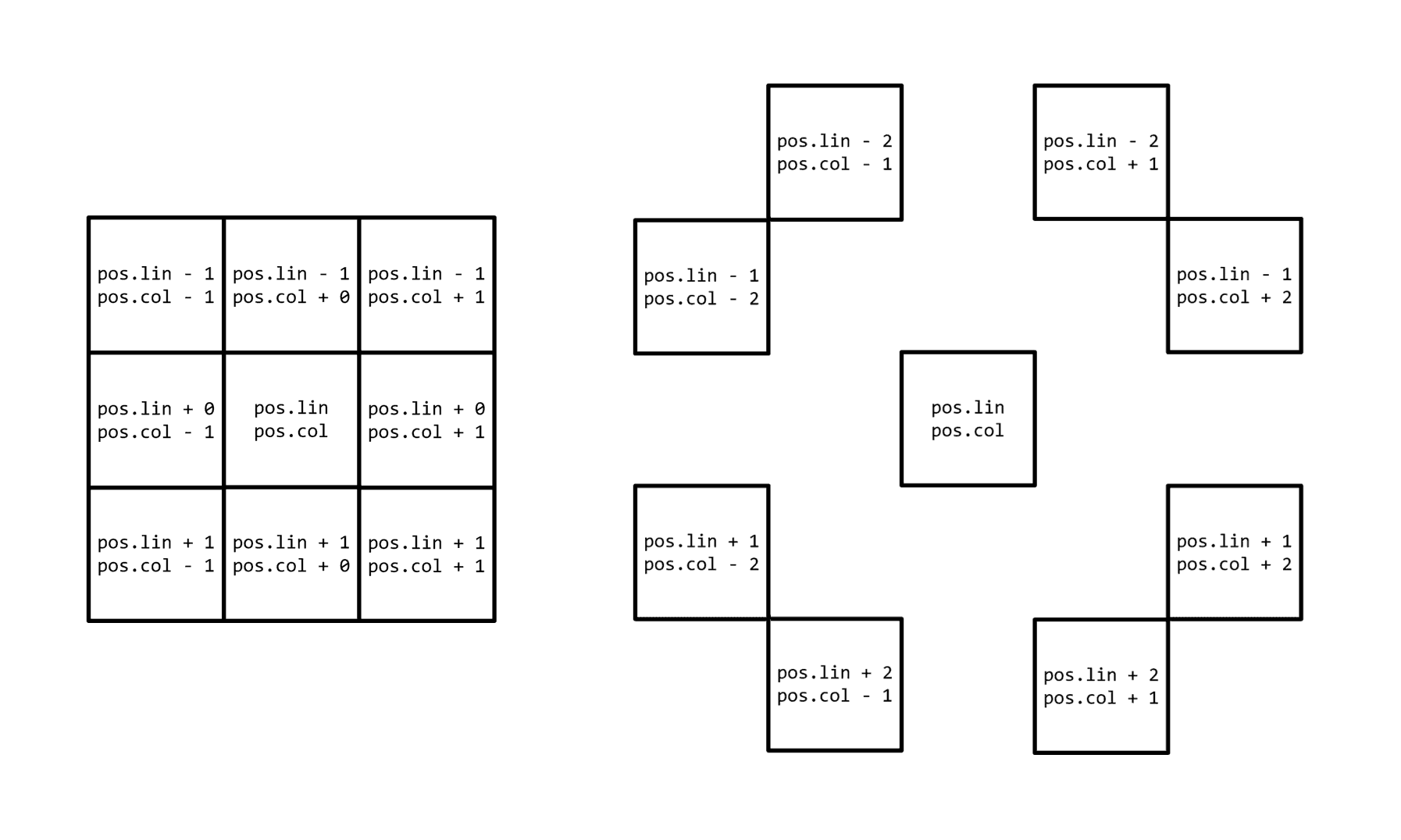
for (int i = 0; i < 4; i++) {
    Pos ngh;
    ngh.row = pos.row + addRow[i];
    ngh.col = pos.col + addCol[i];
    // ...
}

Iată cum arată coordonatele vecinilor lui $\mathrm{pos}$ în cazul în care deplasarea se făcea cu o unitate pe $8$ direcții, precum și în cazul în care deplasarea se făcea similar cu cea a calului de pe o tablă de șah:

Sursele C++

Prima sursă este cea clasică, ce folosește o coadă implementată sub forma unui vector static și găsește drumul optim iterativ. A doua sursă este una scrisă în spiritul C++17. Folosește STL pentru coadă și construiește drumul recursiv. Sper că eleganța acestei variante vă va încuraja să scrieți și voi cod după noile standarde

#include <fstream>
using namespace std;
const int DMAX = 618;

ifstream fin("lee.in");
ofstream fout("lee.out");

const int addRow[] = {-1, 0, 1, 0};
const int addCol[] = {0, 1, 0, -1};

struct Pos {
    int row;
    int col;
};

int m, n;
int mat[DMAX][DMAX];
Pos beg, end;

int in, sf;
Pos q[DMAX * DMAX];

int vf;
Pos st[DMAX * DMAX];

void scan() {
    fin >> m >> n;
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            fin >> mat[i][j];
    fin >> beg.row >> beg.col;
    fin >> end.row >> end.col;
}

void surround() {
    for (int i = 0; i <= m + 1; i++) mat[i][0] = mat[i][n + 1] = -1;
    for (int j = 0; j <= n + 1; j++) mat[0][j] = mat[m + 1][j] = -1;
}

void lee() {
    q[0] = beg;
    in = sf = 0;
    mat[beg.row][beg.col] = 1;
    Pos pos;
    while (in <= sf && !mat[end.row][end.col]) {
        pos = q[in++];
        for (int i = 0; i < 4; i++) {
            Pos ngh;
            ngh.row = pos.row + addRow[i];
            ngh.col = pos.col + addCol[i];
            if (!mat[ngh.row][ngh.col]) {
                mat[ngh.row][ngh.col] = mat[pos.row][pos.col] + 1;
                q[++sf] = ngh;
            }
        }
    }
}

void print() {
    Pos pos = st[++vf] = end;
    while (mat[pos.row][pos.col] > 1)
        for (int i = 0; i < 4; i++) {
            Pos ngh;
            ngh.row = pos.row + addRow[i];
            ngh.col = pos.col + addCol[i];
            if (mat[ngh.row][ngh.col] == mat[pos.row][pos.col] - 1) {
                st[++vf] = pos = ngh;
                break;
            }
        }
    fout << mat[end.row][end.col] << '\n';
    while (vf) {
        fout << st[vf].row << ' ' << st[vf].col << '\n';
        vf--;
    }
}

int main() {
    scan();
    surround();
    lee();
    print();
    return 0;
}

Aplicații ale algoritmului

În această problemă, ne-am putut opri din completarea matricei imediat după ce am ajuns la brânză. Adesea însă, este util să lăsăm algoritmul să ruleze până se umple toată matricea. Iată ideile de rezolvare a trei probleme de pe .campion și InfoArena cu Algoritmul lui Lee:

• Rj. Facem două Lee-uri: unul din poziția lui Romeo și unul din poziția Julietei. Apoi, parcurgem simultan cele două matrice obținute. Când găsim o poziție pentru care valorile din ambele matrice sunt egale, înseamnă că cei doi pot ajunge acolo simultan. Mai rămâne să determinăm o astfel de poziție cu valoare minimă, pentru că numărul de pași trebuie să fie minim.

• șoricel3. Pentru calcularea gradelor de periculozitate din întreaga matrice, inițializăm punctele de pândă cu $m + n$ Le introducem pe toate în coadă, și începem Lee-ul, expandându-ne simultan din toate punctele de pândă. Valorile vor scădea din $1$ în $1$ în loc să crească. Pentru determinarea drumului minim, vom înlocui coada din Lee-ul clasic cu o coadă de priorități. La fiecare pas, vom extrage cel mai mic element din coadă, pentru că dorim să ne extindem mai întâi în zone cât mai sigure. În plus, rezultatele subproblemelor vor fi gradele de periculozitate ale drumurilor, nu lungimile lor. Tehnica aceasta se numește Algoritmul lui Lee cu costuri. Este asemănător cu Algoritmul lui Dijkstra, doar că graful (matricea) are costuri pe noduri, nu pe muchii.

• Rover. Prima cerință este tot o variație a algoritmului lui Lee. De data aceasta, coada se înlocuiește cu un deque. Am explicat pe larg cum se rezolvă problema asta în acest articol.

Asta e tot ce am avut de spus despre Algoritmul lui Lee și problema labirintului. Dacă aveți vreo întrebare despre Algoritmul lui Lee, sau nu ați înțeles vreun detaliu din acest articol, nu ezitați să lăsați un comentariu mai jos