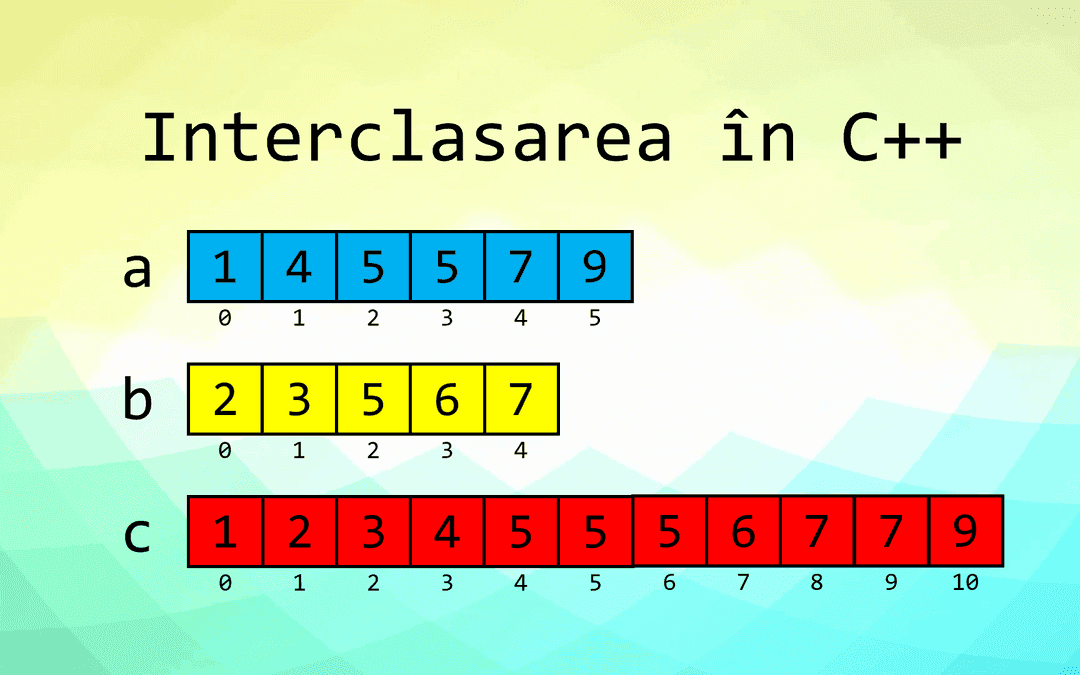
Interclasarea a doi vectori în C++. Operații pe mulțimi

Fiind dați doi vectori sortați, prin interclasarea lor se înțelege construirea unui al treilea vector sortat care să conțină toate elementele acestora. Printre cele mai importante aplicații ale interclasării se numără reuniunea și intersecția a două mulțimi, dar mai ales sortarea prin interclasare. În acest articol voi prezenta implementarea algoritmului de interclasare în C++, și de asemenea cum poate fi modificat acesta pentru a calcula reuniunea și intersecția a două mulțimi.

În continuare, vom considera că vrem să interclasăm vectorii $a$ de lungime $m$ și $b$ de lungime $n$ formând un vector $c$ de lungime $p$ Toți vectorii vor fi indexați de la $0$

Exemplu

Soluții naive

Printre primele soluții care ne vin în minte se regăsesc:

a) Copiem tot vectorul $a$ în $c$ iar apoi luăm pe rând elementele lui $b$ și le inserăm pe pozițiile lor corespunzătoare în $c$ Mai precis, parcurgem de la dreapta la stânga vectorul $c$ cât timp elementele sale sunt mai mici decât elementul curent din $b$ timp în care le mutăm cu o poziție la dreapta, pentru a-i face loc elementului nou. Procedeul este similar sortării prin inserție. Complexitatea algoritmului este $O(m \cdot n)$

p = m;
for (int i = 0; i < m; i++)
    c[i] = a[i];
for (int j = 0; j < n; j++, p++)
    for (int i = p - 1; i >= 0; i--)
        if (c[i] > b[j])
            c[i + 1] = c[i];
        else {
            c[i + 1] = b[j];
            break;
        }

b) Concatenăm cei doi vectori în $c$ (introducem în $c$ elementele lui $a$ iar în continuare elementele lui $b$ și apoi sortăm vectorul $c$ Complexitatea diferă în funcție de algoritmul de sortare ales, dar în cel mai bun caz este $O((m + n) \cdot \log (m + n))$

p = m + n;
for (int i = 0; i < m; i++)
    c[i] = a[i];
for (int j = 0; j < n; j++)
    c[m + j] = b[j];
sort(c, c + p);

c) Dacă intervalul de valori este suficient de mic, putem lua un vector de frecvență în care să reținem de câte ori apare în cei doi vectori fiecare element din acel interval, și apoi să-l parcurgem inserând în $c$ elementele corespunzătoare, similar sortării prin numărare. Timpul de rulare al algoritmului are complexitatea $O(m + n + lg)$ unde $lg$ este lungimea intervalului.

for (int i = 0; i < m; i++)
    frq[a[i]]++;
for (int j = 0; j < n; j++)
    frq[b[j]]++;
for (int i = MIN; i <= MAX; i++)
    while (frq[i]--)
        c[p++] = i;

Interclasare în $O(m + n)$

Totuși, soluțiile de mai sus nu prea se folosesc de faptul că vectorii $a$ și $b$ sunt deja sortați. Ei bine, privind problema recursiv, putem deduce destul de ușor algoritmul optim de interclasare: Pentru a interclasa secvențele $a[i, m)$ și $b[j, n)$ trebuie mai întâi să inserăm în $c$ minimul dintre $a[i]$ și $b[j]$ iar apoi să interclasăm secvențele rămase. Acestea sunt $a[i + 1, m)$ și $b[j, n)$ în cazul în care $a[i] \lt b[j]$ sau $a[i, m)$ și $b[j + 1, n)$ în caz contrar. Nu este nevoie să tratăm separat cazul $a[i] = b[j]$ deoarece nu are importanță pe care îl vom insera primul în $c$

Așadar, algoritmul iterativ (ce se folosește în principal de o structură repetitivă) sună astfel:

• Reținem în $i$ poziția curentă din $a$ iar în $j$ poziția curentă din $b$ Inițializăm $i$ și $j$ cu $0$ Reținem de asemenea în $p$ lungimea curentă a lui $c$ care inițial este $0$

• Parcurgem simultan cei doi vectori, cât timp $i \lt m$ și $j \lt n$

  • Dacă $a[i] \lt b[j]$ atunci $c[p]$ devine $a[i]$ și îi incrementăm pe $i$ și $p$
  • Altfel, $c[p]$ devine $b[j]$ și îi incrementăm pe $j$ și $p$

• Inserăm în $c$ elementele rămase din $a$

• Inserăm în $c$ elementele rămase din $b$

Iată o animație făcută de mine care ilustrează modul în care lucrează acest algoritm pe vectorii din exemplu:

Mai jos puteți vedea implementarea algoritmului în C++:

int i = 0, j = 0;
while (i < m && j < n)
    if (a[i] < b[j])
        c[p++] = a[i++];
    else
        c[p++] = b[j++];
while (i < m)
    c[p++] = a[i++];
while (j < n)
    c[p++] = b[j++];

Se observă că după primul while, într-un vector întotdeauna vor mai rămâne elemente de inserat în $c$ Prin urmare, doar unul dintre următoarele două while-uri se va executa. Complexitatea algoritmului este $O(m + n)$ deoarece fiecare element din $a$ și $b$ va fi folosit o singură dată.

O implementare mai elegantă

Implementarea pe care urmează să o prezint este la fel de eficientă ca cea precedentă, însă e mai drăguță și ceva mai scurtă. Ideea este să adăugăm la vectorii $a$ și $b$ o valoare $\mathrm{INF}$ mai mare decât numărul maxim care se poate afla inițial în ei (o santinelă). Astfel, pentru primul while este suficientă condiția i < m || j < n, și nu vom mai avea nevoie de celelalte două while-uri: Când s-au terminat elementele dintr-un vector, valorile din celălalt vor fi comparate cu $\mathrm{INF}$ care sigur e mai mare decât ele.

Iată mai jos o sursă C++ completă, ce cuprinde citirea, interclasarea și afișarea vectorilor. Drept $\mathrm{INF}$ am folosit constanta 1e9, care este egală cu $10^9$

#include <bits/stdc++.h>
using namespace std;

const int INF = 1e9;
const int VMAX = 618;

int m, a[VMAX];
int n, b[VMAX];
int p, c[2 * VMAX];

int main() {
    cin >> m; a[m] = INF;
    for (int i = 0; i < m; i++)
        cin >> a[i];

    cin >> n; b[n] = INF;
    for (int j = 0; j < n; j++)
        cin >> b[j];

    int i = 0, j = 0;
    while (i < m || j < n)
        if (a[i] < b[j])
            c[p++] = a[i++];
        else
            c[p++] = b[j++];

    for (int i = 0; i < p; i++)
        cout << c[i] << ' ';
    cout << '\n';
    return 0;
}

Reuniunea și intersecția a două mulțimi prin interclasare

O aplicație importantă a interclasării este efectuarea operațiilor de reuniune și intersecție a două mulțimi. În continuare, vom considera că cele două mulțimi date sunt chiar vectorii $a$ și $b$ cu condiția suplimentară că fiecare dintre aceștia are toate elementele distincte două câte două. Mulțimea-rezultat se va afla în vectorul $c$

Modificările pe care trebuie să i le aducem algoritmului de interclasare pentru a obține reuniunea și respectiv intersecția a două mulțimi sunt: Pentru reuniune, când $a[i] = b[j]$ vom avansa în ambii vectori, ca să nu introducem de două ori aceeași valoare în $c$

int i = 0, j = 0;
while (i < m || j < n)
    if (a[i] < b[j])
        c[p++] = a[i++];
    else if (a[i] > b[j])
        c[p++] = b[j++];
    else {
        c[p++] = a[i];
        i++; j++;
    }

Pentru intersecție, introducem elemente în $c$ doar atunci când $a[i] = b[j]$ pentru că celelalte (până la pasul respectiv) nu se regăsesc în ambii vectori.

int i = 0, j = 0;
while (i < m || j < n)
    if (a[i] < b[j])
        i++;
    else if (a[i] > b[j])
        j++;
    else {
        c[p++] = a[i];
        i++; j++;
    }

O altă aplicație importantă a interclasării este sortarea prin interclasare (Merge Sort), dar despre ea voi discuta în alt articol. Dacă aveți vreo întrebare legată de algoritmul de interclasare în C++, nu ezitați să o adresați mai jos, în rubrica de comentarii