Problema 2șah – OJI 2015, Clasa a 11-a

• Dificultate:
• Autor: Adrian Panaete
• Online: InfoArena, PbInfo

Rezumat

Se dă o tablă de șah cu $n + 1$ linii și $2n + 1$ coloane, construită după modelul de mai jos:

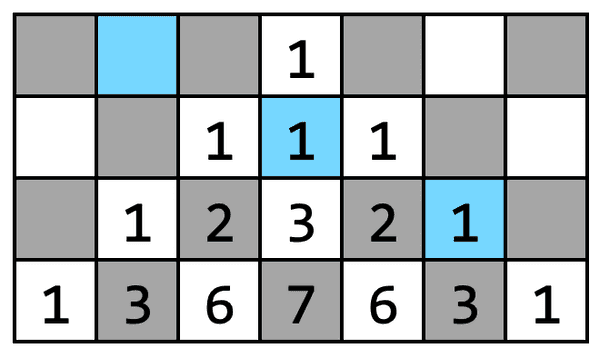
Pe prima linie, elementul de pe poziția $n + 1$ este $1$ iar restul sunt $0$ Începând cu a doua linie, fiecare element $(i, j)$ este suma elementelor $(i - 1, j - 1)$ $(i - 1, j)$ și $(i - 1, j + 1)$

Un cal pleacă din poziția $(1, k)$ cu $k \le n$ sărind la fiecare pas din poziția $(i, j)$ în poziția $(i + 1, j + 2)$ atât timp cât este posibil. În exemplul de mai sus, calul pleacă din $(1, 2)$ și trece prin celulele colorate cu albastru. Cunoscând $n$ și $k$ să se determine:

1. Suma numerelor de pe linia $k$ a matricei.
2. Suma numerelor din celulele prin care trece calul.

Răspunsul fiecărei cerințe va fi calculat modulo $100\,003$

Soluție

Pentru prima cerință se observă imediat că răspunsul este $3^{k - 1}$ Asta deoarece pe prima linie suma este $3^0$ iar fiecare element $(i, j)$ din matrice contribuie la valoarea a trei elemente de pe linia următoare: $(i + 1, j - 1)$ $(i + 1, j)$ și $(i + 1, j + 1)$ de unde suma de pe linia $i + 1$ este de trei ori suma de pe linia $i$ Cum $n$ poate fi foarte mare, va trebui să calculăm această putere folosind exponențiere logaritmică.

Pentru a doua cerință, observăm că putem reduce numărul de parametri ai problemei de la doi $\htmlClass{katexified}{(} n$ și $k$ la unul singur – distanța poziției inițiale a calului față de vârful piramidei, adică $n - k$ De exemplu, atât pentru $n = 4, k = 1$ cât și pentru $n = 6, k = 3$ traseul calului este același. Sau cel puțin partea traseului care intersectează piramida.

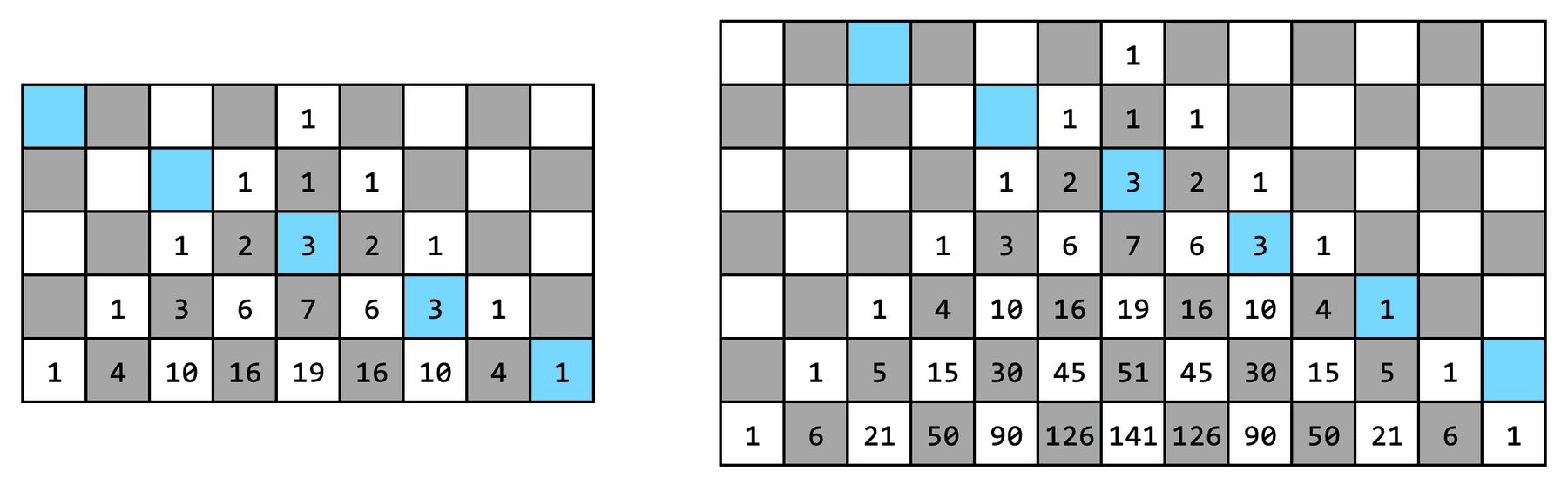
Acum, să vedem ce răspunsuri obținem pentru diferite valori ale lui $n - k$

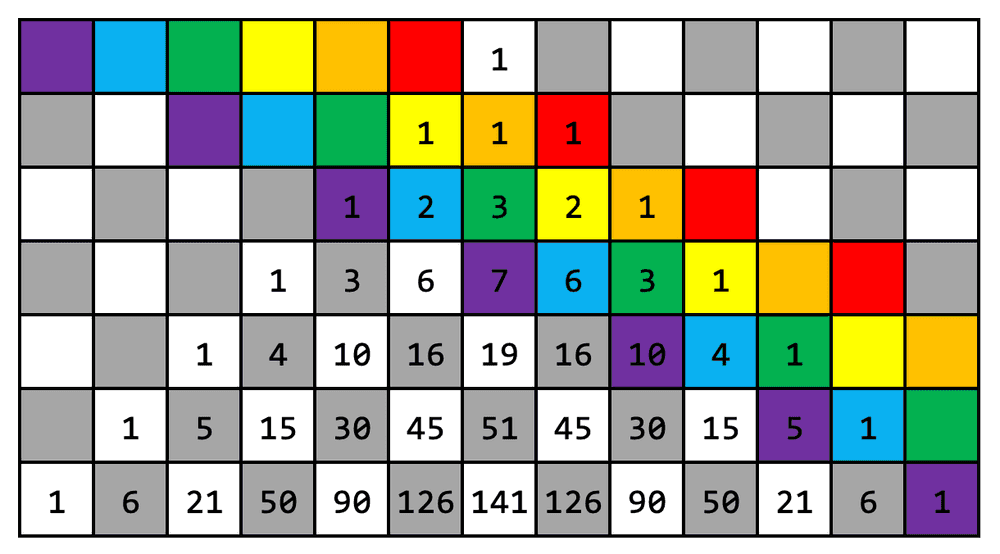
• Pentru $n - k = 0$ (traseul roșu) suma este $1$
• Pentru $n - k = 1$ (traseul portocaliu) suma este $2$
• Pentru $n - k = 2$ (traseul galben) suma este $4$
• Pentru $n - k = 3$ (traseul verde) suma este $7$
• Pentru $n - k = 4$ (traseul albastru) suma este $13$
• Pentru $n - k = 5$ (traseul mov) suma este $24$

Deja se conturează o recurență foarte simplă:

Dacă vrem să o și demonstrăm, trebuie să ne uităm mai atent la desen:

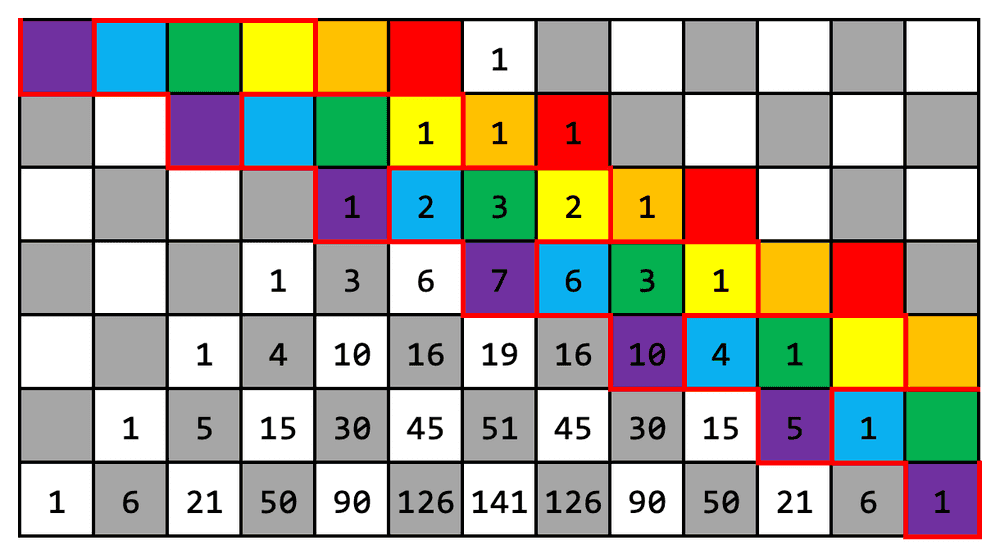
Să luăm de exemplu traseul mov. Fiecare element al său este suma celor trei elemente de deasupra acestuia – unul albastru, unul verde și unul galben. Deci, știm că fiecare element mov este „format” din unul albastru, unul verde și unul galben, dar și că fiecare element albastru, verde sau galben contribuie la exact unul mov. De aici, suma de pe traseul mov este egală cu suma de pe cel albastru plus suma de pe cel verde plus suma de pe cel galben. Generalizând, obținem $\mathrm{dp}[i] = \mathrm{dp}[i - 1] + \mathrm{dp}[i - 2] + \mathrm{dp}[i - 3]$ pentru $i \ge 3$ Răspunsul problemei este $\mathrm{dp}[n - k]$

Din nou, $n$ poate fi foarte mare, așa că pentru a calcula această recurență trebuie să folosim exponențiere logaritmică pe matrice. Am explicat pe larg această tehnică aici. Vom folosi următoarea formulă:

Sursă C++

#include <bits/stdc++.h>
using namespace std;

ifstream fin("2sah.in");
ofstream fout("2sah.out");

const int MOD = 100003;

class Matrix {
    int n;
    vector<vector<int>> mat;

public:
    Matrix(int n) : n(n), mat(n, vector<int>(n)) { }
    vector<int>& operator[](int ind) { return mat[ind]; }

    static Matrix null(int n) {
        Matrix ret(n);
        for (int i = 0; i < n; i++)
            ret[i][i] = 1;
        return ret;
    }

    friend Matrix operator*(Matrix x, Matrix y);
    friend vector<int> operator*(Matrix x, vector<int> y);
    friend Matrix pwr(Matrix x, int y);
};

Matrix operator*(Matrix x, Matrix y) {
    Matrix ret(x.n);
    for (int i = 0; i < x.n; i++)
        for (int j = 0; j < x.n; j++)
            for (int k = 0; k < x.n; k++)
                ret[i][j] = (ret[i][j] + 1LL * x[i][k] * y[k][j]) % MOD;
    return ret;
}

vector<int> operator*(Matrix x, vector<int> y) {
    vector<int> ret(x.n);
    for (int i = 0; i < x.n; i++)
        for (int k = 0; k < x.n; k++)
            ret[i] = (ret[i] + 1LL * x[i][k] * y[k]) % MOD;
    return ret;
}

Matrix pwr(Matrix x, int y) {
    if (!y)
        return Matrix::null(x.n);
    if (y % 2)
        return x * pwr(x * x, y / 2);
    return pwr(x * x, y / 2);
}

int pwr(int x, int n) {
    if (!n)
        return 1;
    if (n % 2)
        return 1LL * x * pwr(1LL * x * x % MOD, n / 2) % MOD;
    return pwr(1LL * x * x % MOD, n / 2);
}

int main() {
    int t, n, k; fin >> t >> n >> k;
    if (t == 1)
        fout << pwr(3, k - 1) << '\n';
    else if (n - k == 0)
        fout << "1\n";
    else if (n - k == 1)
        fout << "2\n";
    else {
        vector<int> vec = {1, 2, 4};
        Matrix mat(3);
        mat[0][0] = 0; mat[0][1] = 1; mat[0][2] = 0;
        mat[1][0] = 0; mat[1][1] = 0; mat[1][2] = 1;
        mat[2][0] = 1; mat[2][1] = 1; mat[2][2] = 1;
        fout << (pwr(mat, n - k - 2) * vec)[2] << '\n';
    }
    return 0;
}

Dacă ai vreo nedumerire cu privire la problema 2șah, lasă un comentariu și te voi ajuta