Problema Rufe – OJI 2019, Clasa a 11-a

• Dificultate:
• Autor: Bogdan Ciobanu
• Online: InfoArena, PbInfo

Rezumat

Se dă o matrice cu $m$ linii și $n$ coloane. Alex pune la uscat o șosetă și $k$ tricouri. Începe prin a pune la uscat șoseta în poziția $(a, b)$ Apoi, pune pe rând fiecare dintre cele $k$ tricouri într-o poziție liberă, cât mai îndepărtată de șosetă. Pentru măsurători se folosește distanța Manhattan, ceea ce înseamnă că distanța dintre două celule $(x_1, y_1)$ și $(x_2, y_2)$ se consideră $|x_1 - x_2| + |y_1 - y_2|$ Să se determine distanța dintre poziția șosetei și poziția unde a fost atârnat al $k$lea tricou.

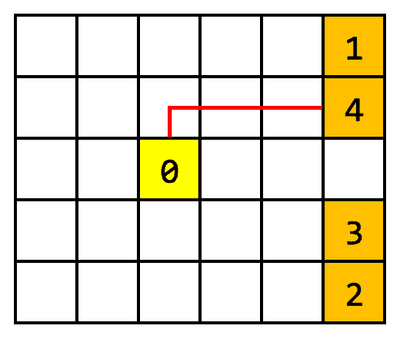
În exemplul de mai sus, $a = b = 3$ iar distanța dintre al patrulea tricou și șosetă este $4$ Ordinea în care sunt așezate tricourile nu este unică. Însă ordinea distanțelor dintre tricouri și șosetă este unică: $5, 5, 4, 4$

Soluție

Se observă ușor că putem căuta binar rezultatul: Cu cât distanța maximă $d$ dintre o celulă nevizitată și $(a, b)$ este mai mică, cu atât am vizitat mai multe celule. Noi vrem să găsim distanța $d$ maximă pentru care am vizitat strict mai puțin decât $k$ celule. Aceea va fi distanța la care va fi plasat al $k$lea tricou. Deci, dacă putem calcula eficient (preferabil în $O(1)$ numărul de celule aflate la distanța maximă $d$ de șosetă, putem răspunde în timp logaritmic printr-un algoritm de genul:

int64_t lo = 0, hi = m + n;
while (hi - lo > 1) {
   int64_t md = (lo + hi) / 2;
   if (m * n - getArea(md) < k)
       hi = md;
   else
       lo = md;
}
fout << hi << '\n';

Rămâne să vedem cum calculăm acel număr de celule. În primul rând, este bine de știut că mulțimea celulelor aflate la distanță Manhattan mai mică sau egală cu $d$ de o anumită celulă $(a, b)$ formează un romb de diagonală $2d + 1$ Iată rombul pentru $d = 6$ și $(a, b) = (2, 3)$

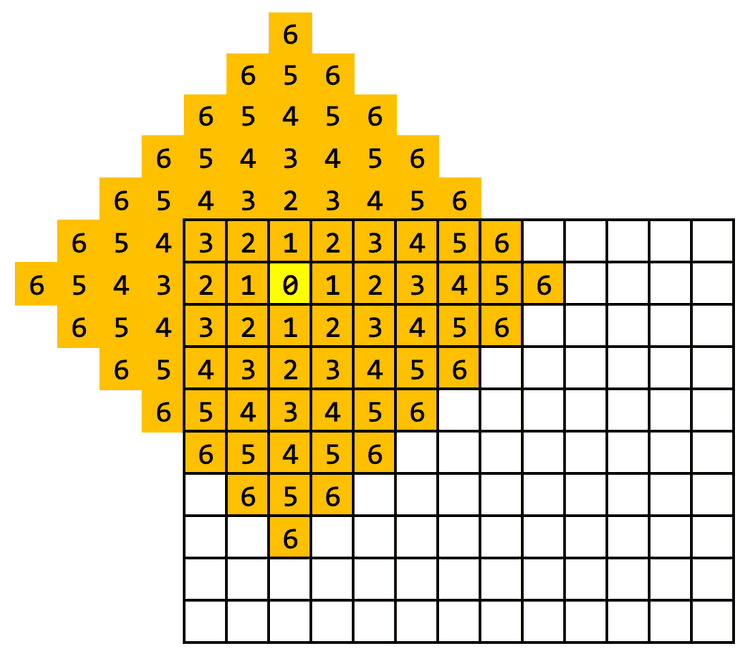
Problema este că rombul poate ieși din matrice, așa că trebuie să avem grijă cum eliminăm celulele din romb care se află în afara matricei. Cum fiecare dintre cele patru colțuri ale rombului poate ieși sau nu din matrice, avem de tratat șaisprezece cazuri. Iar la fiecare este destul de mult de scris și de gândit, motiv pentru care la OJI am rămas cu o sursă nefinalizată, care nici nu știu cum de a reușit să scoată patru puncte.

Aria rombului

Dacă privim problema dintr-o altă perspectivă, inspirată din principiul includerii și excluderii, vom realiza că putem trata intersecțiile independent, obținând opt cazuri mult mai simple. Algoritmul sună cam așa:

• Inițializăm aria rombului ca și cum acesta nu ar ieși deloc din matrice.
• Dacă vârful de sus al rombului iese din matrice, scădem aria triunghiului rezultat.
• Dacă vârful de jos al rombului iese din matrice, scădem aria triunghiului rezultat.
• Dacă vârful din stânga al rombului iese din matrice, scădem aria triunghiului rezultat.
• Dacă vârful din dreapta al rombului iese din matrice, scădem aria triunghiului rezultat.
• Dacă atât vârful de sus cât și cel din stânga ies din matrice, adunăm aria triunghiului rezultat.
• Dacă atât vârful de sus cât și cel din dreapta ies din matrice, adunăm aria triunghiului rezultat.
• Dacă atât vârful de jos cât și cel din stânga ies din matrice, adunăm aria triunghiului rezultat.
• Dacă atât vârful de jos cât și cel din dreapta ies din matrice, adunăm aria triunghiului rezultat.

Să notăm cu $f(n)$ suma primelor $n$ numere naturale, iar cu $g(n)$ suma primelor numere naturale impare mai mici sau egale cu $n$ (care va fi mereu impar). Aceste funcții se calculează după formulele de mai jos, și ne vor ajuta să calculăm ariile triunghiurilor:

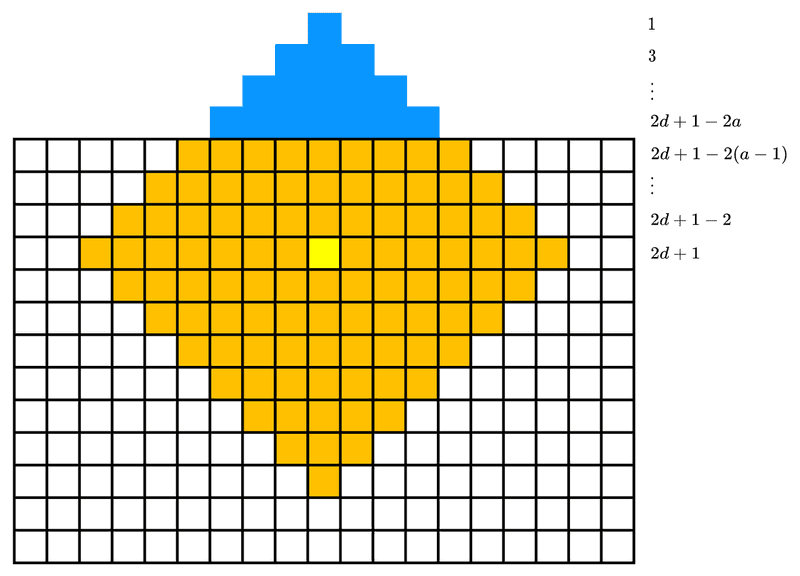
Suma inițială se calculează ușor – împărțim rombul în două triunghiuri plus linia pe care se află centrul. Obținem $2g(2d - 1) + 2d + 1$

Colțul de sus al rombului iese din matrice dacă $a - d \lt 1$ În acest caz, aria triunghiului rezultat este $g(2d + 1 - 2a)$ Analog pentru următoarele trei cazuri.

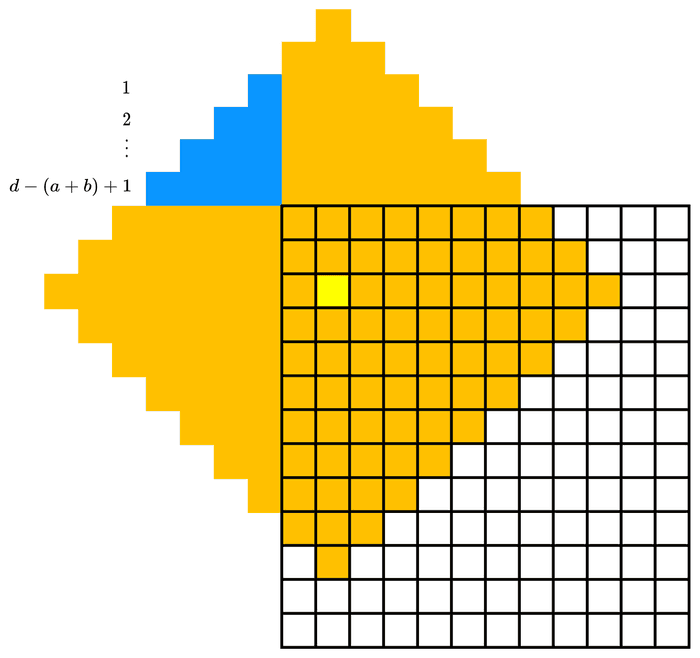
Atât colțul de sus cât și cel din stânga ies din matrice dacă $d \ge a + b$ În acest caz, aria triunghiului rezultat este $f(d - (a + b) + 1)$ Analog pentru următoarele trei cazuri.

Sursă C++

#include <bits/stdc++.h>
using namespace std;

ifstream fin("rufe.in");
ofstream fout("rufe.out");

int64_t sumAll(int64_t n) {
   return n * (n + 1) / 2;
}

int64_t sumOdd(int64_t n) {
   return sumAll(n + 1) - 2 * sumAll((n + 1) / 2);
}

int main() {
   int64_t m, n, a, b, k;
   fin >> m >> n >> a >> b >> k;

   auto getArea = [&](int64_t len) {
       int64_t area = 2 * sumOdd(2 * len - 1) + 2 * len + 1;
       if (a - len < 1) area -= sumOdd(2 * len + 1 - 2 * a);
       if (a + len > m) area -= sumOdd(2 * len + 1 - 2 * (m - a + 1));
       if (b - len < 1) area -= sumOdd(2 * len + 1 - 2 * b);
       if (b + len > n) area -= sumOdd(2 * len + 1 - 2 * (n - b + 1));

       if (len >= a + b) area += sumAll(len - (a + b) + 1);
       if (len >= a + n - b + 1) area += sumAll(len - (a + n - b + 1) + 1);
       if (len >= m - a + 1 + b) area += sumAll(len - (m - a + 1 + b) + 1);
       if (len >= m - a + 1 + n - b + 1) area += sumAll(len - (m - a + 1 + n - b + 1) + 1);
       return area;
   };

   int64_t lo = 0, hi = m + n;
   while (hi - lo > 1) {
       int64_t md = (lo + hi) / 2;
       if (m * n - getArea(md) < k)
           hi = md;
       else
           lo = md;
   }
   fout << hi << '\n';
   return 0;
}

Dacă ai vreo nedumerire cu privire la problema Rufe, lasă un comentariu și te voi ajuta