
Reprezentarea grafurilor în C++
Într-un articol mai vechi am discutat despre noțiunile de bază ale teoriei grafurilor. Acum se pune problema următoare: Cum putem reprezenta eficient un graf în C++? Altfel spus, cum putem reține informațiile necesare pentru prelucrarea unui graf? Voi analiza cele mai cunoscute trei metode: lista de muchii, matricea de adiacență și listele de adiacență.
Reprezentarea grafurilor prin lista de muchii
O soluție naivă este să reținem o listă cu toate muchiile (sau arcele) grafului. Pentru asta, putem folosi o matrice cu două coloane astfel: și ar fi extremitățile muchiei Dacă există costuri pe muchiile grafului, le putem reține adăugând încă o coloană la matrice: ar fi costul muchiei
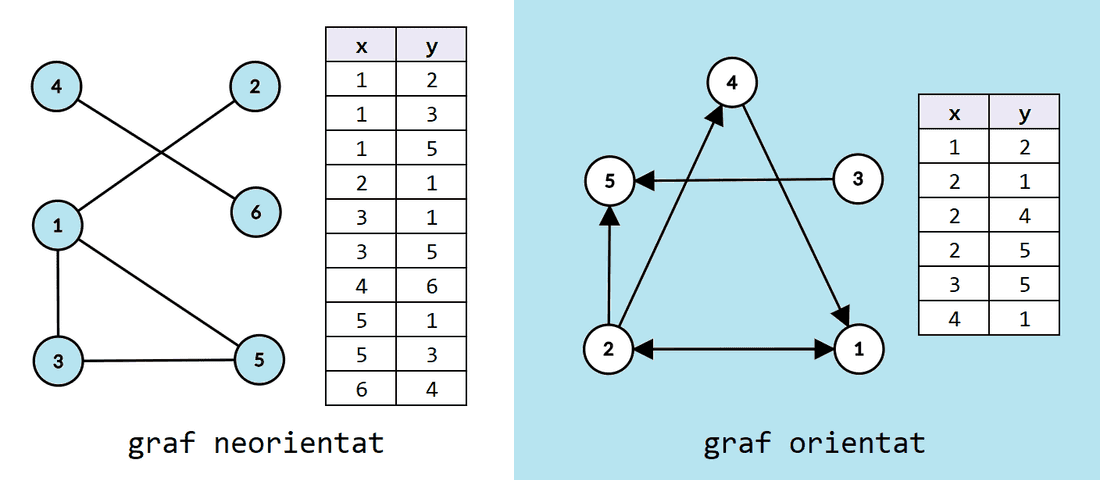
Totuși, ar fi mai elegant să definim un struct numit Edge (muchie în engleză) care să rețină informațiile aferente unei muchii. Deci, pentru stocarea muchiilor vom reține un vector cu elemente de tipul Edge.
struct Edge { int x, y; // extremitățile Edge(int x = 0, int y = 0) { // constructor this->x = x; this->y = y; }};Am definit și un constructor ce primește ca parametri două numere cu care inițializează extremitățile muchiei curente. M-am săturat să primesc warning-uri pentru expresii de genul {x, y}, așa că le-am înlocuit cu Edge(x, y). Aceasta returnează un nou obiect de tipul Edge, construit folosind constructorul de mai sus.
Acum urmează să vedem cum putem efectua operații obișnuite legate de muchii folosind acest mod de reprezentare. Este vorba de accesarea, ștergerea și inserarea unei muchii noi, precum și despre parcurgerea vecinilor unui nod.
Accesarea unei muchii
Pentru a accesa o muchie, sau a verifica dacă aceasta există, trebuie să o căutăm în vector. Complexitatea este deoarece vectorul nu este sortat după niciun criteriu. Nu are sens să ținem vectorul sortat ca să efectuăm căutare binară, pentru că inserarea și ștergerea unei muchii se vor efectua tot în timp liniar. Optimizările ce folosesc căutare binară depind foarte mult de numărul de operații de fiecare tip pe care trebuie să le efectuăm în problemă. Noi vom considera cazul general, cel mai ușor de implementat.
Ștergerea unei muchii
Pentru a șterge o muchie, putem căuta muchia respectivă în vector și să mutăm cu o poziție la stânga toate elementele care o succed. Complexitatea ar fi cu constanta Dar, putem efectua ștergerea efectivă a muchiei în interschimbând-o cu ultima muchie din listă, și decrementând ul direct. Astfel, parcurgem lista o singură dată.
Inserarea unei muchii
Pentru a insera o muchie, o adăugăm pur și simplu la vector, iar apoi incrementăm ul. Complexitatea este
Parcurgerea vecinilor unui nod
Pentru a parcurge nodurile adiacente unui nod dat trebuie să parcurgem toată lista de muchii și să le luăm în considerare doar pe acelea cu una dintre extremități egală cu Din păcate, complexitatea este
Sursă demonstrativă în C++
Mai jos este o sursă demonstrativă pentru reținerea unui graf orientat prin lista sa de muchii. Aceasta prezintă o listă de muchii definită global și implementează funcții pentru operațiile descrise mai sus. Pentru a face sursa să funcționeze cu grafuri neorientate, când comparăm o muchie cu muchia va trebui să o comparăm și pe cu pentru că poate am reținut-o invers în listă. La fel și când parcurgem vecinii unui nod. Va trebui să comparăm nodul dat cu ambele extremități ale muchiei curente.
#include <iostream>using namespace std;
struct Edge { int x, y; Edge(int x = 0, int y = 0) { this->x = x; this->y = y; }};
int m; // numărul de muchiiEdge edg[618]; // lista de muchii
/// Funcția returnează poziția din vector unde se găsește edge,/// sau -1 dacă muchia nu există.int find(Edge edge) { for (int i = 0; i < m; i++) if (edg[i].x == edge.x && edg[i].y == edge.y) return i; return -1;}
void remove(Edge edge) { for (int i = 0; i < m; i++) if (edg[i].x == edge.x && edg[i].y == edge.y) { swap(edg[i], edg[m - 1]); m--; return; }}
void insert(Edge edge) { edg[m++] = edge;}
void neighbors(int node) { for (int i = 0; i < m; i++) if (edg[i].x == node) cout << edg[i].y << ' '; cout << '\n';}
int main() { insert(Edge(5, 1)); insert(Edge(5, 2)); insert(Edge(5, 4));
insert(Edge(5, 3)); remove(Edge(5, 3));
cout << find(Edge(5, 2)) << '\n'; cout << find(Edge(2, 5)) << '\n';
neighbors(5); return 0;}Reprezentarea grafurilor prin matricea de adiacență
Un mod mult mai bun de reprezentare a unui graf se realizează prin folosirea unei așa-numite matrice de adiacență. Aceasta are numărul de linii și numărul de coloane egale cu numărul de noduri ale grafului. Dacă e să o notăm cu (de la adiacență), atunci pe se găsește valoarea true dacă există muchie de la nodul la nodul sau false dacă nu.
Dacă există cost pe muchiile grafului, acesta poate fi stocat în matricea de adiacență, doar că aceasta își va schimba numele în matrice de ponderi. Dacă există muchia pe s-ar reține costul acesteia. Dacă nu, ar avea o valoare pe care nu o poate lua niciun cost (de obicei
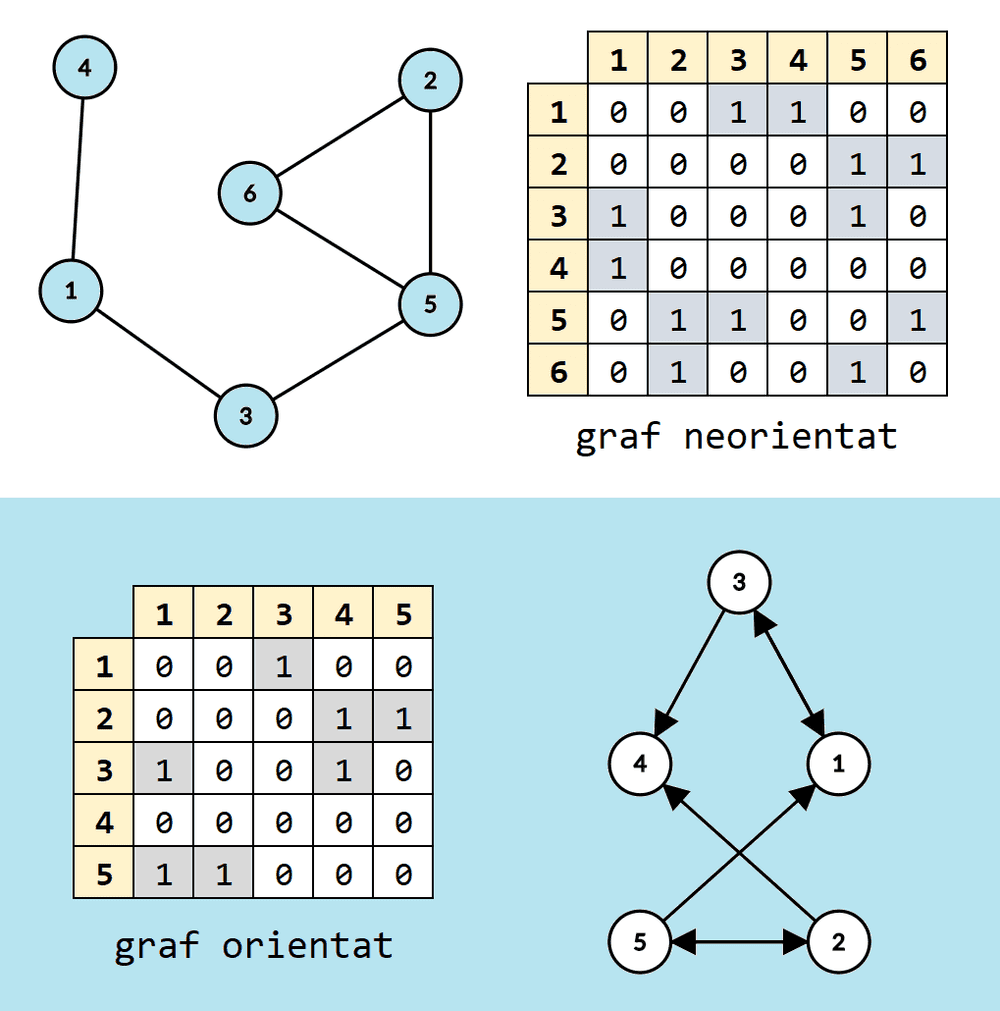
Se poate observa că în cazul unui graf neorientat, matricea de adiacență este simetrică după diagonala principală. Altfel spus, are aceeași valoare cu Este evident, din moment ce și se referă de fapt la aceeași muchie.
Accesarea, inserarea și ștergerea unei muchii
Operațiile de accesare, inserare și ștergere se produc în accesând și modificând elemente din matrice. Însă, la grafurile neorientate trebuie avută un pic de grijă: La inserarea sau ștergerea muchiei trebuie actualizate atât cât și
Parcurgerea vecinilor unui nod
Parcurgerea vecinilor unui nod are complexitatea unde este numărul de noduri din graf: Trebuie parcursă întreaga linie din matrice, și vor fi prelucrate doar elementele cu valoarea true.
Sursă demonstrativă în C++
Iată o sursă demonstrativă pentru reținerea unui graf neorientat prin matricea sa de adiacență. Poate fi adaptată extrem de ușor ca să funcționeze pe grafuri orientate.
#include <iostream>using namespace std;
struct Edge { int x, y; Edge(int x, int y) { this->x = x; this->y = y; }};
int n; // numărul de noduribool ad[NMAX][NMAX]; // matricea de adiacență
bool find(Edge edge) { return ad[edge.x][edge.y];}
void remove(Edge edge) { ad[edge.x][edge.y] = ad[edge.y][edge.x] = false;}
void insert(Edge edge) { ad[edge.x][edge.y] = ad[edge.y][edge.x] = true;}
void neighbors(int node) { for (int j = 1; j <= n; j++) if (ad[node][j]) cout << j << ' '; cout << '\n';}
int main() { n = 5; insert(Edge(1, 2)); insert(Edge(1, 3)); insert(Edge(1, 4)); insert(Edge(4, 5));
insert(Edge(3, 4)); remove(Edge(3, 4));
cout << find(Edge(4, 5)) << '\n'; cout << find(Edge(2, 5)) << '\n';
neighbors(1); neighbors(2); neighbors(3); neighbors(4); neighbors(5); return 0;}Reprezentarea grafurilor prin liste de adiacență
O altă soluție este să reținem câte o listă de adiacență pentru fiecare nod al grafului. Mai exact, lista de adiacență a unui nod va reține nodurile adiacente la acesta. Pentru implementare am putea folosi o matrice, iar fiecare linie să fie lista de adiacență a nodului Însă, n-ar fi o idee prea eficientă ca memorie, pentru că s-ar reține o grămadă de poziții libere la finalul fiecărei linii. Listele ar trebui să fie alocate dinamic, ca să nu ocupe decât atâtea elemente câți vecini are nodul respectiv. Ca să simplific lucrurile, pentru liste am folosit container-ul vector din STL, căci este perfect pentru ce avem nevoie.
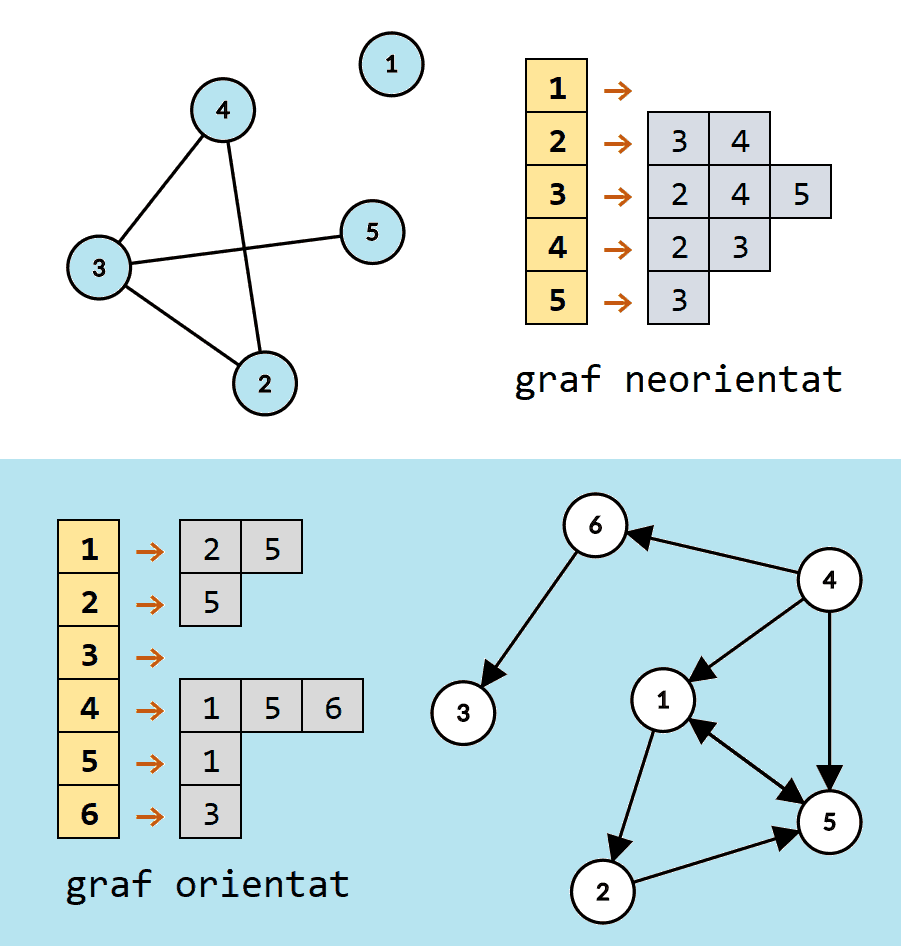
Accesarea unei muchii
Pentru a accesa o muchie trebuie doar să căutăm nodul în lista de adiacență a nodului Complexitatea este Am notat prin numărul de vecini ai nodului voi folosi această notație și în continuare.
Ștergerea unei muchii
Pentru a șterge o muchie căutăm nodul în lista nodului apoi îl ștergem similar modului descris în cazul listei de muchii. Complexitatea este
Inserarea unei muchii
Pentru a insera o muchie adăugăm nodul la sfârșitul listei de adiacență a nodului Complexitatea este
Parcurgerea vecinilor unui nod
Pentru a parcurge nodurile adiacente unui nod dat, trebuie doar să-i parcurgem lista de adiacență. Complexitatea este
Sursă demonstrativă în C++
Mai jos este o sursă demonstrativă pentru reținerea unui graf orientat prin liste de adiacență. Din nou, sursa poate fi modificată ușor ca să funcționeze pentru grafuri neorientate.
#include <vector>#include <iostream>using namespace std;
struct Edge { int x, y; Edge(int x, int y) { this->x = x; this->y = y; }};vector<int> ad[618]; // lista de adiacență
int find(Edge edge) { for (int j = 0; j < int(ad[edge.x].size()); j++) if (ad[edge.x][j] == edge.y) return j; return -1;}
void remove(Edge edge) { for (int j = 0; j < int(ad[edge.x].size()); j++) if (ad[edge.x][j] == edge.y) { swap(ad[edge.x][j], ad[edge.x].back()); ad[edge.x].pop_back(); return; }}
void insert(Edge edge) { ad[edge.x].push_back(edge.y);}
void neighbors(int node) { for (int j = 0; j < int(ad[node].size()); j++) cout << ad[node][j] << ' '; cout << '\n';}
int main() { insert(Edge(5, 1)); insert(Edge(5, 2)); insert(Edge(5, 4));
insert(Edge(5, 3)); remove(Edge(5, 3));
cout << find(Edge(5, 2)) << '\n'; cout << find(Edge(2, 5)) << '\n';
neighbors(5); return 0;}Concluzii
Mai jos aveți un tabel care compară complexitățile celor trei metode de reprezentare a grafurilor. Am evidențiat complexitățile optime pentru fiecare operație.
| Operație | Listă de muchii | Matrice de adiacență | Liste de adiacență |
|---|---|---|---|
| Accesarea unei muchii | |||
| Ștergerea unei muchii | |||
| Inserarea unei muchii | |||
| Parcurgerea vecinilor unui nod |
Reprezentarea unui graf prin lista de muchii este cea mai ineficientă metodă. Este utilă doar atunci când efectiv trebuie să parcurgem muchiile grafului, și cel mult să inserăm niște muchii. Una dintre foarte puținele aplicații practice ale listei de muchii este Algoritmul lui Kruskal.
Matricea de adiacență și listele de adiacență sunt cele mai folosite metode. Prima are cea mai bună complexitate pentru manipularea muchiilor, însă consumă cea mai multă memorie, și nu permite o parcurgere prea eficientă a vecinilor unui nod. Listele de adiacență sunt însă cele mai bune la capitolul din urmă, iar consumul de memorie al acestora depinde doar de numărul de muchii.
Alegerea celei mai potrivite metode de reprezentare a unui graf depinde foarte mult de restricțiile problemei. De obicei însă, matricea de adiacență este mai bună pentru grafurile dense (cu multe muchii), iar listele de adiacență sunt mai bune pentru grafurile rare (cu puține muchii).
Dacă aveți vreo întrebare legată de metodele de reprezentare a grafurilor în C++, nu ezitați să o adresați într-un comentariu, mai jos