Șmenul lui Mars în C++. Aplicații

de Iulian Oleniuc | 23/12/2019 | Algoritmică și structuri de date

Șmenul lui Mars este o metodă eficientă de a efectua un anumit tip de operații asupra unui vector. În engleză, acest șmen se numește Difference Arrays, dar olimpicii români îi spun de cele mai multe ori Șmenul lui Mars, deoarece i l-au atribuit lui Marius Andrei (Mars).

Problema

Problema de bază pe care o rezolvă Șmenul lui Mars sună așa: Se dă un vector $v$ cu $n$ elemente, indexate de la $1$ Se dă de asemenea o listă (mare) de operații codificate sub forma unor triplete $x \text{ } y \text{ } z$ cu semnificația că toate elementele din secvența $[x, y]$ se măresc cu $z$ Să se afișeze elementele vectorului după efectuarea acestor operații.

Exemplu

De pe prima linie a fișierului mars.in se citesc $n$ (lungimea vectorului) și $q$ (numărul de operații). Pe a doua linie se află elementele vectorului $v$ iar pe următoarele $q$ linii sunt scrise operațiile, codificate ca mai sus.

7 3
1 6 1 8 3 1 4
2 4 3
7 7 1
3 7 -2

Pe prima linie a fișierului mars.out se vor afișa elementele finale ale vectorului $v$

1 9 2 9 1 -1 3

Explicație: Elementele vectorului inițial și după fiecare operație sunt:

1  6  1  8  3  1  4
1  9  4 11  3  1  4
1  9  4 11  3  1  5
1  9  2  9  1 -1  3

Soluție

Soluția imediată este să efectuăm fiecare operație parcurgând secvența corespunzătoare și actualizând fiecare element în parte:

for (int it = 0; it < q; it++) {
    cin >> x >> y >> z;
    for (int i = x; i <= y; i++)
        v[i] += z;
}

Cum în cel mai rău caz, fiecare secvență poate fi chiar vectorul în întregime, complexitatea acestei soluții este $O(q \cdot n)$ ceea ce este mult prea mult.

Șmenul lui Mars se bazează pe faptul că nu e nevoie să efectuăm fiecare operație în parte (cel puțin nu în întregime), ci le putem procesa pe toate simultan, la final. În acest sens, luăm un vector suplimentar $\mathrm{mars}$ inițializat cu zero peste tot. Pentru fiecare operație $x \text{ } y \text{ } z$ adunăm valoarea $z$ la elementul de pe poziția $x$ și o scădem din elementul de pe poziția $y + 1$

for (int i = 0; i < q; i++) {
    cin >> x >> y >> z;
    mars[x] += z;
    mars[y + 1] -= z;
}

La final, suma primelor $i$ elemente din $\mathrm{mars}$ va reprezenta de fapt cu cât se modifică valoarea inițială a lui $v[i]$ în urma operațiilor date. Deci, ca să reconstituim vectorul $v$ trebuie să construim șirul sumelor parțiale ale vectorului $\mathrm{mars}$

for (int i = 1; i <= n; i++) {
    mars[i] += mars[i - 1];
    v[i] += mars[i];
}

Motivul pentru care asta funcționează este foarte simplu: E clar că $\mathrm{mars}[i]$ a primit update de la toate operațiile pe secvențe din care $i$ face parte, deoarece $z$ urile respective au fost adunate la elemente din stânga lui $i$ Totodată, $\mathrm{mars}[i]$ nu a primit update de la operațiile pe secvențe ce se termină înaintea lui $i$ pentru că ele au contribuit la suma parțială și cu $+z$ și cu $-z$ care se anulează. Evident, operațiile asupra secvențelor ce încep după $i$ n-au cum să afecteze valoarea finală a lui $\mathrm{mars}[i]$ Așadar, șmenul rezolvă problema dată corect. Iată sursa completă:

Șmenul lui Mars
#include <bits/stdc++.h>
using namespace std;

ifstream fin("mars.in");
ofstream fout("mars.out");

int main() {
    int n, q; fin >> n >> q;
    vector<int> v(n + 1);
    for (int i = 1; i <= n; i++)
        fin >> v[i];

    vector<int> mars(n + 2);
    for (int i = 0; i < q; i++) {
        int x, y, z; fin >> x >> y >> z;
        mars[x] += z;
        mars[y + 1] -= z;
    }

    for (int i = 1; i <= n; i++) {
        mars[i] += mars[i - 1];
        v[i] += mars[i];
        fout << v[i] << ' ';
    }
    fout << '\n';
    return 0;
}

Complexitatea acestei soluții este $O(1)$ pentru fiecare operație și $O(n)$ pentru reconstituirea vectorului, deci $O(q + n)$ în total. Șmenul lui Mars este eficient atunci când avem nevoie la final (sau nu numai) de toate elementele modificate. (Ca să-l reconstituim pe $v$ de mai multe ori, adică printre update-uri, nu trebuie decât ca după fiecare reconstituire să umplem din nou vectorul $\mathrm{mars}$ cu $0$

Șmenul lui Mars poate fi adaptat și pentru situația în care al doilea tip de operație cere valoarea unui anumit element, nu valorile tuturor elementelor. Pentru a determina valoarea curentă a lui $v[i]$ vom calcula sumele parțiale doar până în poziția $i$ și vom reinițializa cu $0$ doar primele i poziții din $\mathrm{mars}$ (Se vor reconstitui automat primele $i$ elemente din $v$ nu doar al $i$ lea.) Totuși, în acest context, Șmenul lui Mars nu mai este eficient decât dacă avem de efectuat foarte puține interogări. În caz contrar, soluția optimă necesită arbori de intervale cu lazy update :wink:

Extinderea șmenului în două dimensiuni

Putem aplica Șmenul lui Mars și într-o matrice. Dacă avem de făcut update pe submatricea de coordonate $(x_1, y_1)$ și $(x_2, y_2)$ procedăm astfel:

mars[x1][y1] += val;
mars[x1][y2 + 1] -= val;
mars[x2 + 1][y1] -= val;
mars[x2 + 1][y2 + 1] += val;

Iar pentru reconstituirea matricei vom folosi tot sume parțiale, dar în varianta 2D:

for (int i = 1; i <= n; i++)
    for (int j = 1; j <= n; j++)
        mars[i][j] += mars[i - 1][j] + mars[i][j - 1] - mars[i - 1][j - 1];

Aplicații

De cele mai multe ori, Șmenul lui Mars reprezintă doar o mică parte din rezolvarea unei probleme, și se aplică exact pentru task-ul general prezentat în acest articol. Iată totuși două probleme mai interesante ce folosesc șmenul:

Fibo4 (InfoOltenia 2018, Clasa a 10-a)

Enunțul problemei Fibo4 se poate găsi pe InfoArena. Se dă un vector $v$ cu $n$ elemente, inițial toate nule. Asupra lui se aplică $q$ update-uri de forma $x \text{ } y \text{ } k$ cu semnificația că la fiecare element $v[i]$ cu $x \le i \le y$ se adaugă valoarea $fib(k + i - x)$ unde $fib(n)$ reprezintă al $n$ lea termen din Șirul lui Fibonacci. Să se afișeze configurația finală a vectorului, modulo $666013$

Soluția se bazează pe Șmenul lui Mars ușor modificat. Update-urile se vor efectua așa:

mars[x] += fib(k);
mars[x + 1] += fib(k - 1);
mars[y + 1] -= fib(k + y - x + 1);
mars[y + 2] -= fib(k + y - x);

Reconstituirea trebuie modificată și ea un pic:

for (int i = 2; i <= n; i++)
    mars[i] += mars[i - 1] + mars[i - 2];

Să analizăm ce se întâmplă când construim sumele parțiale dacă facem un singur update:

mars[x    ] <- fib(k) + 0 + 0 = fib(k)
mars[x + 1] <- fib(k - 1) + fib(k) + 0 = fib(k + 1)
mars[x + 2] <- 0 + fib(k + 1) + fib(k) = fib(k + 2)
...
mars[y    ] <- 0 + fib(k + y - x - 1) + fib(k + y - x - 2) = fib(k + y - x)
mars[y + 1] <- -fib(k + y - x + 1) + fib(k + y - x) + fib(k + y - x - 1) = 0
mars[y + 2] <- -fib(k + y - x) + 0 + fib(k + y - x) = 0

Din nou, se vede clar că șmenul și-a făcut treaba corect.

Pentru fiecare update avem nevoie de patru termeni Fibonacci modulo $666013$ Putem să-i calculăm pe fiecare în parte folosind exponențiere logaritmică pe matrice, însă am obține doar 40 de puncte, pentru că trebuie să calculăm $O(q)$ termeni, ceea ce e prea mult dacă pui și factorul $\log_2 10^{18}$ Soluția optimă se folosește de faptul că resturile termenilor Fibonacci sunt periodice modulo un anumit număr (vezi Perioada Pisano). Perioada corespunzătoare lui $666013$ este $1332028$ un număr rezonabil de mic. Vom precalcula așadar resturile primilor $1332028$ termeni Fibonacci în timp liniar, iar când vom avea nevoie de $fib(n) \modd 666013$ vom folosi restul de pe poziția $n \modd 1332028$

În această problemă am învățat că Șmenul lui Mars se poate adapta și la update-uri mai complexe, și am aflat de existența Perioadei Pisano, care este și ea utilă. Iată sursa de 100 de puncte:

Problema Fibo4
#include <bits/stdc++.h>
using namespace std;

ifstream fin("fibo4.in");
ofstream fout("fibo4.out");

const int PI = 1332028;
const int MOD = 666013;

int main() {
    vector<int> fib(PI);
    fib[1] = 1;
    for (int i = 2; i < PI; i++)
        fib[i] = (fib[i - 1] + fib[i - 2]) % MOD;

    int n, q; fin >> n >> q;
    vector<int> mars(n + 3);
    for (int i = 0; i < q; i++) {
        int x, y; int64_t k; fin >> x >> y >> k;
        mars[x] = (mars[x] + fib[k % PI]) % MOD;
        mars[x + 1] = (mars[x + 1] + fib[(k - 1) % PI]) % MOD;
        mars[y + 1] = (mars[y + 1] - fib[(k + y - x + 1) % PI] + MOD) % MOD;
        mars[y + 2] = (mars[y + 2] - fib[(k + y - x) % PI] + MOD) % MOD;
    }

    fout << mars[1] << ' ';
    for (int i = 2; i <= n; i++) {
        mars[i] = (mars[i] + mars[i - 1] + mars[i - 2]) % MOD;
        fout << mars[i] << ' ';
    }
    fout << '\n';
    return 0;
}

Fisherman (SEERC 2018)

Enunțul problemei Fisherman se găsește pe CodeForces (la Contest materials > Statements). Avem un sistem cartezian, în care $n$ pești și $m$ pescari sunt reprezentați prin puncte de coordonate date. Pescarii se află pe axa $OX$ Fiecare pescar are undița de lungime $l$ putând pescui doar pești aflați la distanță Manhattan cel mult $l$ de el. Aflați câți pești poate pescui fiecare pescar.

Un pește poate fi prins doar de pescarii aflați la distanță Manhattan cel mult $l$ de el. Această zonă formează un romb ca în imaginea de mai jos. Pescarii ce pot prinde acest pește se află pe segmentul determinat de intersecția dintre romb și axa $OX$

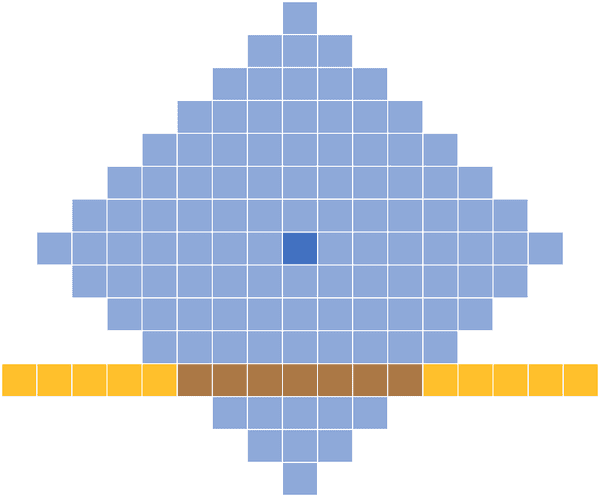
Capetele segmentului se pot calcula foarte ușor: $x - l + y$ la stânga și $x + l - y$ la dreapta. Luăm un vector $\mathrm{mars}$ inițializat cu zero, ce reprezintă axa $OX$ Problema se reduce la a efectua următoarea operație pentru fiecare pește: Să se adauge $1$ la fiecare element din intervalul $[x - l + y, x + l - y]$ La final, în $\mathrm{mars}[i]$ vom avea soluția pentru pescarul cu abscisa $i$ Putem face update-urile astea cu Șmenul lui Mars, doar că avem o problemă: Vectorul $\mathrm{mars}$ ar trebui să aibă un miliard de elemente, din cauza valorii maxime a coordonatelor.

Ideea e că de fapt nu avem nevoie decât de $m$ elemente, corespunzătoare celor $m$ pescari. Pentru fiecare pește vom crea două evenimente: $(x - l + y, +1)$ și $(x + l - y + 1, -1)$ cu semnificația că de la abscisa $x - l + y$ se adaugă $1$ iar de la $x + l - y + 1$ se scade $1$ Punem toate evenimentele într-un vector pe care îl sortăm. Sortăm și vectorul cu pescarii, iar apoi practic îl interclasăm cu vectorul de evenimente. Când am ajuns la un pescar cu abscisa mai mare sau egală cu abscisa evenimentului curent, adunăm sau scădem $1$ din $\mathrm{mars}[j]$ în funcție de tipul evenimentului.

În această problemă am învățat ce trebuie făcut când lucrăm cu update-uri pe vectori prea mari, câte ceva despre distanța Manhattan și poate un mod mai clar de a interclasa doi vectori (util când răspundem la query-uri offline). Iată sursa de 100 de puncte care ia Accepted:

Problema Fisherman
#include <bits/stdc++.h>
using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m, l; cin >> n >> m >> l;
    vector<pair<int, int>> ev;
    for (int i = 0; i < n; i++) {
        int x, y; cin >> x >> y;
        if (y <= l) {
            ev.emplace_back(x - l + y, +1);
            ev.emplace_back(x + l - y + 1, -1);
        }
    }

    vector<pair<int, int>> pt(m);
    for (int i = 0; i < m; i++) {
        cin >> pt[i].first;
        pt[i].second = i;
    }

    sort(ev.begin(), ev.end());
    sort(pt.begin(), pt.end());

    vector<int> mars(m);
    for (int i = 0, j = 0; i < int(ev.size()); i++) {
        while (j < m && pt[j].first < ev[i].first)
            j++;
        if (j == m)
            break;
        mars[j] += ev[i].second;
    }

    vector<int> sol(m);
    for (int i = 0; i < m; i++) {
        if (i)
            mars[i] += mars[i - 1];
        sol[pt[i].second] = mars[i];
    }

    for (int i = 0; i < m; i++)
        cout << sol[i] << '\n';
    return 0;
}

Dacă aveți vreo întrebare despre Șmenul lui Mars, sau dacă știți alte probleme interesante ce folosesc această tehnică, nu ezitați să lăsați un comentariu mai jos :smile: