Sortarea prin inserție (Insertion Sort) în C++

Sortarea prin inserție (Insertion Sort) este o metodă de sortare a vectorilor în complexitate $O(n^2)$ oarecum asemănătoare cu sortarea prin selecție. Vom considera că dorim să sortăm crescător vectorul $v$ de lungime $n$ indexat de la $1$

Algoritm

Sortarea prin inserție presupune că, la fiecare pas $i \gt 1$ primele $i - 1$ elemente din vector sunt deja sortate. Urmează să extindem această secvență de elemente sortate folosind elementul curent, $v[i]$ Pentru a vedea pe ce poziție trebuie să-l inserăm pe $v[i]$ pur și simplu parcurgem elementele de la stânga lui $i$ căutând unul mai mic sau egal cu $v[i]$ Dacă notăm poziția la care am găsit acest element cu $j$ (în caz că nu există un astfel de element, considerăm $j = 0$ atunci $v[i]$ va fi inserat pe poziția $j + 1$ Putem fie să apropiem treptat elementul $v[i]$ de poziția căutată, interschimbând la fiecare pas elementele $v[j]$ și $v[j - 1]$ ca mai jos…

for (int i = 2; i <= n; i++)
    for (int j = i; j > 1 && v[j - 1] > v[j]; j--) {
        int aux = v[j];
        v[j] = v[j - 1];
        v[j - 1] = aux;
    }

Fie să mutăm elementele mai mari decât $v[i]$ cu o poziție la dreapta, în timp ce le parcurgem, urmând ca la final să-l copiem pe $v[i]$ pe poziția $j$ Pentru asta vom avea nevoie de o variabilă auxiliară $aux$ unde să-l copiem la început pe $v[i]$ Varianta aceasta este mai eficientă, efectuând de $3$ ori mai puține atribuiri.

for (int i = 2; i <= n; i++) {
    int j, aux = v[i];
    for (j = i; j > 1 && v[j - 1] > aux; j--)
        v[j] = v[j - 1];
    v[j] = aux;
}

Exemplu

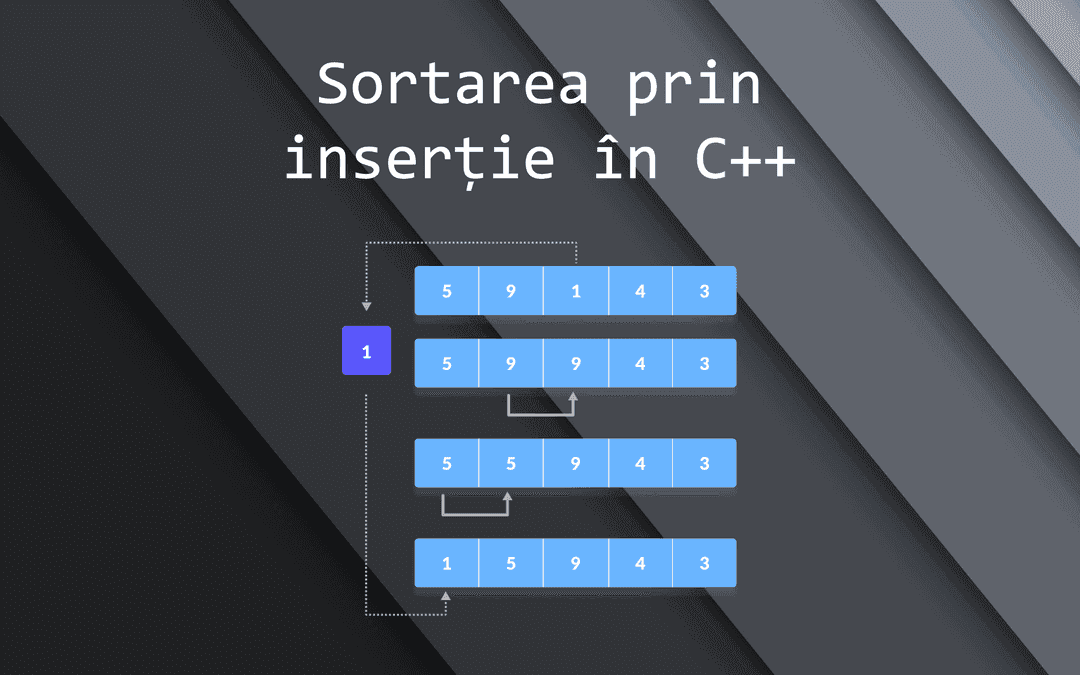
Iată mai jos o vizualizare a algoritmului. Am colorat cu roșu elementul $v[i]$ cu galben $v[j]$ cu verde elementele sortate și cu alb pe celelalte.

Complexitate

Primul for efectuează $O(n)$ iterații, iar al doilea, în cel mai rău caz, tot $O(n)$ Prin urmare, complexitatea în timp a sortării prin inserție este $O(n^2)$ Cel mai rău caz este atins atunci când vectorul dat este sortat invers (descrescător). Cel mai bun caz, în care algoritmul rulează în $O(n)$ este cel în care vectorul e deja sortat.

Având în vedere că elementele de la stânga lui $i$ sunt sortate, putem căuta binar poziția $j$ la care trebuie să-l inserăm pe $v[i]$ Astfel, am reduce numărul de comparații de la fiecare pas de la $O(n)$ la $O(\log n)$ Totuși, optimizarea asta nu schimbă complexitatea finală, pentru că oricum mutarea elementelor la dreapta consumă $O(n)$ operații.

Dacă aveți vreo întrebare legată de sortarea prin inserție în C++, nu ezitați să o lăsați mai jos, într-un comentariu