Sortarea prin numărare (Counting Sort) în C++

Sortarea prin numărare (Counting Sort) este o metodă de sortare a vectorilor ce se bazează pe utilizarea unui vector de frecvență. Acest algoritm de sortare poate fi extrem de eficient în anumite situații, în funcție de intervalul de valori al elementelor vectorului. Vom considera că vrem să sortăm un vector $v$ de lungime $n$ indexat de la $1$ și cu elementele cuprinse între $0$ și $\mathrm{MAX} - 1$

Algoritm

Se parcurge vectorul $v$ și se rețin frecvențele elementelor sale în vectorul de frecvență $\mathrm{frq}$ Apoi, se parcurge vectorul $\mathrm{frq}$ de la $0$ la $\mathrm{MAX} - 1$ dacă vrem să realizăm o sortare crescătoare, sau de la $\mathrm{MAX} - 1$ la $0$ în caz contrar. Considerăm $k$ noua lungime a vectorului, și o inițializăm cu $0$ Pentru fiecare element $\mathrm{frq}[i]$ adăugăm valoarea $i$ la finalul vectorului (pe poziția $k$ ce mai întâi este incrementată) de $\mathrm{frq}[i]$ ori, pentru că de atâtea ori apare aceasta în $v$ Ordinea în care este parcurs vectorul de frecvență ne garantează că elementele vor fi reintroduse în vector gata sortate.

Exemplu

Am notat vectorul inițial cu $v$ vectorul sortat cu $w$ iar vectorul de frecvență cu $\mathrm{frq}$

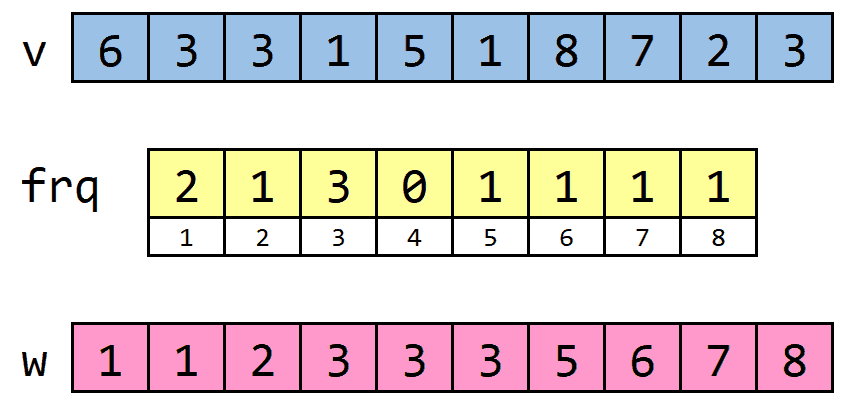
Implementare în C++

Mai jos este implementarea algoritmului în C++. Nimic special… L-am parcurs pe $v$ de la $1$ la $n$ și am actualizat frecvența (numărul de apariții) ale elementului curent $\htmlClass{katexified}{(} v[i]$ prin frq[v[i]]++. Apoi, l-am parcurs pe $\mathrm{frq}$ de la $0$ la $\mathrm{MAX} - 1$ (pentru că ăsta e intervalul de valori al elementelor lui $v$ Pentru fiecare element $\mathrm{frq}[i]$ cât timp e nenul, îl decrementez, incrementez noul capăt al lui $v$ $\htmlClass{katexified}{(} k$ și îl copiez acolo pe $i$

for (int i = 1; i <= n; i++)
    frq[v[i]]++;
int k = 0;
for (int i = 0; i < MAX; i++)
    while (frq[i]--)
        v[++k] = i;

Se observă că sortarea prin numărare nu este un algoritm de sortare prin comparare, deoarece nu se efectuează nicio comparație între elementele vectorului. Soluția poate fi adaptată și pentru cazul în care intervalul de valori al lui $v$ conține și numere negative, așa cum am descris în articolul Vectori caracteristici. Vectori de frecvență.

În plus, dacă nu avem nevoie de forma inițială a vectorului (cea nesortată), putem calcula frecvențele încă din timpul citirii vectorului. De asemenea, dacă nu trebuie decât să afișăm vectorul sortat, putem afișa elementele direct în while, fără să mai reconstruim vectorul. Iată mai jos o sursă completă care citește un șir de numere, și le afișează în ordine crescătoare, folosind sortarea prin numărare.

#include <bits/stdc++.h>
using namespace std;
const int MAX = 618;

int n;
int frq[MAX];

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        int x; cin >> x;
        frq[x]++;
    }
    for (int i = 0; i < MAX; i++)
        while (frq[i]--)
            cout << i << ' ';
    cout << '\n';
    return 0;
}

Complexitate

Sortarea prin numărare face $2 \cdot n + \mathrm{MAX}$ pași. Un $n$ de la parcurgerea lui $v$ un $\mathrm{MAX}$ de la parcurgerea lui $\mathrm{frq}$ și încă un $n$ de la reintroducerea elementelor în $v$ Asta înseamnă o complexitate liniară, de ordinul $O(n + \mathrm{MAX})$ Complexitatea spațiului auxiliar este $O(\mathrm{MAX})$ pentru că este necesar un vector de frecvență de lungime $\mathrm{MAX}$

Totuși, deși complexitatea algoritmului este liniară, acesta nu este fezabil în orice condiții. El este eficient doar când lungimea intervalului de valori ale elementelor din vector este suficient de mică în raport cu lungimea vectorului. Mai exact, sortarea prin numărare bate un algoritm de complexitate $O(n \log n)$ cum ar fi QuickSort, atunci când $\mathrm{MAX} \lt n \log_2 n$ Similar, sortarea prin numărare e mai bună decât un algoritm în $O(n^2)$ ca sortarea prin selecție, când $\mathrm{MAX} \lt n^2$

Dacă aveți vreo întrebare despre metoda sortării prin numărare, nu ezitați să o adresați mai jos într-un comentariu