Sume parțiale în C++. Probleme cu sume parțiale

Sumele parțiale reprezintă o noțiune pe cât de simplă, pe atât de utilă. Ele sunt folosite într-o grămadă de probleme de informatică, așa că în acest articol voi prezenta cele mai importante tehnici ce folosesc conceptul de sume parțiale.

Definiție

Fie $v$ un vector de $n$ numere indexate de la $1$ Vectorului $v$ îi vom asocia un șir $\mathrm{ps}$ cu proprietatea:

Acest șir se numește șirul sumelor parțiale ale lui $v$ De aici și notația (partial sums). Deci, $\mathrm{ps}[i]$ reprezintă suma primelor $i$ elemente ale vectorului dat, adică a $i$a sumă parțială a lui $v$ Prin convenție, $\mathrm{ps}[0] = 0$ pentru că $0$ este elementul neutru la adunare. Șirul $\mathrm{ps}$ poate fi calculat foarte ușor în timp liniar bazându-ne pe următoarea relație de recurență:

Această recurență face construcția șirului de sume parțiale să poată fi considerată o problemă de programare dinamică. Desigur, una foarte simplă.

vector<int> ps(n + 1);
for (int i = 1; i <= n; i++)
    ps[i] = ps[i - 1] + v[i];

Aplicații

Putem trece deja la aplicații! Am încercat să aleg 6 probleme clasice prin care să ilustrez cât mai multe tehnici ce folosesc conceptul de sume parțiale.

Problema 1.

Se dă un vector $v$ cu $n$ numere întregi, precum și $q$ întrebări de forma $x \text{ } y$ cu semnificația: Care este suma elementelor din $v$ cuprinse între indicii $x$ și $y$ Să se răspundă eficient la cele $q$ întrebări.

Asta e probabil cea mai cunoscută problemă de sume parțiale, și cred că de aici a și apărut nevoia de acest concept. Evident, o soluție ar fi să parcurgem secvența corespunzătoare fiecărei întrebare, însă am avea o complexitate de ordinul $O(q \cdot n)$ Soluția liniară se obține observând următorul lucru: Suma elementelor din secvența determinată de indicii $x$ și $y$ este egală cu $\mathrm{ps}[y] - \mathrm{ps}[x - 1]$ Deci, după ce citim vectorul $v$ sau chiar în timpul citirii, construim șirul $\mathrm{ps}$ iar apoi răspundem la fiecare întrebare în $O(1)$ folosind această formulă. Astfel, obținem complexitatea $O(n + q)$

int n; cin >> n;
vector<int> ps(n + 1);
for (int i = 1; i <= n; i++) {
    int x; cin >> x;
    ps[i] = ps[i - 1] + x;
}

int q; cin >> q;
for (int i = 0; i < q; i++) {
    int x, y; cin >> x >> y;
    cout << ps[y] - ps[x - 1] << '\n';
}

Problema 2.

Se dă un număr natural $k$ și un vector $v$ cu $n$ numere naturale. Atât $k$ cât și suma elementelor lui $v$ sunt mai mici sau egale cu $10^6$ Să se determine o secvență a lui $v$ cu proprietatea că suma elementelor ei este egală cu $k$

Pentru a obține o soluție liniară, ne bazăm pe faptul că dacă o secvență $[x + 1, y]$ are suma elementelor $k$ atunci $\mathrm{ps}[y] - \mathrm{ps}[x] = k$ Deci, dacă există vreo astfel de secvență care să aibă capătul din dreapta în $y$ atunci trebuie să existe și un indice $x \lt y$ pentru care $\mathrm{ps}[x] = \mathrm{ps}[y] - k$ Putem găsi rapid un astfel de indice în timpul calculării sumelor parțiale folosind un vector suplimentar $\mathrm{pos}$ În $\mathrm{pos}[i]$ vom reține un indice $x \ge 0$ găsit până la pasul curent, astfel încât $\mathrm{ps}[x] = i$ sau $-1$ dacă încă n-am găsit un astfel de indice.

Dacă la pasul $i$ am obținut o sumă parțială $ps$ pentru care $\mathrm{pos}[ps - k] \neq -1$ afișăm indicii $\mathrm{pos}[ps] + 1$ și $i$ după care ne oprim. Trebuie să avem grijă ca nu cumva să uităm de $\mathrm{ps}[0]$ În acest sens, la început trebuie să inițializăm $\mathrm{pos}[0]$ cu valoarea $0$

vector<int> pos(1e6 + 1, -1);
int ps = 0;
pos[0] = 0;
int n; cin >> n;
for (int i = 1; i <= n; i++) {
    int x; cin >> x;
    ps += x;
    if (ps - k >= 0 && pos[ps - k] != -1) {
        cout << pos[ps - k] + 1 << ' ' << i << '\n';
        return 0;
    }
    pos[ps] = i;
}

Problema 3.

Se dă un număr $k \gt 0$ și un vector $v$ cu $n$ elemente. Atât $k$ cât și elementele lui $v$ sunt numere naturale, până în $10^9$ Să se determine o secvență a lui $v$ cu proprietatea că suma elementelor ei este egală cu $k$

Aproape aceeași problemă cu cea precedentă, doar că acum numerele din $v$ pot lua valori egale cu un miliard, motiv pentru care sumele parțiale pot ieși din tipul int, așa că sigur nu putem folosi ideea cu vectorul $\mathrm{pos}$ Bine, dacă e să fim try-hard, putem înlocui vectorul din urmă cu un tabel de hashing (care cam trebuie făcut de mână), dar hai să vedem totuși o altă idee, suficient de rapidă.

Elementele lui $v$ sunt în continuare numere naturale, ceea ce ne garantează monotonia șirului $\mathrm{ps}$ Diferența dintre doi termeni consecutivi ai lui $\mathrm{ps}$ este nenegativă, de unde șirul este crescător. Ei bine, monotonia lui $\mathrm{ps}$ ne duce cu gândul la faptul că putem folosi căutare binară. Așadar, pentru fiecare indice $j \ge 1$ căutăm binar cel mai din stânga indice $i \lt j$ cu proprietatea că $\mathrm{ps}[j] - \mathrm{ps}[i] \le k$ Dacă obținem un indice pentru care diferența dintre cele două sume parțiale este egală cu $k$ înseamnă că am găsit secvența căutată.

vector<int> ps(n + 1);
for (int i = 1; i <= n; i++)
    ps[i] = ps[i - 1] + v[i];
for (int j = 1; j <= n; j++) {
    int lo = -1, hi = j;
    while (hi - lo > 1) {
        int md = (lo + hi) / 2;
        if (ps[j] - ps[md] > k)
            lo = md;
        else
            hi = md;
    }
    if (ps[j] - ps[hi] == k) {
        cout << hi + 1 << ' ' << j << '\n';
        return 0;
    }
}

Dacă ne gândim puțin, putem folosi fără probleme funcția lower_bound din STL, căutarea binară fiind până la urmă pe un vector, nu pe o funcție:

vector<int> ps(n + 1);
for (int i = 1; i <= n; i++)
    ps[i] = ps[i - 1] + v[i];
for (int j = 1; j <= n; j++) {
    int i = lower_bound(ps.begin(), ps.begin() + j, ps[j] - k) - ps.begin();
    if (ps[j] - ps[i] == k) {
        cout << i + 1 << ' ' << j << '\n';
        return 0;
    }
}

O problemă în care am folosit ideea de căutare binară pe șirul sumelor parțiale este br.

Problema 4.

Se dă un vector $v$ cu $n$ elemente numere naturale. Să se determine o secvență a lui $v$ astfel încât suma elementelor ei să fie divizibilă cu $n$

Vom construi din nou șirul sumelor parțiale ale lui $v$ dar de această dată le vom calcula modulo $n$ Deci, $\mathrm{ps}[i] = (v[1] + v[2] + \cdots + v[i]) \modd n$ Astfel, $\mathrm{ps}[j] - \mathrm{ps}[i]$ ne va da restul împărțirii la $n$ a sumei elementelor secvenței $[i + 1, j]$ Noi vrem ca acest rest să fie $0$ deci $\mathrm{ps}[i]$ și $\mathrm{ps}[j]$ trebuie să fie egale (modulo $n$

Așadar, trebuie doar să căutăm doi indici $i$ și $j$ pentru care $\mathrm{ps}[i] = \mathrm{ps}[j]$ Întrebarea este: Vor exista întotdeauna doi astfel de indici? Da, conform principiului lui Dirichlet. Acesta ne spune că dacă alegem $n + 1$ elemente dintr-o mulțime cu $n$ elemente, atunci sigur vor exista măcar două elemente egale. În cazul nostru, alegem $n + 1$ elemente pentru că avem $n + 1$ sume parțiale, iar mulțimea din care alegem elementele este mulțimea resturilor modulo $n$ care clar are $n$ elemente: $\{0, 1, \ldots, n - 1\}$

Pentru a găsi ușor un indice $i \lt j$ astfel încât $\mathrm{ps}[i] = \mathrm{ps}[j]$ vom folosi din nou ideea cu vectorul $\mathrm{pos}$ de la problema 2.

vector<int> pos(n + 1, -1);
int ps = 0;
pos[0] = 0;
int n; cin >> n;
for (int i = 1; i <= n; i++) {
    int x; cin >> x;
    ps = (ps + x) % n;
    if (pos[ps] != -1) {
        cout << pos[ps] + 1 << ' ' << i << '\n';
        return 0;
    }
    pos[ps] = i;
}

Problema 5.

Se dă o matrice $a$ cu $m$ linii și $n$ coloane. Să se determine suma maximă a elementelor unei submatrice a lui $a$ cu $x$ linii și $y$ coloane.

Vom nota cu $s(i_1, j_1, i_2, j_2)$ suma elementelor submatricei cu colțurile stânga-sus și dreapta-jos în $(i_1, j_1)$ și respectiv $(i_2, j_2)$ În total avem $(m - x + 1)(n - y + 1)$ submatrice cu $x$ linii și $y$ coloane – câte una pentru fiecare celulă $(i, j)$ cu $i \ge x$ și $j \ge y$ Dacă ar fi să parcurgem fiecare astfel de submatrice ca să-i calculăm suma, am obține complexitatea $O(m^2 n^2)$ Însă, putem afla suma elementelor unei submatrice în $O(1)$ precalculând niște sume parțiale 2D: În $\mathrm{ps}[i][j]$ reținem $s(1, 1, i, j)$ Relația de recurență este:

Practic, prin $\mathrm{ps}[i - 1][j]$ adunăm $s(1, 1, i - 1, j - 1) + s(1, j, i - 1, j)$ iar prin $\mathrm{ps}[i][j - 1]$ adunăm $s(1, 1, i - 1, j - 1) + s(i, 1, i, j - 1)$ Dacă îl mai adunăm și pe $a[i][j]$ e aproape gata, doar că pe $s(1, 1, i - 1, j - 1)$ l-am adunat de două ori, motiv pentru care trebuie să-l scădem pe $\mathrm{ps}[i - 1][j - 1]$

Acum că avem calculate aceste sume parțiale, putem determina $s(i_1, j_1, i_2, j_2)$ folosind următoarea formulă:

Justificarea e similară cu cea de mai devreme: Scădem două porțiuni de care n-avem nevoie, dar pentru că l-am scăzut de două ori pe $s(1, 1, i_1 - 1, j_1 - 1)$ îl adunăm înapoi. Iată și un desen, sugestiv sper eu:

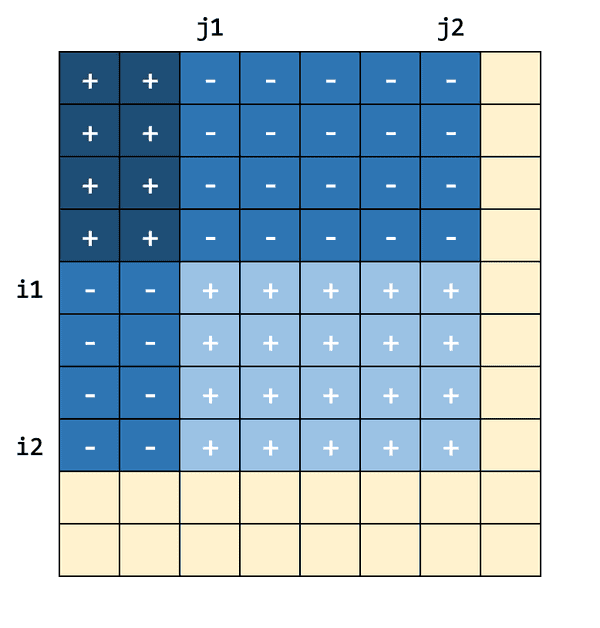
Astfel, am obținut un algoritm optim, de complexitate $O(mn)$ Iată și codul:

vector ps(m + 1, vector<int>(n + 1));
for (int i = 1; i <= m; i++)
    for (int j = 1; j <= n; j++)
        ps[i][j] = ps[i - 1][j] + ps[i][j - 1] - ps[i - 1][j - 1] + a[i][j];

int ans = 0;
for (int i1 = 1, i2 = x; i2 <= m; i1++, i2++)
    for (int j1 = 1, j2 = y; j2 <= n; j1++, j2++)
        ans = max(ans, ps[i2][j2] - ps[i1 - 1][j2] - ps[i2][j1 - 1] + ps[i1 - 1][j1 - 1]);
cout << ans << '\n';

Problema 6.

Se dă un vector $v$ cu $n$ elemente din mulțimea $\{0, 1\}$ Să se determine numărul de secvențe ale lui $v$ ce conțin de două ori mai mulți de $1$ decât de $0$

Asta e o problemă pe care tocmai am propus-o pe PbInfo; o puteți trimite aici. Ideea am întâlnit-o într-o problemă de ONI pe care am rezolvat-o mai demult, doar că acolo apărea într-un context mult mai complex.

Ca de obicei, construim șirul sumelor parțiale ale lui $v$ Observația de bază este că dacă o secvență $[i + 1, j]$ îndeplinește condiția din enunț, atunci $3(\mathrm{ps}[j] - \mathrm{ps}[i]) = 2(i - j)$ Adică numărul de $1$ din secvența $[x, y]$ este $2/3$ înmulțit cu lungimea secvenței. Dacă trecem termenii care depind de $i$ în stânga, iar pe cei care depind de $j$ în dreapta, obținem $2i - 3\mathrm{ps}[i] = 2j - 3\mathrm{ps}[j]$

Asta înseamnă că numărul secvențelor căutate care se termină în $j$ este egal cu numărul indicilor $i \lt j$ ce verifică relația de mai sus. Prin urmare, soluția este ca în timp ce calculăm sumele parțiale ale lui $v$ să reținem într-un vector de frecvență $\mathrm{frq}$ de câte ori am obținut suma $2j - 3\mathrm{ps}[j]$ până la pasul curent. Cum pentru fiecare $j$ se efectuează o interogare și o actualizare în vectorul de frecvență, ambele în timp constant, complexitatea finală devine $O(n)$

În timpul implementării trebuie să fim atenți la trei detalii:

• Răspunsul este de ordinul $O(n^2)$ (la fel ca numărul de secvențe ale lui $v$ așa că trebuie reținut într-o variabilă de tipul long long int.
• Înainte să analizăm fiecare $j$ posibil, trebuie să actualizăm frecvența lui $\mathrm{ps}[0]$
• Valorile $2i - 3\mathrm{ps}[i]$ pot fi și negative, așa că vectorul de frecvență trebuie decalat cu $-k$ poziții la dreapta, unde $k$ este valoarea minimă ce poate fi obținută. Aceasta este $-n$ și se atinge atunci când $i = n$ și $\mathrm{ps}[n] = n$ Valoarea maximă este $2n$ și se atinge când $i = n$ și $\mathrm{ps}[n] = 0$

int n; fin >> n;
vector<int> frq(3 * n + 1);
frq[n] = 1;
int ps = 0;
int64_t sol = 0;
for (int i = 1; i <= n; i++) {
    bool x; fin >> x; ps += x;
    sol += frq[2 * i - 3 * ps + n]++;
}
fout << sol << '\n';

Alte operații?

Cred că v-am convins că sumele parțiale sunt foarte utile, dar le putem folosi oare și pentru alte operații? De exemplu, putem ca în loc de sume parțiale să facem minime parțiale? Răspunsul este că depinde de tipul operației.

Dacă operația $\circ$ este reversibilă, putem calcula suma elementelor oricărei secvențe a vectorului nostru bazându-ne pe sume parțiale. (Aici prin suma pe o secvență $[i, j]$ mă refer la $v[i] \circ v[i + 1] \circ \cdots \circ v[j]$ Să presupunem că $a \circ b = c$ Operația $\circ$ se numește reversibilă dacă putem atât să calculăm $a \circ b$ cât și să facem inversa acestei operații, și anume dacă știm rezultatul $\htmlClass{katexified}{(} c$ și unul dintre termeni $\htmlClass{katexified}{(} b$ să îl aflăm pe celălalt termen $\htmlClass{katexified}{(} a$ Două operații comune care au proprietatea de a fi reversibile sunt adunarea $\htmlClass{katexified}{(} +$ și disjuncția exclusivă $\htmlClass{katexified}{(} \mathrm{xor}$

Printre operațiile care nu sunt reversibile se numără $\min$ $\max$ și $\mathrm{cmmdc}$ Din păcate, nu putem calcula suma pe secvențe pentru aceste operații folosind tehnica sumelor parțiale. Pentru a rezolva problema asta există structuri de date mai avansate, cum ar fi Sparse Tables. Însă, putem calcula minime, maxime și $\mathrm{cmmdc}$uri pe prefixe și sufixe fără nicio problemă.

Probleme recomandate

Pe lângă problemele din acest articol, pe care în marea lor parte le puteți găsi pe PbInfo, puteți lucra următoarele probleme de pe InfoArena:

• Divk
• Flori5
• Grădina3
• Livada3

Recomand să citiți și articolul despre tehnica Two-Pointers, prin intermediul căreia putem rezolva mai ușor cazuri particulare ale unor probleme din acest articol. Dacă aveți vreo întrebare legată de sume parțiale, nu ezitați să o lăsați într-un comentariu mai jos, pentru a vă putea ajuta