
Admitere Informatică Iași 2016 – Subiecte și rezolvări
În acest articol voi prezenta rezolvările subiectelor date în anul 2016 la admitere la Facultatea de Informatică din Iași. (Aici puteți găsi baremul, însă e foarte sumar.) Dacă sunteți interesați de subiectele din 2017, le găsiți rezolvate aici, iar pe cele din 2018 aici.
Subiectul I. Problema 1.
Un număr natural desemnează un an bisect dacă este multiplu de dar nu este multiplu de cu excepția numerelor multiplu de De exemplu și sunt ani bisecți, dar și nu sunt ani bisecți. Care dintre expresiile C++ de mai jos testează dacă valoarea variabilei desemnează un an bisect?
(n % 100 != 0) && (n % 4 == 0)(n % 4 == 0) && ((n % 100 != 0) || (n % 400 == 0)(n % 100 != 0) || (n % 4 == 0)(n % 4 == 0) && ((n % 100 != 0) && (n % 400 == 0))
Prima expresie nu este corectă pentru că returnează false pentru multiplii lui din cauza primei condiții. A doua expresie e corectă – este exact definiția unui an bisect tradusă în C++. A treia expresie este greșită pentru că, de exemplu, returnează true pentru numărul din cauza primei condiții. A patra expresie e o aberație, pentru că un număr nu poate fi divizibil cu și cu nu. Deci, varianta corectă este B.
Subiectul I. Problema 2.
Se consideră subprogramul recursiv de mai jos, descris în pseudocod. Subprogramul primește ca parametri două numere naturale și și întoarce un număr natural. Operația
%reprezintă restul împărțirii, iarmax(a, b)reprezintă maximul dintre șia) Care este valoarea returnată de subprogram pentru parametrii și
b) Dați exemplu de două numere naturale distincte și nenule astfel încât să returneze
Rolul cerinței precedente este să ne dăm seama ce face de fapt funcția dată. În această problemă, se observă ușor că ea calculează într-un mod mai ciudat: Dacă ambele numere sunt pare, le putem înjumătăți, și vom ști că ul lor este de două ori mai mare decât ul noilor numere. Dacă un număr este par și celălalt impar, îl putem înjumătăți pe cel par, pentru că factorul nu se găsește și în celălalt, așa că nu va influența ul lor. Dacă ambele numere sunt impare se aplică algoritmul clasic de determinare a ului prin scăderi repetate, într-o formă recursivă. Deci, un posibil răspuns pentru această cerință este și căci
c) Dacă care este cea mai mare valoare strict mai mică decât pentru astfel încât să returneze
Avem nevoie de cel mai mare multiplu de mai mic decât care nu e divizibil cu (Dacă ar fi divizibil și cu ar fi multiplu de caz în care ar deveni Răspunsul e
d) Scrieți funcția C++ corespunzătoare subprogramului dat.
Un răspuns posibil este:
int F(int u, int v) { if (u == v || !u || !v) return u > v ? u : v; if (u % 2 == 0) { if (v % 2 == 0) return 2 * F(u / 2, v / 2); return F(u / 2, v); } if (v % 2 == 0) return F(u, v / 2); if (u < v) return F(u, (v - u) / 2); return F((u - v) / 2, v);}Subiectul II. Problema 1.
Care este înălțimea maximă a unui arbore cu rădăcină, având noduri, știind că fiecare nod intern (care nu este rădăcină sau frunză) are mai multe noduri fiu decât părintele său? (Înălțimea arborelui este numărul de muchii ale celui mai lung drum de la rădăcină la o frunză.)
- Nu există un astfel de arbore
Vom construi arborele astfel: Atribuim un singur fiu rădăcinii, notată cu Acest nod va trebui să aibă minim doi fii ca să respecte condiția din enunț. Din acești doi fii, pe îl vom lăsa să fie frunză, și extindem arborele doar prin căruia trebuie să-i atribuim trei fii Din nou vom încerca să lăsăm cât mai multe frunze, așa că vom continua să adăugăm fii doar la Acesta trebuie să aibă măcar patru fii Adăugându-i pe aceștia, am terminat de construit arborele cerut cu noduri:
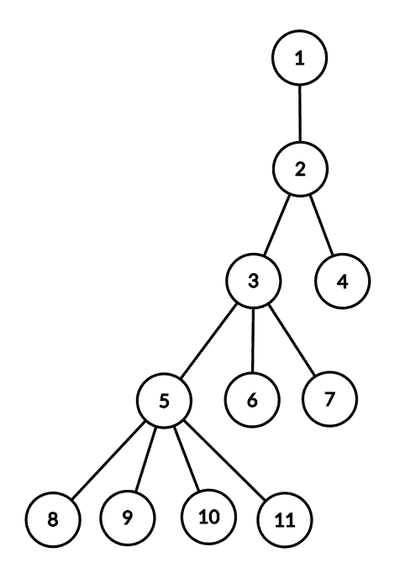
Se poate observa că înălțimea lui este Varianta corectă este așadar B.
Subiectul II. Problema 2.
Fie un graf neorientat în care fiecare nod are un număr par și nenul de vecini, astfel încât nu există două noduri având același număr de vecini. Care dintre următoarele variante ar putea reprezenta numărul de muchii ale unui astfel de graf?
- Nu există un astfel de graf
Dacă veți încerca să desenați un astfel de graf, veți vedea că trebuie adăugate noduri la infinit pentru a le asigura numărul minim de vecini astfel încât să respecte condițiile problemei. Varianta corectă este D, iar justificarea este că gradele minime ale unui graf cu noduri ar trebui să fie Însă, gradul maxim al unui nod într-un graf neorientat este și se obține atunci când „legăm” un nod de toate celelalte noduri. Nu există niciun număr natural pentru care așa că putem afirma că nu există un graf de acest tip.
Subiectul II. Problema 3.
Considerăm un șir oarecare format doar din caractere din mulțimea Mulțimea
definește regulile de transformare care pot fi aplicate unui astfel de șir. Fiecare dintre aceste transformări, aplicată unui șir de caractere oarecare, va înlocui prima apariție a subșirului de trei caractere din partea stângă a regulii, cu subșirul din partea dreaptă. Pornind de la șirul inițial, vom aplica în mod repetat oricare dintre transformările din mulțimea atât timp cât acest lucru este posibil.
Exemplu: Pentru șirul de caractere o secvență posibilă de aplicare a regulilor este:
a) Demonstrați că, indiferent de șirul considerat inițial și indiferent de ordinea de aplicare a regulilor de transformare, după un număr finit de pași se va obține un șir ce conține pe fiecare poziție doar caracterul
În primul rând, se observă că orice transformare conduce la formarea unui șir mai mic lexicografic, de aceeași lungime ca cel precedent. Asta înseamnă că după fiecare transformare aplicată șirului dat, vom fi tot mai aproape de șirul format doar din În al doilea rând, știm că nu există niciun șir în care ne putem „bloca”, pentru că fiecare șir de lungime diferit de are asociată o regulă de transformare. Așadar, întotdeauna vom putea ajunge la un șir ce conține pe fiecare poziție caracterul
Observație: În enunț ar fi trebuit pusă totuși o restricție legată de lungimea șirului. Aceasta ar trebui să fie minim căci altfel n-am putea aplica nicio transformare asupra lui.
b) Scrieți un program C++ care:
- Citește de la tastatură un șir format doar din caracterele și În cazul în care șirul conține și alte caractere, va fi afișat mesajul
"Date invalide".- Pornind de la șirul aplică toate regulile de transformare din mulțimea atât timp cât este posibil și afișează numărul de aplicări ale acestor reguli.
- Verifică faptul că șirul rezultat în final este format doar din caractere egale cu
Mai jos puteți vedea soluția mea însoțită de comentarii.
#include <iostream>using namespace std;
// Fie 100 lungimea maximă a șirului inițial.const int SMAX = 101;
int cnt; // numărul de transformări aplicatechar str[SMAX]; // șirul dat
// matrice cu regulile de transformarechar R[8][4] = {"aaa", "aaa", "aab", "aba", "abb", "aba", "baa", "bab"};
int main() { // Citim și validăm șirul: cin >> str; for (int i = 0; str[i]; i++) if (str[i] != 'a' && str[i] != 'b') { cout << "Date invalide\n"; return 0; }
// Aplicăm transformările: bool ok; do { ok = false; for (int i = 2; str[i]; i++) { // Căutăm o secvență de lungime 3 pe care o putem transforma. int ind = (str[i] - 'a') + 2 * (str[i - 1] - 'a') + 4 * (str[i - 2] - 'a'); str[i - 2] = R[ind][0]; str[i - 1] = R[ind][1]; str[i] = R[ind][2]; if (ind) { // Dacă secvența nu era "aaa": cnt++; ok = true; } } } while (ok);
// Afișăm numărul de transformări efectuate, // și verificăm dacă toate caracterele șirului curent sunt 'a': cout << cnt << '\n'; for (int i = 0; str[i]; i++) if (str[i] != 'a') { cout << "Sirul final nu este format doar din caractere egale cu a.\n"; return 0; } cout << "Sirul final este format doar din caractere egale cu a.\n"; return 0;}Pentru a reține regulile convenabil am declarat o matrice de tip char cu linii și coloane. Pe fiecare linie am reținut câte o regulă de transformare, pe linia având o regulă „fictivă”, care transformă șirul în Matricea trebuie să aibă minim coloane deoarece pentru inițializarea liniilor am folosit constante de tipul șir de caractere, care au și ele nevoie de loc pentru terminatorul nul. Dacă în schimb am fi inițializat fiecare caracter al matricei în parte, ar fi fost suficiente și linii.
Pentru a înțelege cum am aplicat transformările, trebuie menționat că al lea șir din este chiar numărul scris în baza însemnând și Ca să aplic transformările am utilizat un algoritm asemănător cu Bubble Sort: În do-while parcurg vectorul, iar pentru fiecare calculez în linia pe care se află regula ce transformă secvența formată din caracterele de pe pozițiile și din str. Ca să fac asta, convertesc secvența într-un număr scris în baza După aceea, pur și simplu copiez caracterele din în și Repet procesul cât timp am efectuat măcar o transformare asupra șirului. Verificarea de la finalul programului este inutilă din cauza demonstrației de la punctul a. Dar dacă în enunț zice s-o facem, trebuie făcută!
Subiectul II. Problema 4.
Fie și două mulțimi de simboluri, ambele având același număr de elemente unde este un număr natural impar. Un pătrat este o matrice pătratică de dimensiune ce îndeplinește următoarele condiții:
- C1. Fiecare element al matricei este o pereche unde și
- C2. Pentru orice două elemente și aflate pe poziții diferite în matrice dar pe aceeași linie sau pe aceeași coloană, avem și
- C3. Pentru orice două elemente și aflate pe poziții diferite în matrice, avem sau
Exemplu: Pentru și un pătrat posibil este:
a) Dați un exemplu de pătrat pentru și
O strategie simplă de a genera o astfel de matrice se poate deduce chiar din exemplul lor: Pe prima linie scriem perechile Pentru fiecare dintre liniile următoare copiem linia precedentă, dar cu literele permutate circular cu o poziție la dreapta, iar cifrele la stânga.
b) Scrieți o funcție C++ care primește ca argumente numărul natural impar și două tablouri de caractere, reprezentând mulțimile și și construiesc un pătrat.
Cum în enunț matricea pe care trebuie să o construim nu este inclusă în lista de parametri, iar funcțiile nu pot returna tablouri, am declarat global o matrice mat. Aceasta conține elemente de tipul Pair, care este un struct definit de mine cu două câmpuri: x și y. În rest nu prea am ce comenta, funcția f construiește matricea exact după procedeul descris la cerința anterioară.
// (NMAX - 1) = valoarea maximă a lui n// Indexăm matricea și tablourile S și T de la 1.const int NMAX = 101;
struct Pair { char x, y;} mat[NMAX][NMAX]; // matricea construită de f()
void f(int n, char S[], char T[]) { for (int j = 1; j <= n; j++) { mat[1][j].x = S[j]; mat[1][j].y = T[j]; } for (int i = 2; i <= n; i++) { mat[i][1].x = mat[i - 1][n].x; for (int j = 2; j <= n; j++) mat[i][j].x = mat[i - 1][j - 1].x; mat[i][n].y = mat[i - 1][1].y; for (int j = 1; j < n; j++) mat[i][j].y = mat[i - 1][j + 1].y; }}c) Argumentați faptul că pătratul construit de funcția de la punctul b îndeplinește condițiile C1, C2 și C3.
Condiția C1 este îndeplinită trivial, pentru că pe prima linie a matricei punem în câmpurile elemente din în câmpurile elemente din iar restul liniilor folosesc elemente de pe liniile precedente. Condiția C2 se verifică și ea ușor: Elementele de pe orice linie sunt o permutare a vectorilor respectiv elementele fiind clar distincte. Fiind vorba de permutări circulare, și coloanele vor fi de fapt niște permutări circulare, deci și ele respectă această condiție.
Condiția C3 se demonstrează mai greu însă. Pentru ca două elemente de pe poziții diferite să fie egale, trebuie ca în primul rând câmpurile lor să fie la fel. Observăm că fiecare element din apare pe o diagonală paralelă cu diagonala principală. (De fapt pe două, dacă nu este vorba chiar de cea principală, însă ne putem imagina că acestea formează una singură.) Acum trebuie să căutăm două elemente de pe această diagonală cu urile egale, însă nu vom găsi! Asta pentru că pe fiecare diagonală de genul ăsta apare chiar o permutare a lui elementele crescând din în
Să luăm un exemplu concret – matricea de la punctul a:
Am îngroșat diagonala pe care se află litera Cifrele de pe această diagonală apar de sus în jos în ordinea După urmează și după urmează pentru că parcurgerea lui se ia de la capăt când se ajunge la final. Cum ul este impar și cifrele cresc din în ele nu se vor repeta. Dacă în schimb ul ar fi fost par, să zicem cifrele ar fi fost așa că (cel puțin) strategia noastră de completare a matricei n-ar mai fi funcționat.
Subiectul III. Problema 1.
Se consideră toate șirurile de lungime formate din și Câte dintre acestea au proprietatea că suma oricăror elemente de pe poziții consecutiive este
Ideea de bază este că dacă avem fixați primii termeni ai șirului, celelalte elemente sunt determnate în mod unic: Analizăm pe rând fiecare secvență de lungime Observăm că pentru a trece de la o secvență la următoarea, trebuie să eliminăm primul element din stânga și să inserăm unul nou la dreapta, astfel încât suma elementelor noii secvențe să fie Dacă elementul eliminat este suma elementelor rămase devine așa că trebuie să adăugăm neapărat pentru a reveni la suma Dacă elementul eliminat este suma rămâne așa că trebuie să adăugăm tot pentru a nu o modfica.
Acum că am demonstrat asta, putem spune că numărul de șiruri cu proprietatea dată este egal cu numărul de șiruri binare de lungime cu suma elementelor Adică numărul de șiruri de lungime formate din elemente de și elemente de Acesta este egal cu Prin urmare, varianta corectă este A.
Subiectul III. Problema 2.
John McCarthy, unul dintre fondatorii domeniului inteligență artificială, a propus funcția definită mai jos și numită funcția 91 a lui McCarthy. Ce valoare va returna apelul
Trebuie doar să urmărim lanțul de apeluri recursive. Pentru a nu ne încurca, am schimbat numele funcției în simplu…
F( 91) = F(F( 91 + 11 = 102)) =F( 92) = F(F( 92 + 11 = 103)) =F( 93) = F(F( 93 + 11 = 104)) =F( 94) = F(F( 94 + 11 = 105)) =F( 95) = F(F( 95 + 11 = 106)) =F( 96) = F(F( 96 + 11 = 107)) =F( 97) = F(F( 97 + 11 = 108)) =F( 98) = F(F( 98 + 11 = 109)) =F( 99) = F(F( 99 + 11 = 110)) =F(100) = F(F(100 + 11 = 111)) =F(111) = 91Subiectul III. Problema 3.
Fie o matrice de numere naturale cu linii și coloane. O secvență de pe poziții din se numește progresivă dacă șirurile
sunt progresii aritmetice cu rații nenule. De exemplu, în matricea
este evidențiată secvența progresivă Indicii liniilor sunt în progresie aritmetică de rație nenulă, indicii coloanelor sunt în progresie aritmetică de rație nenulă, iar valorile sunt și ele în progresie aritmetică de rație nenulă.
a) Pentru matricea de mai jos, scrieți care este cea mai lungă secvență progresivă. Dacă sunt mai multe astfel de secvențe, alegeți oricare dintre ele.
O secvență progresivă de lungime maximă din matricea dată este
Cealaltă variantă se obține scriind această secvență în ordine inversă. Evident că dacă o secvență este progresivă, atunci și „inversa” ei este progresivă, pentru că doar rațiile s-ar schimba (s-ar înmulți cu
b) Scrieți o funcție C++ care primește ca parametri dimensiunile și ale matricei, matricea și primele două poziții dintr-o secvență progresivă din Funcția va returna lungimea secvenței progresive din ce începe cu și care are un număr maxim de elemente.
Presupunem că pozițiile date reprezintă un început valid de secvență progresivă, și anume că rațiile formate sunt nenule. Mai întâi calculez în iR, jR și xR rațiile liniilor, coloanelor și ale elementelor. Apoi, folosind un for destul de complex (dar logic), incrementez lungimea secvenței cât timp elementele selectate continuă să se afle în progresie aritmetică.
// (NMAX - 1) = valoarea maximă a lui N// (MMAX - 1) = valoarea maximă a lui M
int maxLen(int N, int M, int A[NMAX][MMAX], int i1, int j1, int i2, int j2) { int iR = i2 - i1; int jR = j2 - j1; int xR = A[i2][j2] - A[i1][j1]; int len = 2; for (int i = i2 + iR, j = j2 + jR; 1 <= i && i <= N && 1 <= j && j <= M && A[i][j] == A[i - iR][j - jR] + xR; i += iR, j += jR) len++; return len;}c) Scrieți o funcție C++ care primește ca parametri dimensiunile și ale matricei și matricea Funcția va returna lungimea secvenței progresive din care are un număr maxim de elemente. În rezolvare, puteți apela funcția de la punctul b.
Din moment ce în enunț se specifică faptul că putem folosi funcția precedentă, este destul de clar că trebuie pur și simplu să alegem toate începuturile posibile de secvență progresivă, să calculăm lungimea fiecăreia, iar la final să returnăm maximul obținut. Trebuie să avem grijă ca fiecare pereche de poziții de start să fie validă, adică să nu formeze vreo rație zero. Este posibil să nu existe nicio pereche validă de poziți de start, caz în care trebuie returnat 1. Am tratat acest caz inițializând variabila sol cu 1.
int maxLen(int N, int M, int A[NMAX][MMAX]) { int sol = 1; for (int i1 = 1; i1 <= N; i1++) for (int j1 = 1; j1 <= M; j1++) for (int i2 = 1; i2 <= N; i2++) if (int i2 != i1) for (int j2 = 1; j2 <= M; j2++) if (int j2 != j1 && A[i1][j1] != A[i2][j2]) { int len = maxLen(N, M, A, i1, j1, i2, j2); if (len > sol) sol = len; } return sol;}Se vede clar că algoritmul are o complexitate de ordinul Am putea face o mică optimizare, și anume să folosim observația de la punctul a pentru a nu parcurge de două ori aceeași secvență din direcții diferite. Dar complexitatea rămâne aceeași, așa că nu are sens să ne complicăm.
Astea au fost subiectele de la admitere din 2016. Mie mi s-au părut ceva mai grele decât cele din 2017 și 2018, în special datorită cerinței II.4.2 și a argumentării răspunsului de la problema II.2. (Chiar dacă subiectul spune doar să scrieți litera corespunzătoare răspunsului corect, se punctează și justificarea.) Dacă aveți vreo întrebare legată de problemele din acest articol, nu ezitați să lăsați un comentariu mai jos