Elemente de combinatorică: Permutări, Aranjamente, Combinări

Combinatorica este ramura matematicii care se ocupă în principal de numărarea modurilor în care pot fi alese anumite obiecte, respectând anumite condiții. În acest articol voi prezenta cele trei elemente de bază ale combinatoricii, precum și câteva aplicații ale acestora. Pentru simplitate, ne vom referi doar la mulțimi finite de forma $M = \{1, 2, \ldots, n\}$ cu $n \in \mathbb{N}$ Dar mai întâi trebuie să amintesc cele două reguli fundamentale folosite în problemele de numărare:

Regula sumei

Dacă avem două mulțimi disjuncte $A$ și $B$ cu $m$ și respectiv $n$ elemente, numărul de moduri de a alege un element din $A$ sau din $B$ este $m + n$ Cu alte cuvinte, reuniunea mulțimilor $A$ și $B$ are $m + n$ elemente.

Regula produsului

Dacă avem două mulțimi $A$ și $B$ cu $m$ și respectiv $n$ elemente, numărul de moduri de a alege un element din $A$ și unul din $B$ este $m \cdot n$ Cu alte cuvinte, produsul cartezian al mulțimilor $A$ și $B$ are $m \cdot n$ elemente.

Permutări

Din punct de vedere combinatorial, o permutare a unei mulțimi reprezintă o modalitate de a aranja secvențial elementele acesteia. De exemplu, permutările mulțimii $A = \{1, 2, 3\}$ sunt:

Permutările unei mulțimi $A$ pot fi privite de asemenea drept totalitatea funcțiilor bijective definite pe $A$ cu valori în $A$ Asta e ușor de înțeles dacă ne gândim că $f(x)$ nu trebuie să fie neapărat o expresie ce-l conține pe $x$ ci îl putem defini folosind o înșiruire de pentru-uri. De exemplu, a treia permutare de mai sus reprezintă funcția:

Numărul permutărilor de ordin $n$ (permutările unei mulțimi $A$ cu $n$ elemente) se notează cu $P_n$ și este egal cu $n!$ (Amintesc că $n!$ se citește $n$ factorial și este egal cu $1 \cdot 2 \cdot 3 \cdots n$ Această relație poate fi demonstrată în mai multe moduri. Să analizăm două dintre ele:

Metoda 1

Atunci când vrem să construim o permutare de ordin $n$ pe prima poziție putem pune orice valoare de la $1$ la $n$ deci avem $n$ variante. Pentru a doua poziție, ne-au rămas $n - 1$ variante, pentru că deja am folosit una dintre valori pentru prima poziție. Pentru a treia poziție, am rămas cu $n - 2$ variante, pentru că deja am folosit două elemente pentru primele două poziții. Generalizând raționamentul, pentru poziția $i$ $\htmlClass{katexified}{(} 1 \le i \le n$ avem $n - i + 1$ variante rămase. Aplicând regula produsului, obținem:

Metoda 2

Vom demonstra prin inducție matematică relația $P_n = n!$ Dacă avem o permutare de ordin $k$ și vrem să obținem din aceasta una de ordin $k + 1$ nu avem decât să inserăm undeva în ea valoarea $k + 1$ Aceasta poate fi inserată înainte de o poziție $i$ cu $1 \le i \le k$ sau după ultima poziție. În total avem $k + 1$ poziții posibile pentru noul element. Conform regulii produsului, obținem $P_{k + 1} = (k + 1) \cdot P_k$ de unde $P_n = n!$

Permutări cu repetiție

Când vine vorba să numărăm permutările unui șir ale cărui elemente nu sunt neapărat distincte, formula clasică de la permutări nu mai funcționează. De exemplu, pe o permutare de genul $\langle 1, 3, 2, 3 \rangle$ am număra-o de două ori, ca și cum cei doi de $3$ ar fi numere diferite. O dată cu primul $3$ pe poziția $2$ și al doilea $3$ pe poziția $4$ și o dată cu al doilea $3$ pe poziția $2$ și primul $3$ pe poziția $4$

Deci, dacă notăm cu $f(i)$ frecvența (numărul de apariții al) numărului $i$ în permutare, atunci pentru fiecare $i$ din șirul $a$ am numărat de $P_{f(i)}$ ori mai multe permutări decât trebuia. Așadar, formula pentru numărul de permutări cu repetiție ale unui șir $a$ de lungime $n$ cu elementele mai mici sau egale cu $n$ este:

Aranjamente

Un aranjament de $n$ elemente luate câte $k$ al mulțimii $A$ de cardinal $n$ reprezintă o submulțime ordonată a lui $A$ de $k$ elemente. De exemplu, aranjamentele de $3$ luate câte $2$ ale mulțimii $A = \{1, 2, 3\}$ sunt:

Similar permutărilor, aranjamentele pot fi considerate funcții injective definite pe mulțimea $\{1, 2, \ldots, k\}$ cu valori în $\{1, 2, \ldots, n\}$ Semnificația expresiei $f(x) = y$ este că elementul de pe poziția $x$ din aranjament este egal cu $y$ Cred că deja e clar că permutările sunt un caz particular de aranjamente: Permutările de ordin $n$ sunt aranjamente de $n$ luate câte $n$

Numărul aranjamentelor de $n$ luate câte $k$ se notează cu $A_n^k$ și este egal cu $\frac{n!}{(n - k)!}$ Din nou, putem demonstra această relație în două moduri:

Metoda 1

Atunci când construim un aranjament de $n$ elemente luate câte $k$ pe prima poziție putem pune orice valoare, deci avem $n$ variante. Pe a doua poziție putem pune orice valoare, mai puțin cea pe care deja am folosit-o, deci am rămas cu $n - 1$ variante. Generalizând, obținem:

Metoda 2

Putem construi aranjamentele de $n$ elemente luate câte $k$ pornind de la permutările de ordin $n$ Pentru asta, este de ajuns să ștergem ultimele $n - k$ elemente din fiecare permutare, însă nu vom rămâne cu aranjamente distincte. De exemplu, dacă $n = 5$ și $k = 2$ permutările care se transformă în aranjamentul $(3, 1)$ sunt:

Se observă ușor că numărul de permutări care generează un anumit aranjament este $P_{n - k}$ pentru că ultimele $n - k$ elemente ale lor pot fi aranjate în $P_{n - k}$ moduri. Așadar, $A_n^k = \frac{P_n}{P_{n - k}} = \frac{n!}{(n - k)!}$

Combinări

Combinările de $n$ elemente luate câte $k$ ale mulțimii $A$ de cardinal $n$ reprezintă submulțimile cu $k$ elemente ale lui $A$ De remarcat că submulțimile nu sunt ordonate, ceea ce înseamnă că, în cazul combinărilor, submulțimile $\{1, 2, 3\}$ și $\{2, 3, 1\}$ nu sunt diferite. De exemplu, combinările de $4$ luate câte $3$ ale mulțimii $A = \{1, 2, 3, 4\}$ sunt:

Numărul de combinări de $n$ luate câte $k$ se notează cu $C_n^k$ și este egal cu $\frac{n!}{k!(n - k)!}$ Demonstrația este următoarea: Diferența dintre aranjamente și combinări este că aranjamentele sunt submulțimi ordonate. Deci, o combinare de lungime $k$ corespunde aranjamentelor de lungime $k$ formate permutând elementele respectivei combinări. Numărul acelor permutări este $P_k$ de unde $C_n^k = \frac{A_n^k}{P_k} = \frac{n!}{k!(n - k)!}$

Cum combinările numără submulțimile unei mulțimi în funcție de cardinalul lor, suma combinărilor de $n$ luate câte $k$ cu $0 \le k \le n$ este egală cu numărul total de submulțimi ale unei mulțimi de cardinal $n$ Acesta este $2^n$ deoarece pe fiecare element putem fie să-l luăm, fie să nu-l luăm în cadrul submulțimii, așa că pentru fiecare element avem două variante. Aplicând regula produsului, obținem $\underbrace{2 \cdot 2 \cdots 2}_{\text{de } n \text{ ori}} = 2^n$

Triunghiul lui Pascal

Triunghiul lui Pascal se referă la aranjamentul geometric pe care-l obținem când scriem pe fiecare linie $n \ge 0$ numerele $C_n^k$ unde $k$ ia valori pe rând de la $0$ la $n$

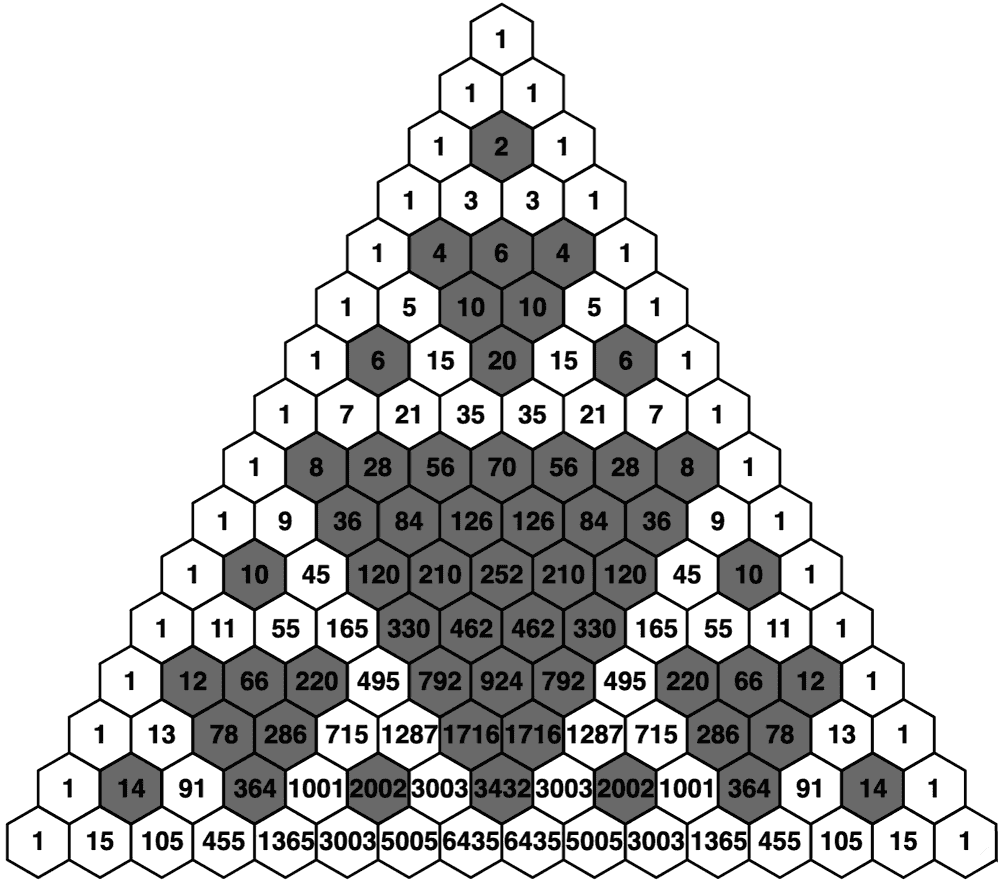
Acest desen ne ajută să vizualizăm mai ușor diverse proprietăți ale combinărilor. De exemplu, dacă colorăm cu gri combinările pare, obținem Triunghiul lui Sierpinski, ceea ce am ilustrat și în desenul de mai sus. O altă observație este că $C_n^k = C_n^{n - k}$ Poate fi demonstrată imediat folosind formula cu factoriale: $\frac{n!}{k!(n - k)!} = \frac{n!}{(n - k)!k!}$

Poate cea mai importantă proprietate a combinărilor ce rezultă din Triunghiul lui Pascal este următoarea relație de recurență:

Ea ne permite să precalculăm toate combinările până la linia $n$ în $O(n^2)$ – complexitate, evident, optimă, fiind egală cu dimensiunea output-ului:

comb[0][0] = 1;
for (int i = 1; i <= n; i++) {
    comb[i][0] = 1;
    for (int j = 1; j <= i; j++)
        comb[i][j] = comb[i - 1][j - 1] + comb[i - 1][j];
}

Recurența poate fi demonstrată relativ ușor folosind din nou formula cu factoriale:

Însă nu e o metodă suficient de interesantă sau de ușoară la calcule. O prefer pe cea constructivă, pentru că ne obișnuiește cu gândirea specifică problemelor de programare dinamică: Fie mulțimile $A = \{1, 2, \ldots, n\}$ și $B = \{1, 2, \ldots, n - 1\}$ Putem construi o combinare a lui $A$ de $k$ elemente, adăugându-l pe $n$ la o combinare de $k - 1$ elemente a mulțimii $B$ Însă, nu toate combinările trebuie sa-l conțină pe $n$ Observăm că cele din urmă sunt combinări de $k$ elemente ale lui $B$ Cum cele două tipuri de combinări menționate sunt numărate de $C_{n - 1}^{k - 1}$ și respectiv de $C_{n - 1}^{k}$ aplicând regula sumei, obținem recurența ce trebuia demonstrată.

O altă formulă ce poate fi dedusă din Triunghiul lui Pascal este aceasta:

Și se demonstrează așa:

Nu știu cât de utilă pare, dar eu chiar am avut nevoie de ea la un moment dat într-o problemă.

Binomul lui Newton

Combinările se mai numesc coeficienți binomiali, deoarece se regăsesc drept coeficienți în descompunerea lui $(a + b)^n$ $\htmlClass{katexified}{(} n \in \mathbb{N}$ numit Binomul lui Newton:

În ciuda aparențelor, Binomul lui Newton este util și la informatică! L-am folosit odată la problema Scara2 pentru a demonstra că dinamica avea de fapt complexitatea $3^n$ și nu $4^n$ cum credeam inițial.

Demonstrația formulei se bazează pe inducție: Presupunem că $(a + b)^n$ are forma de mai sus și demonstrăm că, înmulțind expresia cu $a + b$ obținem o descompunere de aceeași formă:

Grupăm termenii asemenea, aplicăm coeficienților acestora formula de recurență a combinărilor și înlocuim $C_n^0$ cu $C_{n + 1}^0$ și $C_n^n$ cu $C_{n + 1}^{n + 1}$ căci toate sunt egale cu $1$

Notă: Prin convenție, $0! = P_0 = A_n^0 = C_n^0 = 1$ unde $n \in \mathbb{N}$ Cea mai simplă explicație este că $1$ e elementul neutru la înmulțire. Iar în lipsa acestei convenții, formulele n-ar mai funcționa.

Cam atât despre permutări, aranjamente și combinări. Urmează în curând un articol despre numărul partițiilor unui număr natural! Dacă aveți vreo întrebare despre combinatorică, nu ezitați să o lăsați mai jos, într-un comentariu