$Desenarea fractalilor în P5.JS. Top 7 fractali!$

Desenarea fractalilor în P5.JS. Top 7 fractali!

de Iulian Oleniuc | 06/08/2020 | Diverse

Un fractal este o figură geometrică ce poate fi divizată în mai multe părți, astfel încât fiecare dintre acestea să fie o copie în miniatură a originalului. Câteva exemple naturale de fractali sunt ferigile, fulgii de zăpadă, cochiliile de melci și fulgerele. De obicei, definiția fractalilor este simplă și recursivă.

Fractalii mi se par fascinanți, și cred că sunt un mod plăcut de a aprofunda conceptul de recursivitate (mai exact metoda Divide et Impera). Prin urmare, în acest articol vom învăța să desenăm câțiva fractali faimoși în JavaScript, folosind biblioteca grafică P5.JS. Am ales combinația asta pentru că P5.JS e mult mai intuitiv decât orice bibliotecă grafică pentru C++, iar sintaxa JavaScript simplifică și mai mult partea de programare.

Cuprins

Articolul a ieșit mult mai lung decât mă așteptam, așa că, pentru prima dată, sunt nevoit să-i alcătuiesc un cuprins:

Introducere în P5.JS

Pentru a începe să creăm folosind P5.JS avem nevoie doar de o pagină HTML și de un fișier JavaScript. Pagina index.html trebuie să conțină doar câteva linii de cod pentru includerea scripturilor JS de care avem nevoie. Primul script este biblioteca P5.JS, care poate fi livrată direct de un CDN (vedeți URL-ul de mai jos), iar al doilea este scriptul nostru, sketch.js. Mai multe detalii despre set-up găsiți aici.

index.html
<html>
  <head>
    <script src="https://cdn.jsdelivr.net/npm/p5@1.1.9/lib/p5.js"></script>
    <script src="sketch.js"></script>
  </head>
</html>

Dacă vă este lene să creați cele două fișere, puteți accesa editorul lor online. Când terminați de codat, apăsați butonul sub formă de triunghi din stânga-sus, iar în dreapta veți putea vedea rezultatul.

În fișierul sketch.js trebuie să definim obligatoriu două funcții: setup și draw. Funcția setup este apelată o singură dată, la începutul rulării scriptului, și are rolul de a pregăti pânza de desenare (canvas-ul). Primul lucru pe care trebuie să-l facem în funcția setup este să creăm canvas-ul și să-i setăm dimensiunile. Asta se face prin apelul createCanvas(w, h), unde w este lățimea și h înălțimea. Dimensiunile se specifică în pixeli.

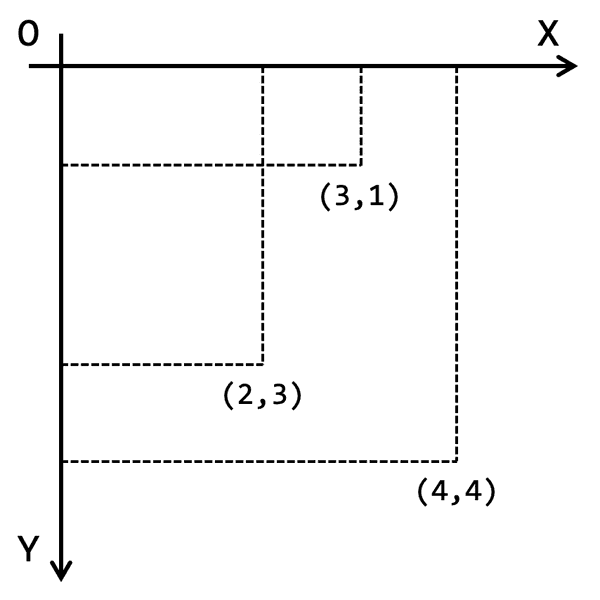
Un alt aspect ce trebuie menționat este modul în care sunt dispuse axele de coordoante. Axa $OX$ corespunzătoare lățimii, este orientată la dreapta, pe când axa $OY$ corespunzătoare înălțimii, este orientată în jos. Originea sistemului cartezian se află în colțul din stânga-sus al canvas-ului. Convenția asta e valabilă cam pentru tot ceea ce înseamnă grafică pe calculator, iar avantajele sunt similare cu cele ale scrisului de la stânga la dreapta și de sus în jos.

Funcția draw este apelată de fiecare dată când se redesenează canvas-ul. FPS-ul implicit este egal cu cel al display-ului vostru, deci probabil $60$ de frame-uri pe secundă. De obicei, primul lucru pe care-l facem în funcția draw este să colorăm fundalul, folosind funcția background. Astfel, desenele făcute la frame-ul precedent vor fi șterse.

Prima animație

În continuare, vom crea prima noastră animație, ca să mai învățăm niște lucruri de bază. Iată mai jos un script care, la fiecare frame, desenează un cerc în jurul cursorului. Cercul este galben, iar fundalul albastru.

sketch.js
function setup() {
  createCanvas(300, 300);
}

function draw() {
  background(20, 60, 220);
  fill(255, 255, 0);
  circle(mouseX, mouseY, 50);
}

Linia 2 creează un canvas de dimensiuni $300 \times 300$ Linia 6 colorează background-ul folosind culoarea $(20, 60, 220)$ Cele trei numere reprezintă nuanțele folosite de roșu, verde și respectiv albastru, pe o scară de la $0$ la $255$ Pentru a afla codul RGB al culorii pe care doriți să o folosiți, Google vă pune la dispoziție un instrument foarte intuitiv; dați un search cu html color picker pentru a-l accesa.

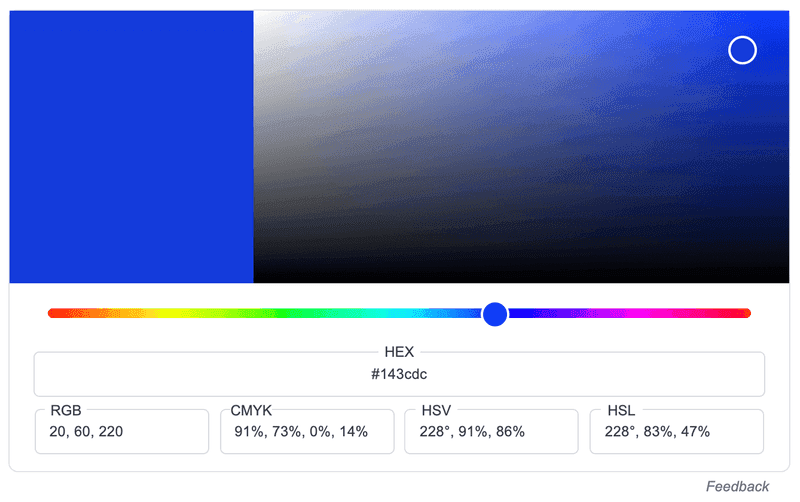
Linia 7 setează la galben culoarea ce urmează să fie folosită pentru umplerea formelor, pentru scrierea de text etc. Linia 8 desenează un cerc cu centrul de coordonate (mouseX, mouseY) și diametrul $50$ Numite sugestiv, mouseX și mouseY sunt niște variabile globale care ne dau coordonatele cursorului în cadrul canvas-ului.

Observații

Acum, câteva observații. Funcțiile legate de culori, printre care background și fill, pot lua unul, doi, trei sau patru parametri. Dacă o astfel de funcție e apelată cu trei parametri, aceștia reprezintă nuanțele de roșu, verde și albastru ale culorii respective. Dacă e apelată cu un singur parametru, atunci culoarea va fi o nuanță de gri (de la $0$ la $255$ Dacă la cele două cazuri precedente mai adăugăm un parametru, acela va reprezenta gradul de opacitate al culorii, tot de la $0$ la $255$ Iată ce efect interesant putem obține dacă setăm opacitatea background-ului sub $255$

Asta se întâmplă deoarece, atunci când recolorăm fundalul, folosim o culoare transparentă, așa că pe ecran rămân urme de la pozițiile anterioare ale cercului, care se șterg treptat. Apelul funcției background folosit mai sus este background(20, 60, 220, 50). Dacă n-am apela deloc funcția background, n-ar mai avea cine să șteargă cercul desenat la pasul precedent, obținându-se următorul efect:

Până acum, cercurile desenate aveau un contur. Dacă vrem să schimbăm culoarea sa, apelăm funcția stroke(culoare). Parametrii funcției stroke se transmit la fel ca la funcțiile background și fill. Dacă dorim să schimbăm grosimea conturului, apelăm funcția strokeWeight(grosime). Totuși, de obicei nu avem nevoie de contur. Așadar, dacă vrem să-l anulăm complet, apelăm funcția noStroke(). Dacă asta e o setare valabilă pentru toată execuția scriptului, o putem menționa foarte bine în funcția setup.

Cam atât despre culori și contur. Evident că mai sunt o grămadă de lucruri importante de spus despre P5.JS, dar vom vorbi despre ele la momentul potrivit. Când aveți neclarități legate de comportamentul unei funcții, sau când doriți să explorați biblioteca grafică, puteți consulta documentația oficială aici. Cred că ne putem apuca de treabă!

Triunghiul lui Sierpinski

Pentru a desena Triunghiul lui Sierpinski, pornim de la un triunghi negru, de preferință echilateral. Colorăm cu alb triunghiul median al triunghiului nostru, și repetăm procedeul pentru celelalte trei triunghiuri negre care se obțin. Triunghiul median al unui triunghi este determinat de mijloacele laturilor acestuia. Iată primele cinci iterații ale acestui fractal:

Variabila `MAX` și funcția `keyPressed`

În primul rând, avem nevoie de o variabilă globală MAX care să ne spună adâncimea maximă a arborelui de apeluri ale funcției noastre recursive de desenare. Adică, până la a câta iterație desenăm fractalul. Mi se pare o idee bună ca această variabilă să poată fi decrementată dând click în jumătatea stângă a canvas-ului, și respectiv incrementată dând click în dreapta. Vom seta valoarea maximă la $8$ iar pe cea minimă la $0$ iterația cu numărul $0$ fiind doar triunghiul negru inițial. Iată codul de până acum:

let MAX = 0;
function mousePressed() {
  if (mouseX < width / 2 && MAX > 0) MAX--;
  if (mouseX > width / 2 && MAX < 8) MAX++;
}

În JavaScript, variabilele se declară folosind keyword-ul let, indiferent de tipul lor de date. (Sintaxa cu var e cam învechită.) Dacă vrem ca o variabilă să nu-și schimbe valoarea pe parcursul execuției programului, o putem declara drept constantă, folosind keyword-ul const. Funcția mousePressed este apelată automat când dăm click în canvas.

Funcțiile `setup` și `draw`

Funcția setup creează un canvas de $300 \times 300$ și anulează conturul formelor prin noStroke():

function setup() {
  createCanvas(300, 300);
  noStroke();
}

În funcția draw colorăm background-ul folosind nuanța $70$ deci un gri închis. Apoi, setăm culoarea „pensonului” la $0$ (negru) și desenăm triunghiul mare, cu vârfurile în punctele de coordonate $(150, 39)$ $(22, 261)$ și $(278, 261)$ folosind funcția triangle. Se observă că nu are rost să desenăm triunghiuri negre în funcția recursivă; este de ajuns să desenăm unul singur, la început, pentru că atunci când ne mutăm recursiv la triunghiuri mai mici, ele vor fi deja negre.

Coordonatele punctelor au fost calculate în așa fel încât triunghiul să pară cât mai echilateral și să fie centrat în cadrul canvas-ului. Latura triunghiului are lungimea $2^8 = 256$ Am ales să fie o putere a lui $2$ ca de fiecare dată când împărțim o latură în două să obținem coordonate întregi… cel puțin în cazul bazei.

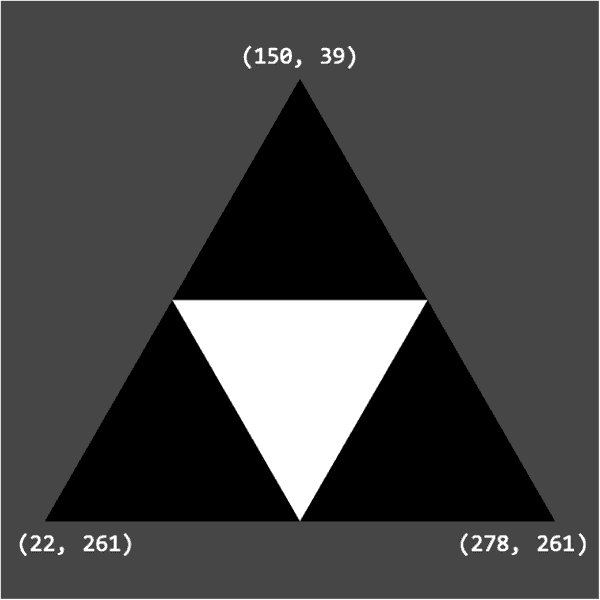
Urmează să setăm culoarea curentă la $255$ (alb) și să apelăm funcția recursivă de desenare, pe care o vom numi paint. Până să vorbim despre funcția asta, trebuie să mai spun ceva. Din cauza recursivității lui paint, funcția draw face cam multe operații pentru un frame rate de $60$ FPS: La numărul maxim de iterații se desenează $3^0 + 3^1 + \cdots + 3^7 = 3280$ de triunghiuri. Asta produce lag.

Putem rezolva foarte ușor problema asta dacă redesenăm fractalul numai atunci când modificăm variabila MAX. În acest sens, adăugăm un apel la funcția noLoop la finalul lui draw, oprind astfel redesenarea automată a cadrelor. Apoi, la finalul funcției mousePressed, apelăm funcția loop, pentru a reporni apelurile recurente ale lui draw.

Până acum, scriptul arată așa:

function setup() {
  createCanvas(300, 300);
  noStroke();
}

function draw() {
  background(70);
  fill(0);
  triangle(150, 39, 22, 261, 278, 261);
  fill(255);
  paint(...);
  noLoop();
}

let MAX = 0;
function mousePressed() {
  if (mouseX < width / 2 && MAX > 0) MAX--;
  if (mouseX > width / 2 && MAX < 8) MAX++;
}

Funcția `paint`

Urmează funcția recursivă paint, prin care desenăm fractalul. Aceasta ia ca parametri coordonatele vârfurilor triunghiului (x1, y1 – sus, x2, y2 – stânga, x3, y3 – dreapta) și iterația curentă (it). Deci, apelul inițial va fi paint(150, 39, 22, 261, 278, 261, 1). Primul lucru pe care-l facem în funcția paint este să ne oprim în caz că am depășit numărul maxim de iterații:

if (it > MAX) return;

Apoi, trebuie să calculăm mijloacele celor trei laturi ale triunghiului curent. Formula pentru coordonatele mijlocului unui segment se păstrează și în cazul sistemului cartezian cu susul în jos: Abscisa mijlocului e media aritmetică a absciselor extremităților, iar ordonata media ordonatelor.

const xMid1 = (x1 + x2) / 2, yMid1 = (y1 + y2) / 2;
const xMid2 = (x2 + x3) / 2, yMid2 = (y2 + y3) / 2;
const xMid3 = (x3 + x1) / 2, yMid3 = (y3 + y1) / 2;

Urmează să desenăm triunghiul median și să apelăm recursiv funcția paint pentru cele trei triunghiuri negre ce se formează în jurul lui. Prin it + 1 marcăm faptul că funcția trece la iterația următoare.

triangle(xMid1, yMid1, xMid2, yMid2, xMid3, yMid3);
paint(x1, y1, xMid1, yMid1, xMid3, yMid3, it + 1);
paint(xMid1, yMid1, x2, y2, xMid2, yMid2, it + 1);
paint(xMid3, yMid3, xMid2, yMid2, x3, y3, it + 1);

Gata! Mai jos aveți rezultatul și scriptul final.

Triunghiul lui Sierpinski
function setup() {
  createCanvas(300, 300);
  noStroke();
}

function draw() {
  background(70);
  fill(0);
  triangle(150, 39, 22, 261, 278, 261);
  fill(255);
  paint(150, 39, 22, 261, 278, 261, 1);
  noLoop();
}

function paint(x1, y1, x2, y2, x3, y3, it) {
  if (it > MAX) return;
  const xMid1 = (x1 + x2) / 2, yMid1 = (y1 + y2) / 2;
  const xMid2 = (x2 + x3) / 2, yMid2 = (y2 + y3) / 2;
  const xMid3 = (x3 + x1) / 2, yMid3 = (y3 + y1) / 2;
  triangle(xMid1, yMid1, xMid2, yMid2, xMid3, yMid3);
  paint(x1, y1, xMid1, yMid1, xMid3, yMid3, it + 1);
  paint(xMid1, yMid1, x2, y2, xMid2, yMid2, it + 1);
  paint(xMid3, yMid3, xMid2, yMid2, x3, y3, it + 1);
}

let MAX = 0;
function mousePressed() {
  if (mouseX < width / 2 && MAX > 0) MAX--;
  if (mouseX > width / 2 && MAX < 8) MAX++;
  loop();
}

Covorul lui Sierpinski

Pentru a desena Covorul lui Sierpinski, se pornește de la un pătrat negru, în centrul căruia se desenează un pătrat alb a cărui latură este de trei ori mai mică decât cea a pătratului mare. Procedeul se repetă pentru celelalte opt pătrate mici din jurul celui alb.

Pătrate în P5.JS

Mai întâi, trebuie să vedem cum se desenează un pătrat în P5.JS. Pentru a desena dreptunghiuri, există funcția rect (de la rectangle), care primește patru parametri. Aceștia pot fi interpretați în mai multe moduri: CORNER, CORNERS, CENTER, RADIUS. Modul implicit este CORNER, dar îl putem schimba folosind funcția rectMode(mod), unde mod ia o valoare dintre cele patru. Să analizăm cum sunt interpretați parametrii funcției rect(a, b, c, d) în fiecare caz:

CORNER: a și b – coordonatele colțului stânga-sus, c și d – lățimea și înălțimea
CORNERS: a și b – coordonatele colțului stânga-sus, c și d – coordonatele colțului dreapta-jos
CENTER: a și b – coordonatele centrului, c și d – lățimea și înălțimea
RADIUS: a și b – coordonatele centrului, c și d – jumătate din lățime și respectiv jumătate din înălțime

Cel puțin în cazul nostru, cred că cel mai adecvat mod este CENTER. Îl vom seta chiar în funcția setup:

function setup() {
  createCanvas(300, 300);
  rectMode(CENTER);
  noStroke();
}

Funcțiile `draw` și `paint`

Revenind la fractal, remarcăm din nou că este suficient să desenăm pătratul negru de la prima iterație. Acesta va fi centrat în cadrul canvas-ului și va avea lungimea laturii egală cu $3^5 = 243$ Am ales să fie putere a lui $3$ pentru că la fiecare pas împărțim latura pătratului curent la trei, și n-am vrea să obținem resturi. Înainte să vă uitați pe funcția draw, menționez că width și height sunt două variabile globale ce reprezintă dimensiunile canvas-ului:

function draw() {
  background(70);
  fill(0);
  rect(width / 2, height / 2, 243, 243);
  fill(255);
  paint(...);
  noLoop();
}

Funcția paint pentru desenarea fractalului ia ca parametri coordonatele pătratului negru curent (cx și cy), lungimea laturii sale împărțită la trei (len) și iterația curentă (it). Mai întâi, desenăm pătratul alb din centrul celui negru: rect(cx, cy, len, len). Apoi, apelăm recursiv funcția paint pentru cele opt pătrate ce se formează în jurul celui alb. Pentru aceste apeluri, parametrul len va fi len / 3, it va fi it + 1, iar coordonatele cx și cy se deduc ușor din imaginea următoare:

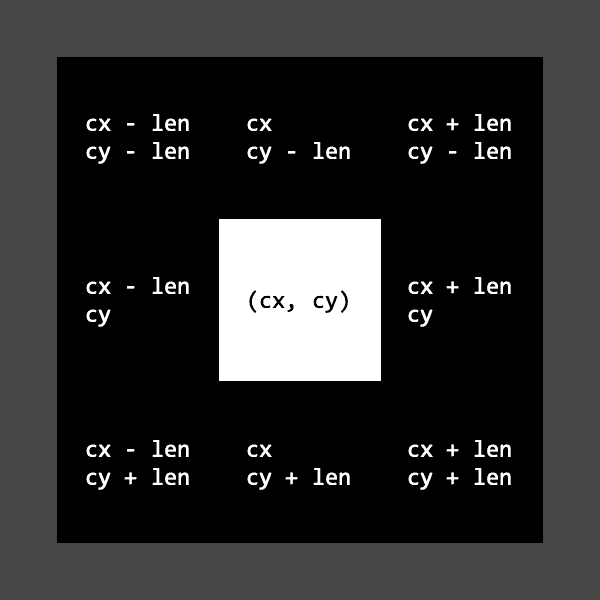
Așadar, iată rezultatul și scriptul final:

Covorul lui Sierpinski
function setup() {
  createCanvas(300, 300);
  rectMode(CENTER);
  noStroke();
}

function draw() {
  background(70);
  fill(0);
  rect(width / 2, height / 2, 243, 243);
  fill(255);
  paint(width / 2, height / 2, 81, 1);
  noLoop();
}

function paint(cx, cy, len, it) {
  if (it > MAX) return;
  rect(cx, cy, len, len);
  paint(cx - len, cy - len, len / 3, it + 1);
  paint(cx      , cy - len, len / 3, it + 1);
  paint(cx + len, cy - len, len / 3, it + 1);
  paint(cx - len, cy      , len / 3, it + 1);
  paint(cx + len, cy      , len / 3, it + 1);
  paint(cx - len, cy + len, len / 3, it + 1);
  paint(cx      , cy + len, len / 3, it + 1);
  paint(cx + len, cy + len, len / 3, it + 1);
}

let MAX = 0;
function mousePressed() {
  if (mouseX < width / 2 && MAX > 0) MAX--;
  if (mouseX > width / 2 && MAX < 5) MAX++;
  loop();
}

Buretele lui Menger

Sper că nu v-ați plictisit de fractalii lui Sierpinski, pentru că acum avem unul 3D: Buretele lui Menger. Se pornește de la un cub pe care îl împărțim în $27$ de cubulețe egale. Se elimină cuburile din centrul fiecărei fețe, precum și cel din centrul cubului mare, și se repetă procedeul pentru fiecare cubuleț pe care nu l-am eliminat.

Cuburi în P5.JS

Înainte de toate, trebuie să anunțăm faptul că lucrăm cu obiecte 3D, așa că o să apelăm funcția createCanvas puțin diferit: createCanvas(300, 300, WEBGL). Apoi, trebuie să vedem cum desenăm cuburi în P5.JS. Pentru asta, folosim funcția box, care poate primi mai mulți parametri, dar noi ne vom mulțumi cu unul singur: lungimea laturii cubului.

function setup() {
  createCanvas(300, 300, WEBGL);
  noStroke();
}

function draw() {
  background(30);
  fill(255);
  box(50);
}

Iată ce se întâmplă dacă rulăm codul de mai sus:

Funcțiile `rotateX` și `rotateY`

Avem mai multe probleme. În primul rând, din cauza unghiului din care ne uităm la cub, acesta nu prea arată a cub. Și chiar dacă am schimba unghiul, n-ar fi mare lucru, pentru că am vedea doar trei fețe ale cubului. O idee mai bună ar fi să rotim cubul (de fapt întreg sistemul de coordonate), ca să vedem pe rând fiecare față. Mă refer la efectul de mai jos. (Bine, dacă vă uitați atent, una dintre fețe nu apare în prim-plan niciodată. Dar nu contează, oricum avem o perspectivă mult mai bună.)

Pentru a roti sistemul de coordonate tridimensional, putem folosi funcțiile rotateX și rotateY în felul următor:

function draw() {
  ...
  rotateX(frameCount * 0.01);
  rotateY(frameCount * 0.01);
  ...
}

Acestea rotesc sistemul de coordonate în jurul axelor $OX$ și respectiv $OY$ cu unghiul specificat. Rotațiile efectuate se resetează la următorul apel al funcției draw. Unghiurile se măsoară în mod implicit în radiani; putem schimba asta, dar nu e nevoie. frameCount e o variabilă care ne indică numărul frame-ului curent. Practic, rotim obiectele cu un unghi care crește cu $0.01$ radiani la fiecare frame.

Funcțiile `lights` și `translate`

Uitându-ne la animația de mai sus, putem observa o nouă problemă. Cele trei fețe vizibile ale cubului au aceeași nuanță de alb. Cu alte cuvinte, lipsesc umbrele. Putem rezolva asta cu un apel la funcția lights în cadrul lui draw, înainte de a desena orice obiect. După cum îi zice și numele, funcția lights proiectează lumină asupra obiectelor noastre.

Mult mai bine. Dar încă avem o problemă. În caz că n-ați observat, atunci când apelăm funcția box, nu avem unde specifica coordonatele cubului. Soluția este să translăm sistemul de coordonate, folosind funcția translate(x, y, z). Aceasta mută toate obiectele ce urmează a fi desenate mai „încolo” cu x pixeli pe axa $OX$ cu y pe $OY$ și cu z pe $OZ$ Pentru a reveni la originea inițială după ce am desenat un obiect la poziția (x, y, z), trebuie să translăm din nou spațiul, dar „înapoi”, deci cu lungimi negative: translate(-x, -y, -z).

Funcția `paint`

Acum că știm cum să plasăm cuburi în spațiu, putem trece la desenarea efectivă a fractalului. Spre deosebire de Covorul lui Sierpinski, unde tot „ștergeam” din pătratul mare desenând pătrate albe peste el, aici nu putem porni de la un cub mare din care să tot ștergem cuburi mici. Odată ce am plasat o bucată de material într-un anumit punct, nu o mai putem scoate de acolo (în cadrul aceluiași frame).

Prin urmare, funcția paint trebuie gândită în așa fel încât cuburile mici să fie desenate abia atunci când ne oprim din recursie, pentru că atunci știm sigur că nu va mai trebui să eliminăm bucăți din ele. Din același motiv, dacă vrem să avem o iterație zero, cubul respectiv va trebui să fie desenat în funcția paint, nu în draw. Asta înseamnă că ne vom opri din recursie atunci când it devine egal cu MAX, nu când îl depășește.

Am ales ca lungimea laturii cubului să fie $3^3 \cdot 3 = 81$ Factorul $3^3$ vine de la numărul maxim de iterații, iar $3$ de la latura celor mai mici cuburi de la a treia iterație. Când ajungem la aceasta, cubul deja se mișcă foarte greu, iar dacă am mai adăuga una, probabil că vă va exploda calculatorul.

Parametrii funcției paint vor fi latura cubului curent împărțită la trei (len) și iterația curentă (it). Începutul funcției arată așa:

if (it === MAX) {
  box(len * 3);
  return;
}

Împărțirea cubului

Urmează să împărțim cubul curent în $27$ de cubulețe de latură len. Știind că în centrul sistemului de coordonate se află cubul mare, celelalte cuburi se vor afla la ±len pixeli de centru, pe fiecare axă. Ca să menținem această proprietate (faptul că în centrul sistemului de coordonate se află cubul curent) și pentru următoarele apeluri recursive, trebuie să translăm planul înainte și după fiecare dintre acestea, folosind mărimile corespunzătoare. Iată la ce mă refer:

for (let x = -len; x <= +len; x += len) {
  for (let y = -len; y <= +len; y += len) {
    for (let z = -len; z <= +len; z += len) {
      if (...) continue; // cazul în care „eliminăm” cubul de coordonate (x, y, z)
      translate(+x, +y, +z);
      paint(len / 3, it + 1);
      translate(-x, -y, -z);
    }
  }
}

Mai rămâne să completăm if-ul. Avem $20$ de cuburi pe care le păstrăm și $7$ pe care le eliminăm. $20$ este considerabil mai mare decât $7$ motiv pentru care este mai ușor să analizăm cuburile pe care le eliminăm. Dar și șapte cazuri sunt cam multe pentru un if. Observăm că, pentru fiecare cub din centrul unei fețe, două coordonate sunt zero, iar a treia e nenulă. Deja am redus șase cazuri la trei. Dacă punem și cubul din centrul cubului mare, obținem doar patru cazuri:

if (x === 0 && y === 0 && z === 0) continue;
if (x === 0 && y === 0 && z !== 0) continue;
if (x === 0 && y !== 0 && z === 0) continue;
if (x !== 0 && y === 0 && z === 0) continue;

Mai jos aveți rezultatul și scriptul final:

Buretele lui Menger
function setup() {
  createCanvas(300, 300, WEBGL);
  noStroke();
}

function draw() {
  background(30);
  rotateX(frameCount * 0.01);
  rotateY(frameCount * 0.01);
  lights();
  fill(255);
  paint(27, 0);
}

function paint(len, it) {
  if (it === MAX) {
    box(len * 3);
    return;
  }
  for (let x = -len; x <= +len; x += len) {
    for (let y = -len; y <= +len; y += len) {
      for (let z = -len; z <= +len; z += len) {
        if (x === 0 && y === 0 && z === 0) continue;
        if (x === 0 && y === 0 && z !== 0) continue;
        if (x === 0 && y !== 0 && z === 0) continue;
        if (x !== 0 && y === 0 && z === 0) continue;
        translate(+x, +y, +z);
        paint(len / 3, it + 1);
        translate(-x, -y, -z);
      }
    }
  }
}

let MAX = 0;
function mousePressed() {
  if (mouseX < width / 2 && MAX > 0) MAX--;
  if (mouseX > width / 2 && MAX < 3) MAX++;
  loop();
}

Fractalul lui Vicsek

Denumirea alternativă este Fulgul de zăpadă al lui Vicsek, dar mie nu prea mi se pare că arată a fulg de zăpadă. Mai degrabă se chema Crucea lui Vicsek. Se pornește de la un pătrat pe care îl împărțim în nouă pătrate egale. Eliminăm pătratele din colțuri și repetăm procedeul pentru cele rămase.

Funcția paint primește ca parametri coordonatele centrului pătratului curent (cx și cy), lungimea laturii sale împărțită la trei (len) și iterația curentă (it). Latura pătratului inițial este $2^5 = 243$ așa că primul apel al funcției paint va fi paint(width / 2, height / 2, 81, 0). La fel ca în cazul fractalului precedent, vom desena pătratele albe abia când ajungem pe ultimul nivel de recursie. Deci, primul lucru pe care îl facem în paint este să testăm dacă suntem la iterația MAX, caz în care desenăm un pătrat de latură 3 * len cu centrul în (cx, cy). Cred că nu mai e nevoie să intru în detalii cu împărțirea pătratului, semănând mult cu cea de la Covorul lui Sierpinski.

Rezultatul și scriptul final:

Fractalul lui Vicsek
function setup() {
  createCanvas(300, 300);
  rectMode(CENTER);
  noStroke();
}

function draw() {
  background(30);
  fill(255);
  paint(width / 2, height / 2, 81, 0);
  noLoop();
}

function paint(cx, cy, len, it) {
  if (it === MAX) {
    rect(cx, cy, len * 3, len * 3);
    return;
  }
  paint(cx      , cy - len, len / 3, it + 1);
  paint(cx - len, cy      , len / 3, it + 1);
  paint(cx      , cy      , len / 3, it + 1);
  paint(cx + len, cy      , len / 3, it + 1);
  paint(cx      , cy + len, len / 3, it + 1);
}

let MAX = 0;
function mousePressed() {
  if (mouseX < width / 2 && MAX > 0) MAX--;
  if (mouseX > width / 2 && MAX < 5) MAX++;
  loop();
}

Arbore binar

Arborii, atât cei din natură, cât și cei de la info, pot fi priviți drept fractali, așa că nu trebuie să poarte numele cuiva. Se pornește de la un trunchi din care se nasc două ramificații. În vârful fiecărei dintre ele apar alte două noi ramuri și tot așa.

Ca să obținem un arbore cum sunt cei din imagine, funcția paint va trebui să aibă șapte parametri: x și y (coordonatele vârfului ramurii curente), len (lungimea ramurii curente), color (nuanța de gri), weight (grosimea), angle (unghiul pe care îl va forma ramura curentă cu cele care ies din ea) și, evident, it (iterația curentă). La fiecare pas, len scade cu 20%, color scade cu 10%, weight scade cu o unitate, iar angle crește cu 10%.

Funcțiile `draw` și `setup`

Funcția draw arată așa:

function draw() {
  background(30);
  stroke(255);
  strokeWeight(11);
  line(250, 460, 250, 360);
  paint(250, 360, 80, 229.5, 10, 15, 1);
  noLoop();
}

Culoarea trunchiului este $255$ (alb), iar grosimea $11$ (pentru că în total vom avea maxim unsprezece iterații). Pentru desenarea sa, apelăm funcția line(x1, y1, x2, y2), care desenează un segment cu extremitățile în (x1, y1) și (x2, y2). Vârful trunchiului este $(250, 360)$ iar lungimea sa e $460 - 360 = 100$ În apelul inițial al lui paint am aplicat deja modificările descrise mai sus: $100 \cdot 0.8 = 80$ $255 \cdot 0.9 = 229.5$ și $11 - 1 = 10$ Unghiul inițial l-am setat la $15^{\circ}$

În funcția setup, setăm canvas-ul la $500 \times 500$ și schimbăm unitatea de măsură a unghiurilor din radiani în grade:

function setup() {
  createCanvas(500, 500);
  angleMode(DEGREES);
}

Funcția `paint`

Să vedem cum desenăm două ramuri pornind din vârful unei ramuri date. Ca să nu facem cine știe ce calcule complicate, ne vom folosi de funcțiile rotate și translate. Data trecută când am vorbit despre ele eram în spațiu; acum ne-am întors în plan: rotate(deg) rotește sistemul cartezian cu deg grade în sens antitrigonometric (sensul acelor de ceasornic), iar translate(x, y) îl translează cu x pixeli la dreapta și cu y în jos.

Mai întâi, translăm sistemul de coordonate în vârful ramurii curente, iar apoi îl rotim cu -angle grade. După acești doi pași, putem spune cu ușurință că vârful următoarei ramuri se află în punctul (0, -len).

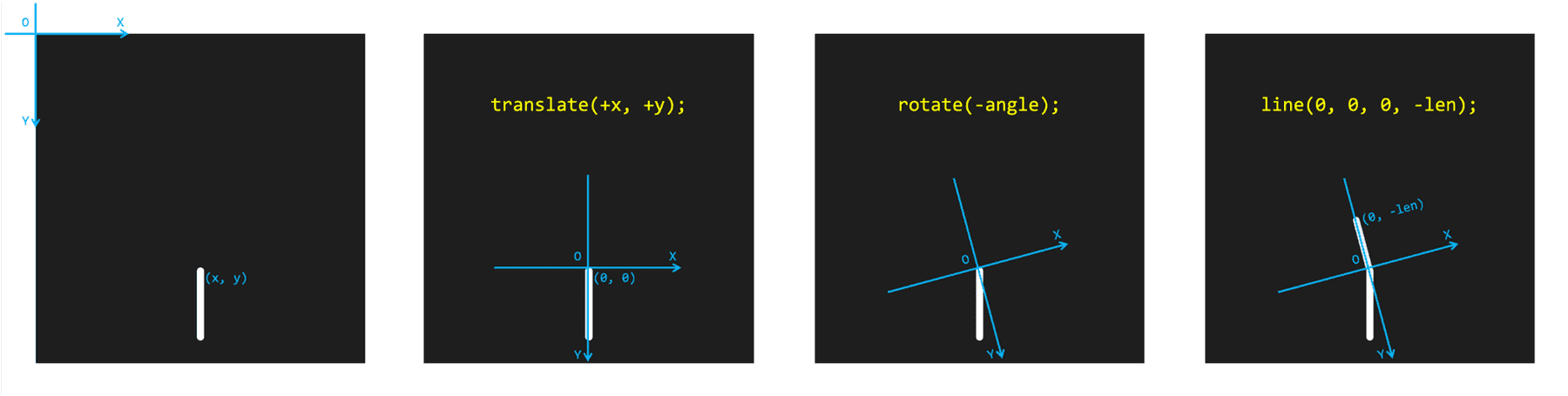
Codul este următorul:

translate(+x, +y);
rotate(-angle);
stroke(color);
strokeWeight(weight);
line(0, 0, 0, -len);
paint(0, -len, len * 0.8, color * 0.9, weight - 1, angle * 1.1, it + 1);

Pentru ramura din dreapta, ne rotim cu 2 * angle grade din poziția precedentă, desenăm ramura și continuăm recursia. La final, translăm planul la poziția dinaintea apelului curent, prin translate(-x, -y).

rotate(+2 * angle);
stroke(color);
strokeWeight(weight);
line(0, 0, 0, -len);
paint(0, -len, len * 0.8, color * 0.9, weight - 1, angle * 1.1, it + 1);
rotate(-angle);
translate(-x, -y);

Iată rezultatul și scriptul final:

Arbore binar
function setup() {
  createCanvas(500, 500);
  angleMode(DEGREES);
}

function draw() {
  background(30);
  stroke(255);
  strokeWeight(11);
  line(250, 460, 250, 360);
  paint(250, 360, 80, 229.5, 10, 15, 1);
  noLoop();
}

function paint(x, y, len, color, weight, angle, it) {
  if (it > MAX) return;
  translate(+x, +y);
  rotate(-angle);
  stroke(color);
  strokeWeight(weight);
  line(0, 0, 0, -len);
  paint(0, -len, len * 0.8, color * 0.9, weight - 1, angle * 1.1, it + 1);
  rotate(+2 * angle);
  stroke(color);
  strokeWeight(weight);
  line(0, 0, 0, -len);
  paint(0, -len, len * 0.8, color * 0.9, weight - 1, angle * 1.1, it + 1);
  rotate(-angle);
  translate(-x, -y);
}

let MAX = 0;
function mousePressed() {
  if (mouseX < width / 2 && MAX > 0) MAX--;
  if (mouseX > width / 2 && MAX < 10) MAX++;
  loop();
}

Fulgul de zăpadă al lui Koch

Pentru a desena Fulgul de zăpadă al lui Koch, se pornește de la un triunghi echilateral. Împărțim fiecare latură a sa în trei segmente egale și desenăm un triunghi echilateral cu baza în segmentul din mijloc. Repetăm procedeul pentru fiecare dintre cele patru segmente care se formează pe fiecare latură a triunghiului inițial, și continuăm așa cu fiecare nou segment.

Este interesant că perimetrul Fulgului de zăpadă tinde spre infinit pe măsură ce creștem iterațiile, spre deosebire de perimetrul Fractalului lui Vicsek, care este același indiferent de iterație. Asta în timp ce aria fractalului va fi mereu mărginită de aria cercului circumscris triunghiului inițial.

Funcția `draw`

Fulgul de zăpadă n-ar trebui să fie foarte greu de desenat, având în vedere că deja știm de la fractalii precedenți tot ce avem nevoie. La începutul lui draw desenăm un triunghi cu vârfurile în $(150, 45)$ $(28, 255)$ și $(271, 255)$ Funcția paint va primi ca parametri lungimea segmentului curent împărțită la trei (len) și iterația curentă (it).

Ideea de bază este că ne vom asigura ca atunci când apelăm funcția paint, segmentul curent să fie situat pe axa $OX$ și centrat în originea sistemului de coordonate. Deci, ca să terminăm funcția draw, luăm pe rând fiecare latură, translăm sistemul cartezian în mijlocul ei și îl rotim cu câte grade este nevoie. Unghiurile pot fi citite din următorea imagine:

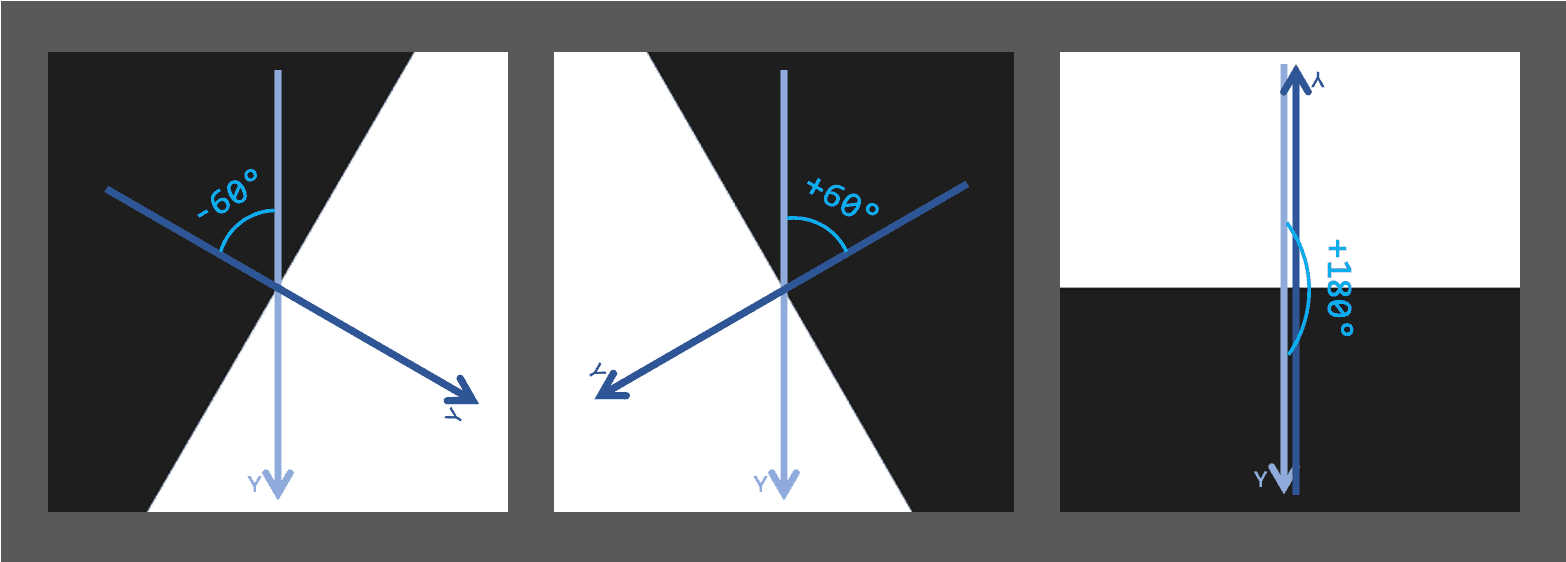
Iată codul:

function draw() {
  background(30);
  fill(255);
  triangle(150, 45, 28, 255, 271, 255);

  translate(+89, +150);
  rotate(-60);
  paint(81, 1);
  rotate(+60);
  translate(-89, -150);

  translate(+149.5, +255);
  rotate(+180);
  paint(81, 1);
  rotate(-180);
  translate(-149.5, -255);

  translate(+210.5, +150);
  rotate(+60);
  paint(81, 1);
  rotate(-60);
  translate(-210.5, -150);
  noLoop();
}

Funcția `paint`

În funcția paint trebuie să împărțim segmentul curent în trei bucăți egale și să desenăm triunghiul echilateral cu baza în cea din mijloc. Iată coordonatele triunghiului:

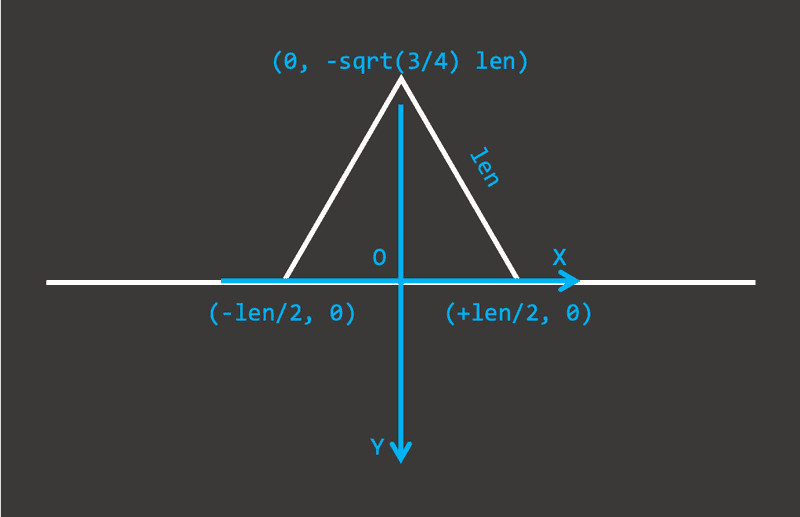
sqrt(3 / 4) * len este înălțimea triunghiului echilateral, care se obține ușor din Teorema lui Pitagora. Radicalul poate fi aproximat cu $0.86$ După ce desenăm triunghiul, ne mutăm pe rând în mijlocul fiecărui segment dintre cele patru noi, folosind funcțiile translate și rotate, și continuăm recursia:

triangle(0, -0.86 * len, -len / 2, 0, +len / 2, 0);

translate(-len, 0);
paint(len / 3, it + 1);
translate(+len, 0);

translate(-len / 4, -0.43 * len);
rotate(-60);
paint(len / 3, it + 1);
rotate(+60);
translate(+len / 4, +0.43 * len);

translate(+len / 4, -0.43 * len);
rotate(+60);
paint(len / 3, it + 1);
rotate(-60);
translate(-len / 4, +0.43 * len);

translate(+len, 0);
paint(len / 3, it + 1);
translate(-len, 0);

Iată animația și scriptul final:

Fulgul de zăpadă al lui Koch
function setup() {
  createCanvas(300, 370);
  angleMode(DEGREES);
  noStroke();
}

function draw() {
  background(30);
  fill(255);
  triangle(150, 45, 28, 255, 271, 255);

  translate(+89, +150);
  rotate(-60);
  paint(81, 1);
  rotate(+60);
  translate(-89, -150);

  translate(+149.5, +255);
  rotate(+180);
  paint(81, 1);
  rotate(-180);
  translate(-149.5, -255);

  translate(+210.5, +150);
  rotate(+60);
  paint(81, 1);
  rotate(-60);
  translate(-210.5, -150);
  noLoop();
}

function paint(len, it) {
  if (it > MAX) return;
  triangle(0, -0.86 * len, -len / 2, 0, +len / 2, 0);

  translate(-len, 0);
  paint(len / 3, it + 1);
  translate(+len, 0);

  translate(-len / 4, -0.43 * len);
  rotate(-60);
  paint(len / 3, it + 1);
  rotate(+60);
  translate(+len / 4, +0.43 * len);

  translate(+len / 4, -0.43 * len);
  rotate(+60);
  paint(len / 3, it + 1);
  rotate(-60);
  translate(-len / 4, +0.43 * len);

  translate(+len, 0);
  paint(len / 3, it + 1);
  translate(-len, 0);
}

let MAX = 0;
function mousePressed() {
  if (mouseX < width / 2 && MAX > 0) MAX--;
  if (mouseX > width / 2 && MAX < 5) MAX++;
  loop();
}

Mulțimea lui Mandelbrot

Mulțimea lui Mandelbrot este cu siguranță cel mai interesant fractal de pe lista asta. Se bazează pe o definiție matematică foarte complicată și aparent complet random, dar care conduce la un rezultat extraordinar. În plus, definiția nici nu se bazează pe recursivitate.

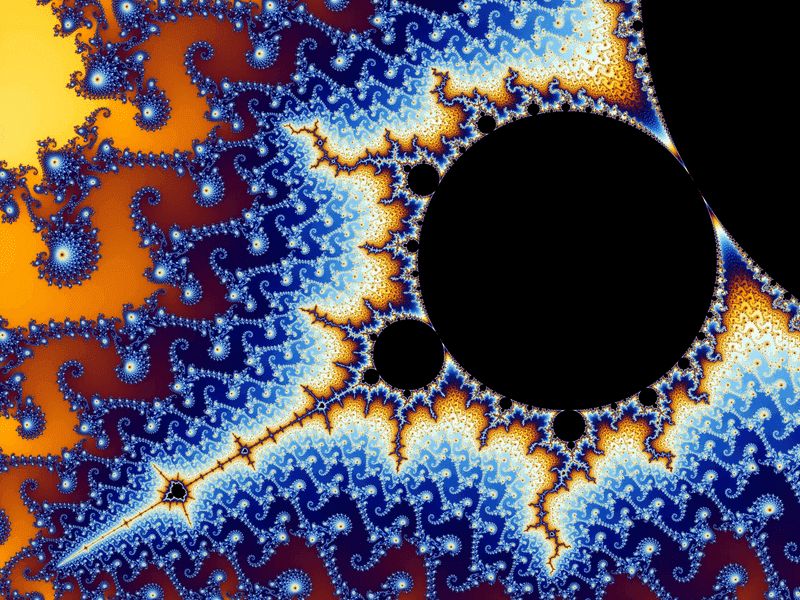
Mai întâi, să definim noțiunea de plan complex. Planul complex se referă la planul în care fiecărui punct (în cazul nostru pixel) de coordonate $(x, y)$ îi asociem numărul complex $x + yi$ Apoi, vom defini o familie de funcții complexe $f_c(z) = z^2 + c$ Pentru fiecare număr complex $c$ iterăm funcția $f_c(z)$ pornind de la $z = 0$ A itera o funcție înseamnă a aplica funcția pe ea însăși de mai multe ori. Iterațiile funcției $f_c(z)$ începând de la cea cu numărul zero, sunt:

z, f_c(z), f_c(f_c(z)), f_c(f_c(f_c(z))), \ldots

Dacă, iterând funcția asta, modulul ei tinde la infinit, atunci punctului $c$ îi asociem culoarea alb, iar în caz contrar negru. Vom vedea mai târziu cum putem folosi mai multe culori, dar deocamdată păstrăm definiția asta.

Lucrul cu pixeli în P5.JS

Înainte de toate, trebuie să vedem cum putem modifica culoarea unui anumit pixel din canvas în P5.JS. Primul pas este să setăm densitatea pixelilor la $1$ căci altfel lucrurile s-ar complica la maxim.

function setup() {
  createCanvas(500, 500);
  pixelDensity(1);
}

Ca să accesăm pixelii canvas-ului, trebuie să apelăm funcția loadPixels(), iar când îi terminăm de editat, apelăm updatePixels(). Pixelii sunt stocați într-un vector global numit pixels, obținut prin liniarizarea unui tablou tridimensional în care prima dimensiune reprezintă linia (paralelă cu axa $OX$ a doua coloana (paralelă cu axa $OY$ iar a treia se referă la componentele culorii din punctul respectiv: roșu, verde, albastru și alpha (opacitatea).

loadPixels();
for (let x = 0; x < width; x++) {
  for (let y = 0; y < height; y++) {
    const pixel = (x + y * width) * 4;
    // componentele pixelului (x, y):
    pixels[pixel + 0] = ...;
    pixels[pixel + 1] = ...;
    pixels[pixel + 2] = ...;
    pixels[pixel + 3] = 255;
  }
}
updatePixels();

Înainte să calculăm culoarea fiecărui pixel, ne vom fixa trei variabile globale:

let cx = 0, cy = 0;
let len = 5;

$cx$ și $cy$ reprezintă centrul regiunii din planul complex pe care o vedem în canvas, iar $len$ este jumătate din lungimea ei. Practic, asociem pixelii din canvas cu numere complexe de forma $a + bi$ unde $cx - len \le a \le cx + len$ și $cy - len \le b \le cy + len$

Funcția `map`

Putem calcula cărui număr complex îi corespunde fiecare pixel $(x, y)$ folosind regula de trei simplă, însă P5.JS ne pune la dispoziție o funcție foarte utilă care face asta pentru noi: map(x, a1, b1, a2, b2). Aceasta asociază (mapează) fiecare număr real cuprins între $a_1$ și $b_1$ cu fiecare număr real din intervalul $[a_2, b_2]$ returnând valoarea corespunzătoare lui $x \in [a_1, b_1]$ în $[a_2, b_2]$ (Nu prea contează cât de „închise” sunt intervalele respective.) Iată la ce mă refer prin maparea asta:

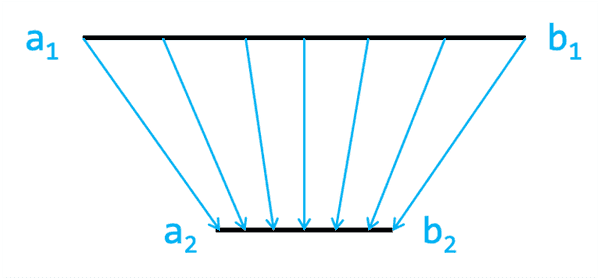
Așa calculăm deci numerele $a_0$ și $b_0$ componentele numărului complex $c$ corespunzător pixelului $(x, y)$

const a0 = map(x, 0, width, cx - len, cx + len);
const b0 = map(y, 0, height, cy - len, cy + len);

Simularea funcției $f_c(z)$

Acum urmează să verificăm dacă $|f_c(f_c(f_c({\cdots})))|$ tinde la infinit. Evident că nu putem calcula o infinitate de iterații ale funcției, așa că vom seta de la început un număr maxim de iterații (MAX = 100), precum și un infinit fictiv (INF = 10). Dacă, după MAX iterații, modulul funcției $f_c$ încă n-a atins valoarea INF, atunci vom considera că nu tinde la infinit.

let i = 0;
for (let a = 0, b = 0; i < MAX; i++) {
  const aNow = a * a - b * b + a0;
  const bNow = 2 * a * b + b0;
  a = aNow;
  b = bNow;
  if (a * a + b * b >= INF * INF) break;
}

În aNow și bNow calculăm componentele reală și respectiv imaginară ale funcției $f_c(a + bi)$

\begin{align*} f_c(z) &= z^2 + c\\ &= (a + bi)^2 + (a_0 + b_0 i)\\ &= a^2 + 2abi - b^2 + a_0 + b_0 i\\ &= (a^2 - b^2 + a_0) + (2ab + b_0) i \end{align*}

Pe liniile 5 și 6 transmitem aceste valori variabilelor $a$ și $b$ ce reprezentă următorul $z$ Apoi, testăm dacă $|z| \ge \mathrm{INF}$ adică dacă $a^2 + b^2 \ge \mathrm{INF}^2$ În caz afirmativ, dăm break. Mai rămâne să setăm culoarea pixelului și suntem gata:

const pixel = (x + y * width) * 4;
pixels[pixel + 0] = i === MAX ? 0 : 255;
pixels[pixel + 1] = i === MAX ? 0 : 255;
pixels[pixel + 2] = i === MAX ? 0 : 255;
pixels[pixel + 3] = 255;

Deocamdată, fractalul arată așa:

Un truc pentru a-l face mai interesant este să le asociem punctelor o nuanță de gri în funcție de cât de repede se apropie de infinit. Altfel spus, după câte iterații au atins infinitul. Nimic mai simplu; folosim funcția map:

const pixel = (x + y * width) * 4;
pixels[pixel + 0] = map(i, 0, MAX, 255, 0);
pixels[pixel + 1] = map(i, 0, MAX, 255, 0);
pixels[pixel + 2] = map(i, 0, MAX, 255, 0);
pixels[pixel + 3] = 255;

Colorarea pixelilor

Acum putem observa ceva mai mult detaliu, însă putem extinde ultima idee la mai multe culori, ceea ce chiar va merita la final, când o să dăm zoom la fractal. Vom încerca să copiem scara de culori din widget-ul Google menționat la începutul articolului:

Dacă vă uitați cu atenție la caseta RGB din stânga-jos, veți remarca faptul că scara de culori pornește de la $(255, 0, 0)$ și este compusă din șase „etape”:

Verdele crește de la $0$ la $255$
Roșul scade de la $255$ la $0$
Albastrul crește de la $0$ la $255$
Verdele scade de la $255$ la $0$
Roșul crește de la $0$ la $255$
Albastrul scade de la $255$ la $0$

Acum, setarea culorii unui pixel devine:

const pixel = (x + y * width) * 4;
if (i === MAX) {
  pixels[pixel + 0] = 0;
  pixels[pixel + 1] = 0;
  pixels[pixel + 2] = 0;
}
else {
  const rgb = getRGB(floor(map(i, 0, MAX, 0, 1535)));
  pixels[pixel + 0] = rgb[0];
  pixels[pixel + 1] = rgb[1];
  pixels[pixel + 2] = rgb[2];
}
pixels[pixel + 3] = 255;

Dacă modulul funcției nu tinde la infinit, setăm direct culoarea pixelului la negru. Dacă da, mapăm numărul de iterații necesare la una dintre cele $256 \cdot 6 = 1536$ de culori din scara descrisă mai sus. Funcția getRGB(x) returnează un vector de trei elemente cu valorile RGB ale culorii cu numărul x:

function getRGB(x) {
  if (floor(x / 256) === 0) return [255, x % 256, 0];
  if (floor(x / 256) === 1) return [255 - x % 256, 255, 0];
  if (floor(x / 256) === 2) return [0, 255, x % 256];
  if (floor(x / 256) === 3) return [0, 255 - x % 256, 255];
  if (floor(x / 256) === 4) return [x % 256, 0, 255];
  if (floor(x / 256) === 5) return [255, 0, 255 - x % 256];
}

Obținem:

Zoom

Acum putem trece la ultimul pas. Vrem să putem da zoom la fractal. Mai exact, când dăm click într-un anumit punct, animația trebuie să producă un zoom $2 \times$ către punctul respectiv. În acest sens, vom scrie o funcție mousePressed, care se apelează automat atunci când dăm click undeva. Aceasta mapează cx și cy la punctul corespunzător cursorului, împarte lungimea regiunii vizibile la doi și crește valorile MAX și INF cu 12.3%; m-am gândit că astfel vom menține un nivel de detaliu decent.

function mousePressed() {
  cx = map(mouseX, 0, width, cx - len, cx + len);
  cy = map(mouseY, 0, height, cy - len, cy + len);
  len /= 2;
  MAX = ceil(MAX * 1.123);
  INF *= 1.123;
  loop();
}

Pe lângă asta, am mai scris o funcție keyPressed care să ne întoarcă la starea inițială când apăsăm tasta backspace:

function keyPressed() {
  if (keyCode === BACKSPACE) {
    INF = 10;
    MAX = 100;
    cx = cy = 0;
    len = 5;
    loop();
  }
}

Și, ca un ultim detaliu, am setat în funcția setup pictograma cursorului la HAND, ca să ne sugereze faptul că scopul animației este să dăm zoom: cursor(HAND). Gata! Iată animația și scriptul final:

Mulțimea lui Mandelbrot
let INF = 10;
let MAX = 100;

function setup() {
  createCanvas(500, 500);
  pixelDensity(1);
  cursor(HAND);
}

let cx = 0, cy = 0;
let len = 5;

function draw() {
  loadPixels();
  for (let x = 0; x < width; x++) {
    for (let y = 0; y < height; y++) {
      const a0 = map(x, 0, width, cx - len, cx + len);
      const b0 = map(y, 0, height, cy - len, cy + len);

      let i = 0;
      for (let a = 0, b = 0; i < MAX; i++) {
        const aNow = a * a - b * b + a0;
        const bNow = 2 * a * b + b0;
        a = aNow;
        b = bNow;
        if (a * a + b * b >= INF * INF) break;
      }

      const pixel = (x + y * width) * 4;
      if (i === MAX) {
        pixels[pixel + 0] = 0;
        pixels[pixel + 1] = 0;
        pixels[pixel + 2] = 0;
      }
      else {
        const rgb = getRGB(floor(map(i, 0, MAX, 0, 1535)));
        pixels[pixel + 0] = rgb[0];
        pixels[pixel + 1] = rgb[1];
        pixels[pixel + 2] = rgb[2];
      }
      pixels[pixel + 3] = 255;
    }
  }
  updatePixels();
  noLoop();
}

function getRGB(x) {
  if (floor(x / 256) === 0) return [255, x % 256, 0];
  if (floor(x / 256) === 1) return [255 - x % 256, 255, 0];
  if (floor(x / 256) === 2) return [0, 255, x % 256];
  if (floor(x / 256) === 3) return [0, 255 - x % 256, 255];
  if (floor(x / 256) === 4) return [x % 256, 0, 255];
  if (floor(x / 256) === 5) return [255, 0, 255 - x % 256];
}

function mousePressed() {
  cx = map(mouseX, 0, width, cx - len, cx + len);
  cy = map(mouseY, 0, height, cy - len, cy + len);
  len /= 2;
  MAX = ceil(MAX * 1.123);
  INF *= 1.123;
  loop();
}

function keyPressed() {
  if (keyCode === BACKSPACE) {
    INF = 10;
    MAX = 100;
    cx = cy = 0;
    len = 5;
    loop();
  }
}

După vreo patruzeci de zoom-uri nu se va mai înțelege nimic, pentru că tipul de date standard pentru numere nu permite o precizie a zecimalelor chiar atât de mare. Dar, puteți vedea aici un zoom incredibil de detaliat, până la $10^{227} \times$ care a fost randat pe durata a patru săptămâni. Totuși, dacă știți în ce puncte să dați zoom, puteți surprinde imagini interesante și cu aplicația noastră :smile:

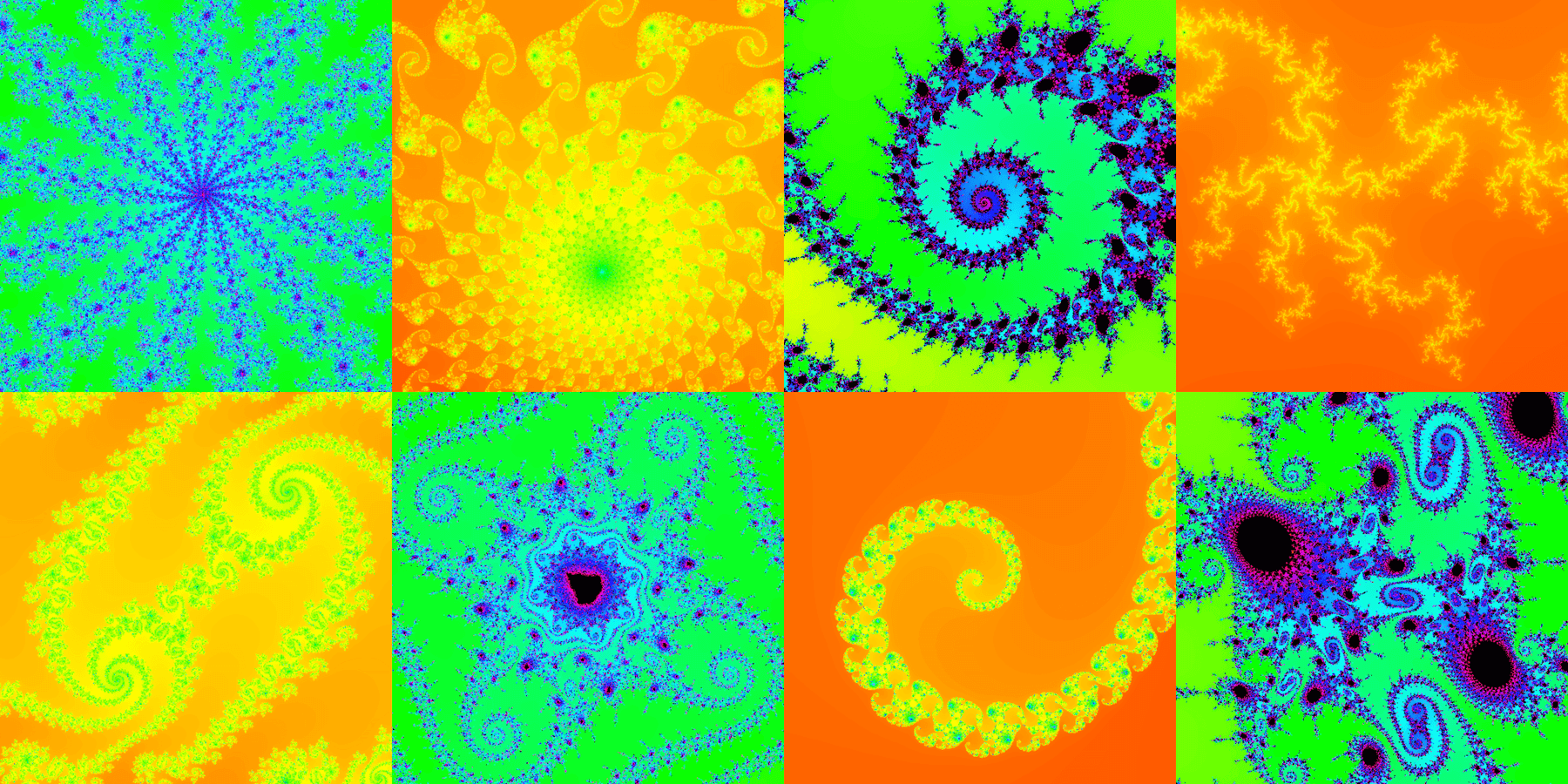
Cam atât despre fractali. Sper că vi s-a părut și vouă un subiect interesant și că veți crea și voi la rândul vostru animații sau chiar jocuri folosind JavaScript și P5.JS! Dacă aveți întrebări sau sugestii pentru articolele următoare, nu ezitați să le lăsați mai jos, în rubrica de comentarii.

PS: Wow, 5693 de cuvinte! Cred că merită un share articolul ăsta :yey:

Desenarea fractalilor în P5.JS. Top 7 fractali!

Cuprins

Introducere în P5.JS

Prima animație

Observații

Triunghiul lui Sierpinski

Variabila `MAX` și funcția `keyPressed`

Funcțiile `setup` și `draw`

Funcția `paint`

Covorul lui Sierpinski

Pătrate în P5.JS

Funcțiile `draw` și `paint`

Buretele lui Menger

Cuburi în P5.JS

Funcțiile `rotateX` și `rotateY`

Funcțiile `lights` și `translate`

Funcția `paint`

Împărțirea cubului

Fractalul lui Vicsek

Arbore binar

Funcțiile `draw` și `setup`

Funcția `paint`

Fulgul de zăpadă al lui Koch

Funcția `draw`

Funcția `paint`

Mulțimea lui Mandelbrot

Lucrul cu pixeli în P5.JS

Funcția `map`

Simularea funcției $f_c(z)$

Colorarea pixelilor

Zoom

Lasă un comentariu!

0 comentarii