Descompunerea în factori primi. Probleme de divizibilitate în C++

În articolul precedent am prezentat Algoritmul lui Euclid și am rezolvat în C++ câteva probleme legate de CMMDC și CMMMC. Astăzi vom discuta despre descompunerea unui număr în factori primi și vom rezolva niște probleme clasice de divizibilitate, majoritatea legate de factorizarea întregilor.

Problema 1.

Se dă un număr natural nenul $n$ Să se afișeze toți divizorii numărului $n$

Cea mai simplă idee este să luăm pe rând fiecare număr natural $d$ de la $1$ la $n$ și să vedem dacă $n$ este divizibil cu acesta, adică dacă restul împărțirii lui $n$ la $d$ este $0$

for (int d = 1; d <= n; d++)
    if (n % d == 0)
        cout << d << ' ';
cout << '\n';

Totuși, această soluție este ineficientă. De exemplu, pentru $n = 10^9$ execuția programului durează două-trei secunde. Observația ce ne permite să optimizăm algoritmul este că, de fiecare dată când găsim un divizor $d$ al lui $n$ putem afirma că și $n / d$ este un divizor al lui $n$ Astfel, dacă la fiecare nou divizor îl afișăm atât pe el, cât și pe complementul lui, putem să ne oprim atunci când $d$ devine mai mare decât $n / d$

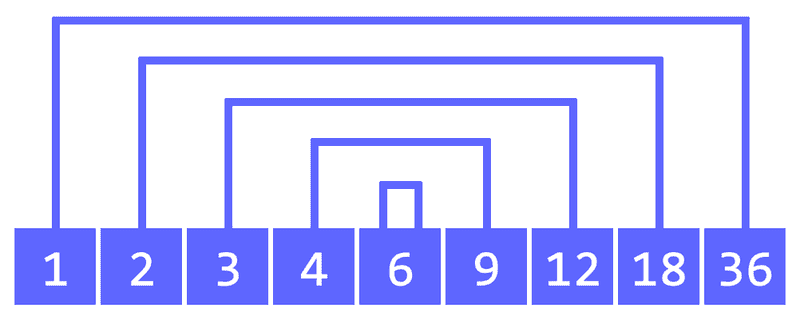
Ei bine, valoarea la care ne putem opri din a căuta divizori este $\sqrt{n}$ Dacă îl împărțim pe $n$ la un număr mai mic decât $\sqrt{n}$ sigur obținem un număr mai mare decât $\sqrt{n}$ La fel și invers.

Noul algoritm are complexitatea $O(\sqrt{n})$ care este mult mai bună decât precedentul $O(n)$ Pentru $n = 10^9$ se vor efectua doar $31\,622$ de pași, în loc de un miliard. Iată așadar codul:

for (int d = 1; d * d <= n; d++)
    if (n % d == 0) {
        cout << d << ' ';
        if (n / d != d)
            cout << n / d << ' ';
    }
cout << '\n';

Iar în caz că vrem să afișăm divizorii în ordine crescătoare, putem ca pe cei mai mici sau egali cu $\sqrt{n}$ să-i reținem într-un vector $l$ de lungime $p$ iar pe cei mai mari decât $\sqrt{n}$ într-un vector $r$ de lungime $q$ La final, afișăm elementele lui $l$ în ordine crescătoare, iar pe cele ale lui $r$ în ordine descrescătoare.

for (int d = 1; d * d <= n; d++)
    if (n % d == 0) {
        l[p++] = d;
        if (n / d != d)
            r[q++] = n / d;
    }
for (int i = 0; i < p; i++)
    cout << l[i] << ' ';
for (int i = q - 1; i >= 0; i--)
    cout << r[i] << ' ';
cout << '\n';

Problema 2. [Testul de primalitate]

Se dă un număr natural nenul $n$ Să se verifice dacă $n$ este un număr prim sau nu.

Mai întâi niște teorie. Divizorii $1$ și $n$ se numesc divizorii improprii ai lui $n$ pe când ceilalți divizori se numesc divizorii proprii. Un număr natural mai mare decât $1$ se numește prim dacă nu are niciun divizor propriu. Adică dacă are exact doi divizori (pozitivi). Adică dacă singurul său divizor diferit de $1$ este el însuși. Un număr natural mai mare decât $1$ se numește compus dacă nu este prim. Adică dacă poate fi scris drept produsul a mai multe numere prime (nu neapărat distincte). Numerele $0$ și $1$ nu sunt considerate nici prime, nici compuse.

Revenind la problema noastră, prima metodă de a verifica primalitatea unui număr este să-i numărăm toți divizorii și să testăm dacă numărul acestora este exact $2$

int cnt = 0;
for (int d = 1; d <= n; d++)
    if (n % d == 0)
        cnt++;
cout << (cnt == 2 ? "DA\n" : "NU\n");

Putem optimiza puțin codul căutând doar divizori proprii și dând break când l-am găsit pe primul. Însă, dacă procedăm așa, va trebui să tratăm separat cazul $n = 1$

bool ok = n > 1;
for (int d = 2; d < n; d++)
    if (n % d == 0) {
        ok = false;
        break;
    }
cout << (ok ? "DA\n" : "NU\n");

În continuare, putem reduce timpul de execuție la $O(\sqrt{n})$ aplicând observația de la problema precedentă. Știm că dacă nu am găsit niciun divizor până la $\sqrt{n}$ sigur nu vom găsi nici după. Dacă am găsi, acesta ar trebui să aibă un complement mai mic sau egal cu $\sqrt{n}$

bool ok = n > 1;
for (int d = 2; d * d <= n; d++)
    if (n % d == 0) {
        ok = false;
        break;
    }
cout << (ok ? "DA\n" : "NO\n");

Problema 3. [Descompunerea în factori primi]

Se dă un număr natural nenul $n$ Să se afișeze descompunerea sa în factori primi.

Descompunerea în factori primi (numită și factorizare) a unui număr natural nenul se referă la scrierea lui sub forma $p_1^{e_1} p_2^{e_2} \cdots p_k^{e_k}$ unde numerele $p_i$ sunt numere prime distincte. Algoritmul clasic presupune să luăm pe rând câte un număr prim $d$ și să testăm dacă $n$ este divizibil cu $d$ Dacă da, îl împărțim pe $n$ la $d$ cât timp $d \mid n$ calculând pe parcurs exponentul $e$ la care apare $d$ în descompunerea lui $n$ Ne oprim când $n = 1$

for (int d = 2; n > 1; d++)
    if (n % d == 0) {
        int e = 0;
        while (n % d == 0) {
            e++;
            n /= d;
        }
        cout << d << ' ' << e << '\n';
    }

Poate ați observat că în if n-am mai testat dacă $d$ este prim. Asta pentru că $d$ nici nu poate fi compus, căci $n$ a fost deja împărțit la toți divizorii primi ai lui $d$ așa că $d$ nu mai poate divide valoarea actuală a lui $n$

În ceea ce privește complexitatea, algoritmul nu e grozav. Dacă $n$ este prim, $d$ va trebui să ajungă la valoarea $n$ ca să putem ieși din for. Și ăsta nu e singurul caz în care algoritmul rulează în timp liniar. Un alt caz nefavorabil este cel în care $n$ este produsul dintre un număr prim foarte mic și unul foarte mare. De exemplu, $n = 2 \cdot 666\,013$ Algoritmul va efectua $666\,013$ pași, adică $O(n / 2)$ care e echivalent cu $O(n)$

Pentru a reduce complexitatea worst-case la $O(\sqrt{n})$ trebuie să ne oprim atunci când $d$ depășește radicalul lui $n$ Atunci vom ști sigur că ce a mai rămas din $n$ este un număr prim, pe care îl vom putea afișa când ieșim din for.

for (int d = 2; d * d <= n; d++)
    if (n % d == 0) {
        int e = 0;
        while (n % d == 0) {
            e++;
            n /= d;
        }
        cout << d << ' ' << e << '\n';
    }
if (n > 1)
    cout << n << " 1\n";

Problema 4.

Se dau două numere naturale nenule $a$ și $b$ Să se calculeze cel mai mare divizor comun al lor.

Deja am văzut în articolul despre Algoritmul lui Euclid cum putem calcula CMMDC-ul în timp logaritmic. Însă acum vreau să vă arăt soluția ce folosește descompunerea numerelor în factori primi, care evident că are complexitatea $O(\sqrt{n})$ bătând $O(n)$ul de la Algoritmul lui Euclid prin scăderi repetate.

Soluția constă în a calcula descompunerile numerelor $a$ și $b$ reținând în vectorii $div_a$ și $exp_a$ fiecare factor prim al lui $a$ și respectiv exponentul acestuia, și procedând similar cu $div_b$ și $exp_b$ După aceea, intersectăm cele două perechi de vectori folosind interclasare. Pentru fiecare divizor comun $d$ găsit, înmulțim răspunsul cu $d^{\min(exp_a, exp_b)}$

for (int d = 2; d * d <= a; d++)
    if (a % d == 0) {
        divA[x] = d;
        while (a % d == 0) {
            expA[x]++;
            a /= d;
        }
        x++;
    }
if (a > 1) {
    divA[x] = a;
    expA[x++] = 1;
}

for (int d = 2; d * d <= b; d++)
    if (b % d == 0) {
        divB[y] = d;
        while (b % d == 0) {
            expB[y]++;
            b /= d;
        }
        y++;
    }
if (b > 1) {
    divB[y] = b;
    expB[y++] = 1;
}

int gcd = 1;
divA[x] = divB[y] = 1e9;
for (int i = 0, j = 0; i < x || j < y; )
    if (divA[i] < divB[j])
        i++;
    else if (divA[i] > divB[j])
        j++;
    else {
        for (int k = 0; k < min(expA[i], expB[j]); k++)
            gcd *= divA[i];
        i++; j++;
    }
cout << gcd << '\n';

Problema 5.

Se dau două numere naturale nenule $a$ și $b$ Să se verifice dacă descompunerile numerelor $a$ și $b$ conțin aceeași factori primi.

Descompunem în factori primi numerele $a$ și $b$ urmând să verificăm dacă factorii primi găsiți în fiecare descompunere sunt aceiași. Am putea să reținem factorii primi ai fiecărui număr într-un vector, dar mai simplu este să calculăm produsul lor, la final rămânându-ne să verificăm doar dacă cele două produse sunt egale.

int descA = 1;
for (int d = 2; d * d <= a; d++)
    if (a % d == 0) {
        descA *= d;
        while (a % d == 0)
            a /= d;
    }
if (a > 1)
    descA *= a;

int descB = 1;
for (int d = 2; d * d <= b; d++)
    if (b % d == 0) {
        descB *= d;
        while (b % d == 0)
            b /= d;
    }
if (b > 1)
    descB *= b;
cout << (descA == descB ? "DA\n" : "NU\n");

Problema 6.

Se dă un număr natural nenul $n$ Să se verifice dacă $n$ este un număr aproape prim. Un număr se numește aproape prim dacă poate fi scris sub forma unui produs de două numere prime distincte.

Parcurgem numerele naturale de la $2$ la $\sqrt{n}$ (exclusiv). Dacă $n$ e divizibil cu $d$ și atât $d$ cât și $n / d$ sunt prime, atunci afișăm "DA" și ne oprim. Am definit o funcție isPrime(int n) care testează dacă $n$ este prim; era cam enervant să testăm primalitatea a două numere într-un for fără să folosim funcții.

#include <bits/stdc++.h>
using namespace std;

bool isPrime(int n) {
    for (int d = 2; d * d <= n; d++)
        if (n % d == 0)
            return false;
    return true;
}

int main() {
    int n; cin >> n;
    for (int d = 2; d * d < n; d++)
        if (n % d == 0 && isPrime(d) && isPrime(n / d)) {
            cout << "DA\n";
            return 0;
        }
    cout << "NU\n";
    return 0;
}

Complexitatea acestei soluții este $O(\sqrt{n} \cdot \sqrt{\sqrt{n}}) = O(n^{3/4}) = O(n^{0.75})$ Primul radical vine de la for, al doilea de la testul de primalitate, iar radicalul din interiorul celui din urmă vine de la faptul că numărul maxim pentru care se testează primalitatea este $\sqrt{n}$

Totuși, există și o soluție în $O(\sqrt{n})$ care se bazează pe ideea de la problema precedentă. Putem să-l descompunem în factori primi pe $n$ și să calculăm pe parcurs numărul factorilor primi găsiți, precum și produsul acestora. Dacă numărul lor e $2$ și produsul este egal cu $n$ atunci $n$ este aproape prim.

int cnt = 0, prod = 1;
for (int d = 2; d * d <= n; d++)
    if (n % d == 0) {
        cnt++;
        prod *= d;
        while (n % d == 0)
            n /= d;
    }
if (n > 1) {
    cnt++;
    prod *= n;
}
cout << (cnt == 2 && prod == n ? "DA\n" : "NU\n");

Problema 7.

Se dau două numere naturale nenule $a$ și $b$ Să se afișeze divizorii comuni ai acestora.

Dacă un număr $d$ îl divide atât pe $a$ cât și pe $b$ atunci trebuie să-l dividă pe $\gcd(a, b)$ Deci, mai întâi calculăm CMMDC-ul numerelor $a$ și $b$ iar apoi afișăm divizorii acestuia.

while (b) {
    int r = a % b;
    a = b;
    b = r;
}
for (int d = 1; d * d <= a; d++)
    if (a % d == 0) {
        cout << d << ' ';
        if (a / d != d)
            cout << a / d << ' ';
    }
cout << '\n';

Problema 8.

Se dă un număr natural nenul $n$ Să se determine câte perechi ordonate de numere naturale nenule $(a, b)$ există, cu proprietatea că $\lcm(a, b) = n$

Să scriem descompunerile în factori primi ale celor trei numere:

Pentru ca $\lcm(a, b)$ să fie egal cu $n$ trebuie ca:

Fiecare pereche de exponenți $(x_i, y_i)$ poate lua $2z_i + 1$ valori, și anume:

Prin urmare, răspunsul problemei este $(2z_1 + 1)(2z_2 + 1) \cdots (2z_k + 1)$ Putem calcula această expresie în timp ce descompunem numărul $n$ în factori primi.

int ans = 1;
for (int d = 2; d * d <= n; d++) {
    int e = 0;
    while (n % d == 0) {
        e++;
        n /= d;
    }
    ans *= 2 * e + 1;
}
cout << ans << '\n';

Problema 9.

Se dă un număr natural $n$ Să se determine în câte zerouri se termină numărul $n! = 1 \cdot 2 \cdots n$

Numărul de zerouri de la finalul unui număr $n$ este egal cu puterea maximă a lui $10$ cu care $n$ este divizibil (de fapt exponentul ei). Cum $10 = 2 \cdot 5$ valoarea căutată este dată de $\min(e_2(n), e_5(n))$ unde $e_d(n)$ este exponentul la care apare factorul $d$ în descompunerea lui $n$ Așadar, putem lua fiecare număr natural $i$ de la $1$ la $n$ și să calculăm valorile $e_2(i)$ și $e_5(i)$ pe care să le adunăm apoi la $e_2(n!)$ și $e_5(n!)$ La final, afișăm $\min(e_2(n!), e_5(n!))$

int e2 = 0, e5 = 0;
for (int i = 1; i <= n; i++) {
    int x = i;
    while (x % 2 == 0) {
        e2++;
        x /= 2;
    }
    while (x % 5 == 0) {
        e5++;
        x /= 5;
    }
}
cout << min(e2, e5) << '\n';

Dacă ne uităm mai atent, vom observa că nu este nevoie să calculăm și $e_2(n!)$ și $e_5(n!)$ pentru că $e_5(n!)$ va fi întotdeauna mai mic decât $e_2(n!)$ Acum că am făcut observația asta, putem parcurge numerele din $5$ în $5$ pentru că avem nevoie doar de multiplii lui $5$

int ans = 0;
for (int i = 5; i <= n; i += 5) {
    int x = i;
    while (x % 5 == 0) {
        ans++;
        x /= 5;
    }
}
cout << ans << '\n';

Până acum avem complexitatea $O(n)$ însă putem deduce o formulă ce ne va permite să calculăm răspunsul în timp logaritmic. Ideea este similară cu cea de la Ciurul lui Eratostene: La primul pas parcurgem din $5$ în $5$ numerele mai mici sau egale cu $n$ incrementând de fiecare dată rezultatul. Însă, în cazul multiplilor de $25$ am procesat un singur factor de $5$ din descompunerea lor, și știm că mai avem cel puțin unul. Deci, la al doilea pas parcurgem numerele din $25$ în $25$ incrementând de fiecare dată rezultatul. Apoi parcurgem numerele din $125$ în $125$ și tot așa.

În loc să parcurgem efectiv numerele din $5^i$ în $5^i$ adunând câte un $1$ la rezultat, putem să adunăm din start valoarea $[n / 5^i]$ pentru că acesta e numărul multiplilor lui $5^i$ mai mici sau egali cu $n$ Așadar, formula finală este:

Numărul de pași efectuați este $[\log_5 n]$ pentru că cea mai mare putere a lui $5$ mai mică sau egală cu $n$ este $5^{[\log_5 n]}$ Din acest motiv, complexitatea algoritmului este $O(\log n)$

int ans = 0;
for (int p = 5; p <= n; p *= 5)
    ans += n / p;
cout << ans << '\n';

Această formulă este un caz particular al formulei lui Legendre, care ne spune că exponentul lui $p$ din descompunerea în factori primi a lui $n!$ este:

Problema 10.

Se dă un număr natural $n$ Să se determine ultima cifră nenulă a numărului $n!$

Extragem din fiecare număr natural de la $1$ la $n$ toți factorii de $2$ și de $5$ posibili, calculând exponenții lor în $e_2$ și $e_5$ Între timp, calculăm modulo $10$ produsul dintre numerele rămase după extragerea factorilor respectivi. Apoi, înmulțim rezultatul cu $2^{e_2 - e_5}$ pentru că asta e puterea lui $2$ din $n!$ care nu contribuie la formarea de zerouri la finalul numărului. Evident că și această operație va fi efectuată modulo $10$

int e2 = 0, e5 = 0, ans = 1;
for (int i = 1; i <= n; i++) {
    int x = i;
    while (x % 2 == 0) {
        e2++;
        x /= 2;
    }
    while (x % 5 == 0) {
        e5++;
        x /= 5;
    }
    ans = ans * x % 10;
}
for (int i = 0; i < e2 - e5; i++)
    ans = ans * 2 % 10;
cout << ans << '\n';

Cam astea sunt cele mai importante probleme legate de descompunerea în factori primi. Puteți rezolva în continuare probleme de divizibilitate pe PbInfo. Urmează în curând un articol cu trei aplicații ceva mai avansate ale descompunerii în factori primi: Numărul divizorilor, suma divizorilor și indicatorul lui Euler. Dacă aveți vreo problemă de divizibilitate care vă dă bătăi de cap, nu ezitați o să lăsați mai jos, într-un comentariu, pentru a vă ajuta