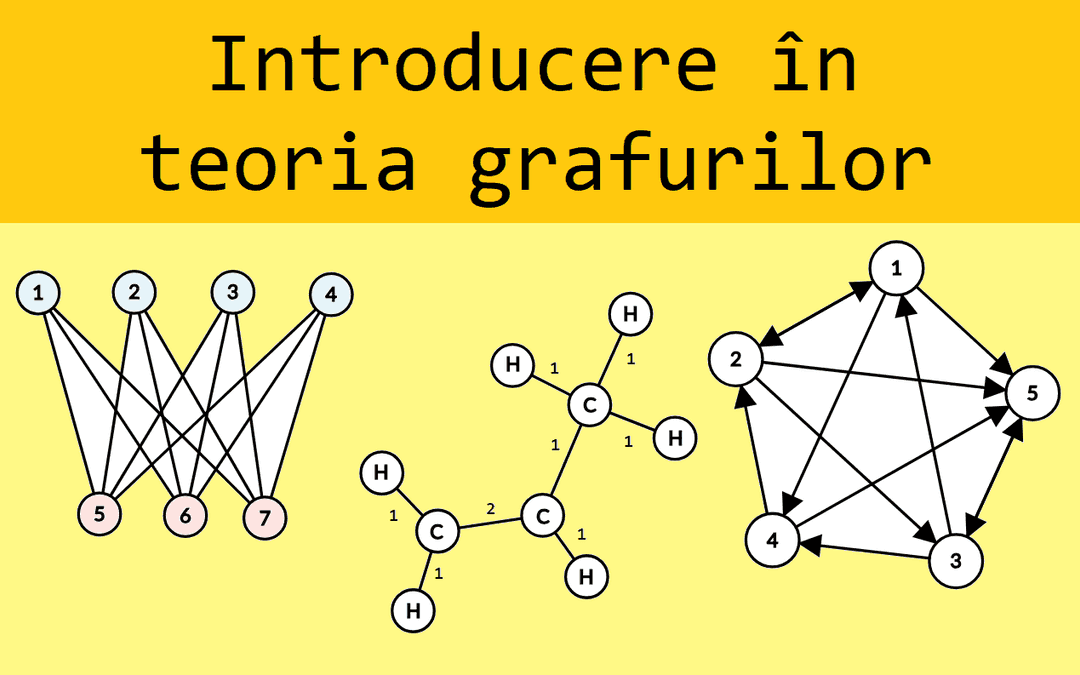
Introducere în teoria grafurilor – Noțiuni elementare despre grafuri

de Iulian Oleniuc | 05/05/2018 | Algoritmică și structuri de date, Teoria grafurilor

Matematic, un graf este o pereche ordonată de mulțimi, $G = (V, E)$ unde $V$ reprezintă o mulțime finită și nevidă de elemente numite vârfuri (sau noduri), iar $E$ este o mulțime de perechi cu elemente din $V$ numite muchii (dacă sunt neordonate) sau arce (dacă sunt ordonate). În primul caz graful se numește neorientat, iar în al doilea orientat (sau digraf).

Exemple de grafuri din viața de zi cu zi

Practic, un graf este un mod de a reprezenta elementele unei mulțimi și conexiunile dintre acestea, stabilite pe baza unei anumite relații. Graful este neorientat dacă relația respectivă este reflexivă, sau orientat în caz contrar. Iată câteva exemple:

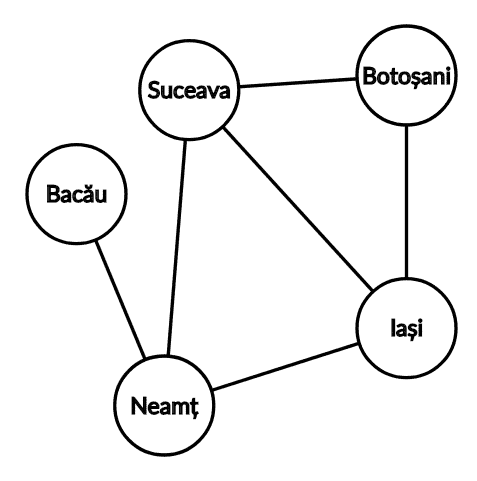
1. Harta unui oraș

Nodurile sunt intersecții, iar o muchie dintre două noduri reprezintă faptul că există o stradă între cele două intersecții. În cazul în care vrem să evidențiem faptul că unele străzi au sens unic, graful devine orientat. Astfel, dacă există muchie de la $A$ la $B$ înseamnă că din $A$ se poate ajunge în $B$ prin acel drum, dar nu și reciproc.

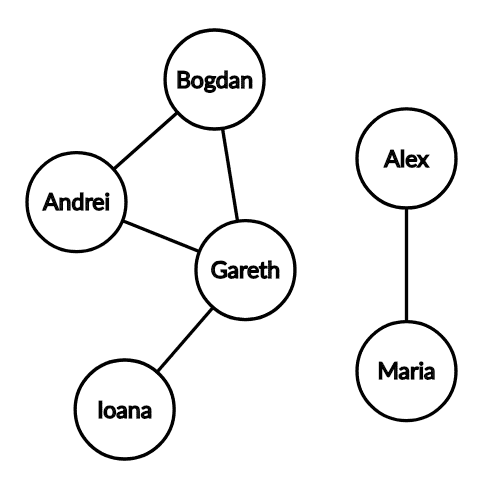
2. O rețea de socializare

Nodurile sunt utilizatorii, iar o muchie reprezintă relația de prietenie între doi utilizatori. Cum prietenia este o relație reflexivă, dacă $A$ este prieten cu $B$ înseamnă că și $B$ este prieten cu $A$ Așadar, vorbim despre un graf neorientat.

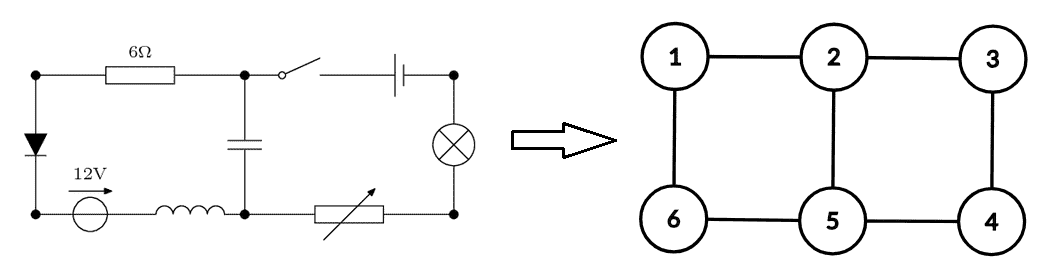
3. Un circuit electric

Făcând abstracție de elementele de circuit de pe laturile schemei (cum ar fi rezistorii), aceasta este un graf în care vârfurile sunt nodurile rețelei, iar ciclurile elementare sunt ochiurile acesteia. Fizicianul Kirchhoff a studiat rețelele electrice folosind metode care aparțin astăzi teoriei grafurilor, contribuind la dezvoltarea acesteia.

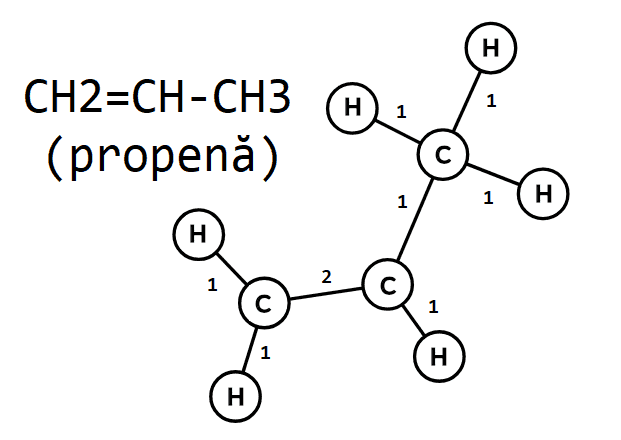
4. Formula de structură a unei substanțe chimice

Nodurile vor fi atomii (sau grupările de atomi), iar muchiile legăturile dintre aceștia. Eventual, costul fiecărei muchii poate reține tipul legăturii chimice dintre extremitățile ei.

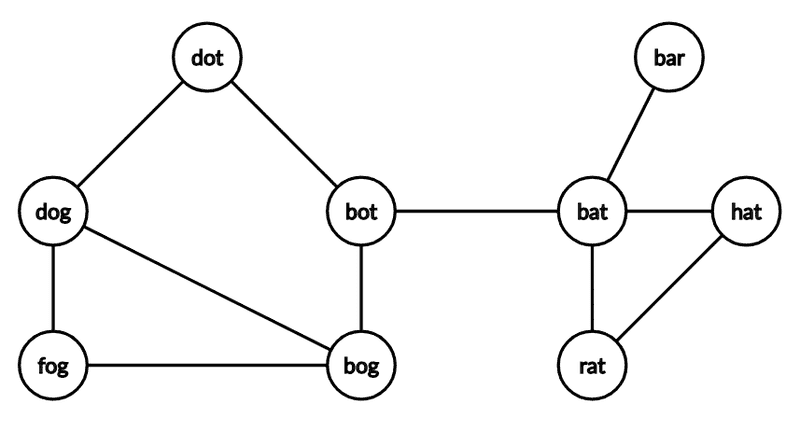
5. Un joc de cuvinte

Acesta e un exemplu mult mai abstract și interesant, găsit pe CSAcademy. Să presupunem că pornim de la un cuvânt de trei litere, căruia îi putem schimba succesiv câte o literă astfel încât să obținem un nou cuvânt valid. Scopul este de a ajunge la un cuvânt dat printr-un număr minim de pași. De exemplu (nu prea am găsit cuvinte în română):

\texttt{dog} \to \texttt{bog} \to \texttt{bot} \to \texttt{bat}

Putem modela un graf neorientat în care fiecare nod reține câte un cuvânt valid de trei litere. O muchie reprezintă faptul că se poate ajunge de la o extremitate la cealaltă printr-un singur pas. Pentru a rezolva problema va mai trebui doar să determinăm drumul minim de la nodul cu primul cuvânt la cel cu al doilea.

Grafurile se regăsesc des în viața de zi cu zi. De aceea, este important studiul algoritmilor specifici acestora, cum ar fi cei de găsire a drumului de lungime minimă (între două localități să zicem) și cel de determinare a fluxului maxim de cost minim (într-o rețea de țevi).

Noțiuni elementare din teoria grafurilor

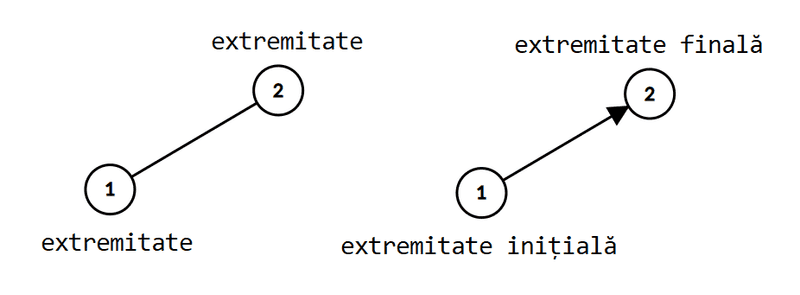
Cele două noduri $x$ și $y$ ce formează muchia $[x, y]$ se numesc extremități. În cazul grafurilor orientate, pentru arcul $(x, y)$ $x$ se numește extremitate inițială, iar $y$ extremitate finală. În plus, vom spune că $x$ și $y$ sunt noduri adiacente, și incidente la muchia/ arcul pe care îl formează.

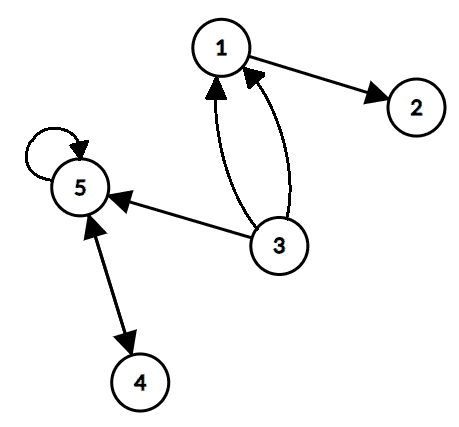
Într-un graf neorientat, nodurile cu gradul $0$ se numesc noduri izolate, iar cele cu gradul $1$ se numesc noduri terminale.

Graf simplu, multigraf

Între oricare două noduri ale unui graf simplu poate exista cel mult o muchie/ arc. În caz contrar, structura de date se va numi multigraf. Într-un multigraf, muchiile cu aceeași pereche de extremități se numesc muchii paralele. În plus, muchiile cu extremități identice (de la un nod la el însuși), se numesc bucle.

Aici apare o discuție, deoarece unii autori de specialitate consideră că doar multigrafurile (nu și grafurile) pot avea bucle, pe când ceilalți susțin contrariul. Preferabilă este prima variantă, pentru că altfel multe formule clasice legate de grafuri s-ar complica. De obicei se specifică în enunțul problemelor dacă graful poate avea bucle sau nu. Oricum, noi vom lucra doar cu grafuri simple.

Numărul maxim de muchii/ arce

Numărul maxim de muchii ale unui graf neorientat cu $n$ noduri este $n(n-1)/2$ pentru că, având la dispoziție $n$ noduri, se pot forma $C^2_n = n(n - 1) / 2$ perechi neordonate, iar în cel mai fericit caz, pentru oricare două noduri $x$ și $y$ din $V$ există muchia $[x, y]$ Similar, numărul maxim de arce ale unui graf orientat cu $n$ noduri este $2C^2_n = n(n - 1)$ pentru că două noduri $x$ și $y$ pot contribui cu maxim două arce: $(x, y)$ și $(y, x)$

Numărul de grafuri orientate/ neorientate

De aici mai putem deduce două formule: Numărul de grafuri neorientate cu $n$ noduri este $2^{n(n - 1) / 2}$ pentru că între fiecare două noduri pot exista $0$ sau $1$ muchii. Analog, numărul de grafuri orientate cu $n$ noduri este $4^{n(n - 1) / 2}$ pentru că între fiecare două noduri $x$ și $y$ pot exista arcul $(x, y)$ arcul $(y, x)$ ambele sau niciunul.

Gradul unui nod

Într-un graf neorientat, gradul unui nod reprezintă numărul de muchii incidente cu acesta, și se notează cu $d(x)$ Într-un graf orientat, gradul interior al nodului $x$ se notează cu $d^{-}(x)$ și este egal cu numărul de arce cu extremitatea finală $x$ iar gradul exterior, notat cu $d^{+}(x)$ este numărul arcelor cu extremitatea inițială $x$

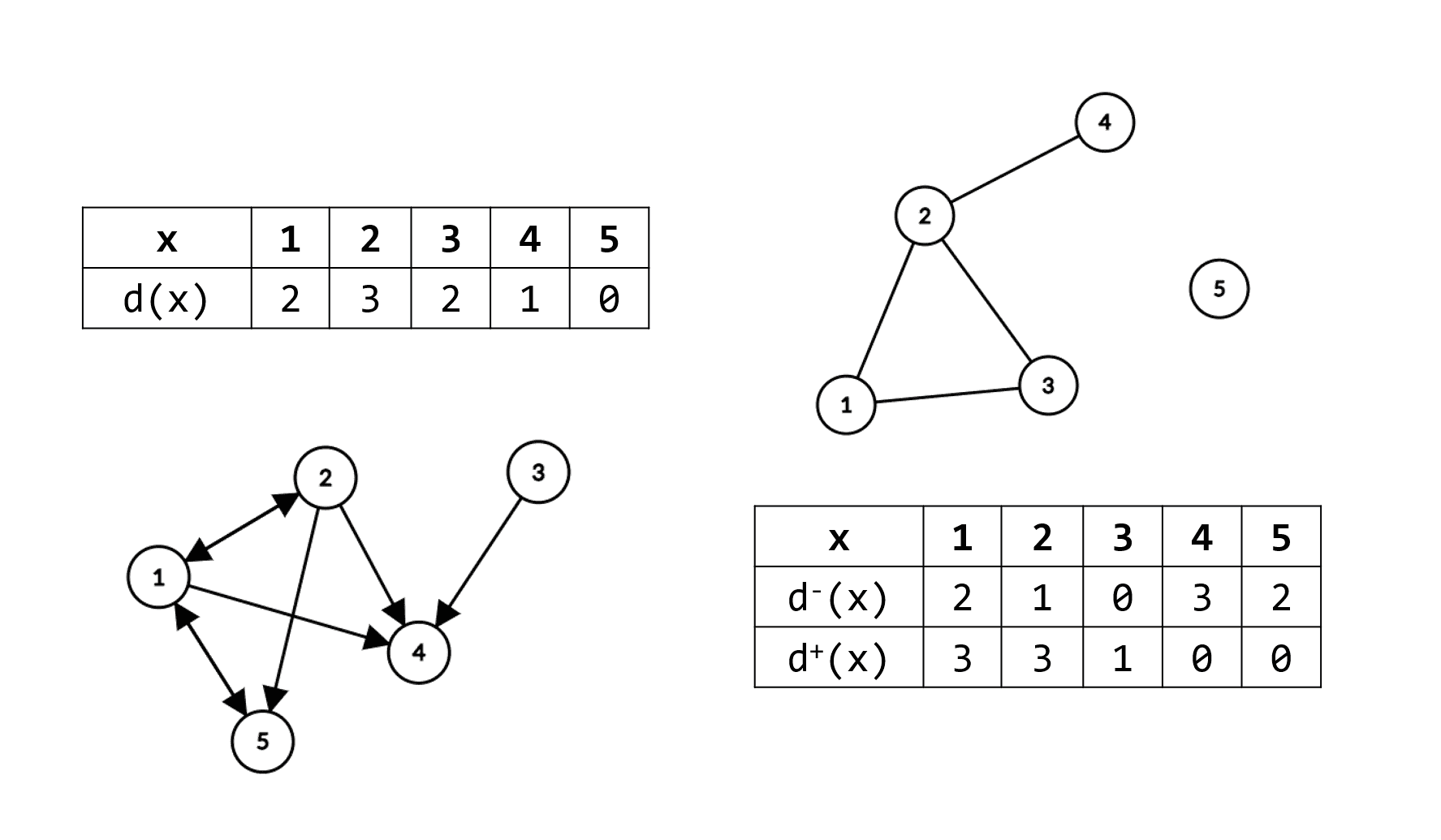
Suma gradelor nodurilor unui graf neorientat este egală cu dublul numărului său de muchii, pentru că fiecare muchie contribuie cu câte o unitate la gradul a două noduri:

\sum_{x \in V} d(x) = 2|E|

Atât suma gradelor interioare cât și suma gradelor exterioare ale nodurilor unui graf orientat sunt egale cu numărul de arce ale grafului, pentru că fiecare muchie contribuie cu câte o unitate la fiecare sumă:

\sum_{x \in V} d^{-}(x) = \sum_{x \in V} d^{+}(x) = |E|

Grafuri asociate unui graf

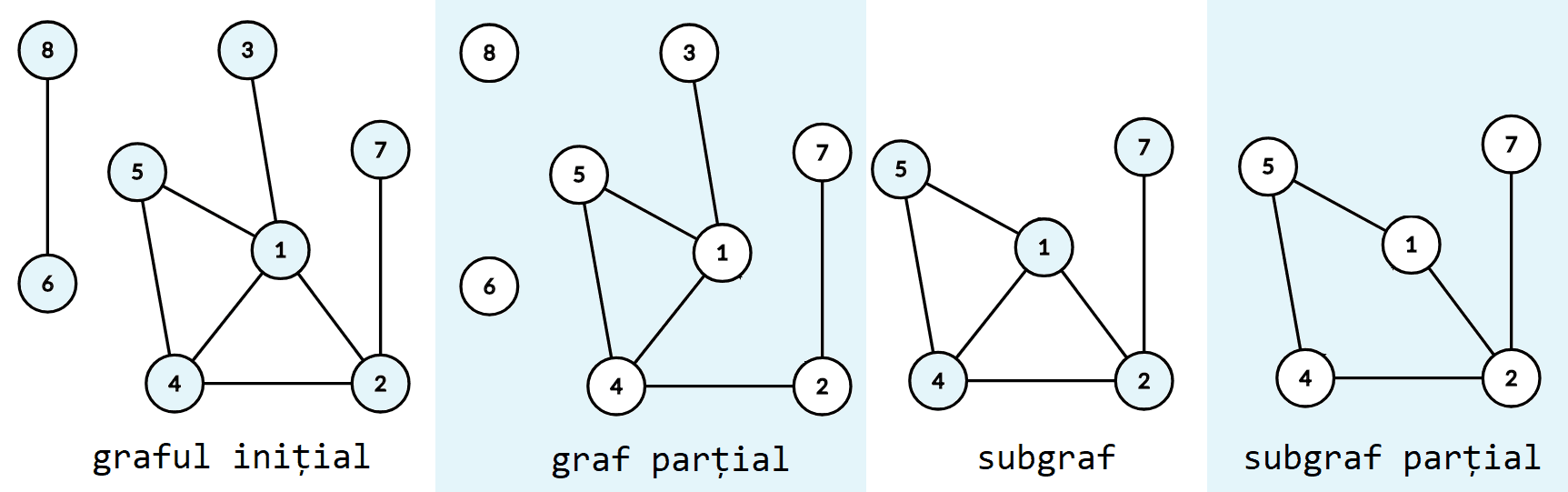
Fie graful $G = (V, E)$ Graful $G' = (V, E')$ cu $E' \subseteq E$ este un graf parțial al grafului $G$ Se observă că acesta se poate obține prin eliminarea unor muchii/ arce din graful inițial. Numărul grafurilor parțiale ale lui $G$ este $2^{|E|}$ (pentru fiecare muchie avem două variante: o ștergem sau nu).

Graful $G^{\prime\prime} = (V^{\prime\prime}, E^{\prime\prime})$ cu $V^{\prime\prime} \subseteq V$ și $E^{\prime\prime}$ mulțimea tuturor muchiilor/ arcelor din $E$ cu ambele extremități în $V^{\prime\prime}$ se numește subgraf al lui $G$ Acesta poate fi obținut eliminând unele noduri din $G$ împreună cu toate muchiile incidente la acestea. Numărul de subgrafuri ale lui $G$ este $2^{|V|} - 1$ (numărul submulțimilor lui $V$ excluzând mulțimea vidă, deoarece graful nu poate avea $0$ noduri).

Un subgraf parțial este, după cum îi spune și numele, un subgraf din care s-au eliminat niște muchii.

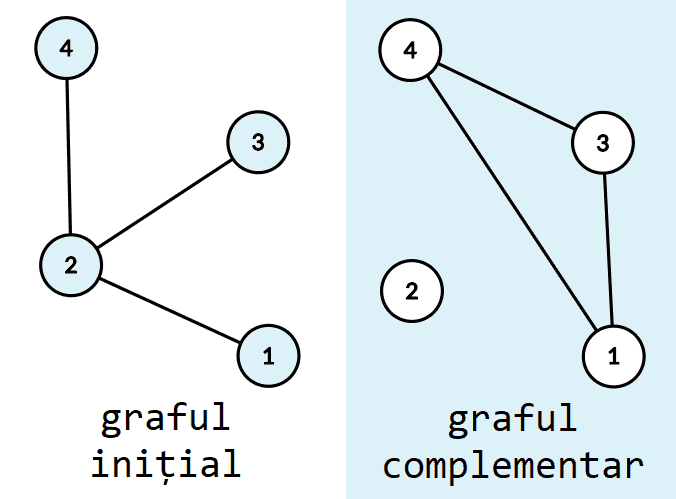
Graful complementar unui graf neorientat $G$ are aceeași mulțime de vârfuri, dar mulțimea muchiilor conține doar muchiile care nu apar în $G$

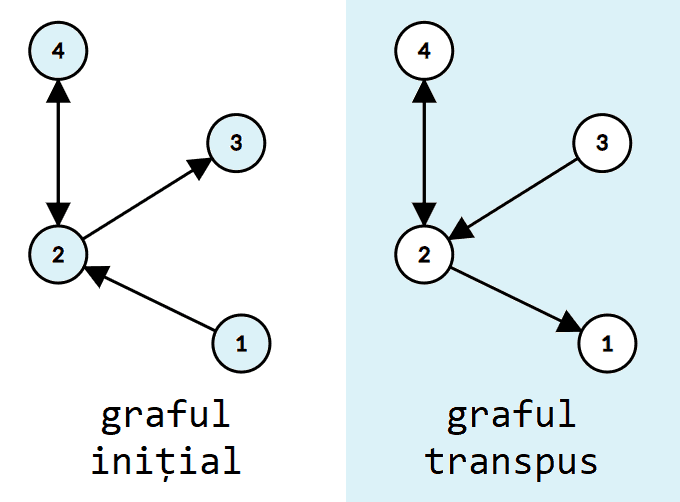
Pentru un graf orientat $G$ graful $G^T = (V, E^T)$ se numește graful transpus al lui $G$ dacă $E^T = \{(y, x) \mid (x, y) \in E\}$

Tipuri speciale de grafuri

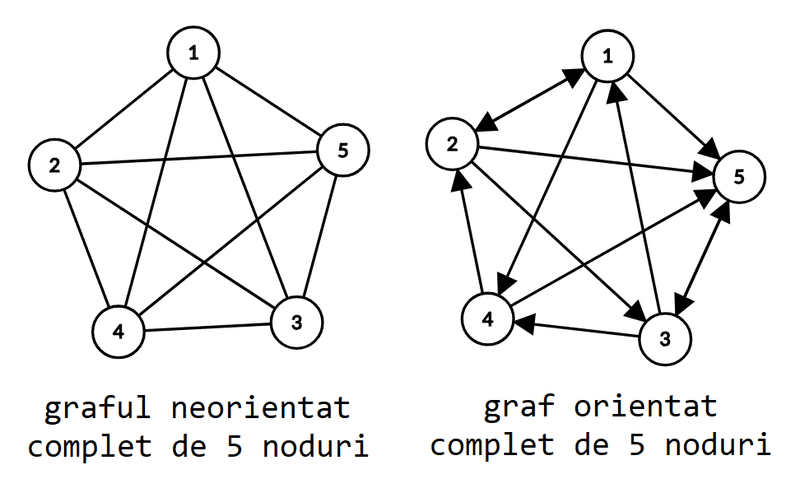
Un graf se numește complet dacă oricare două noduri ale sale sunt adiacente. Graful neorientat complet cu $n$ noduri se notează $K_n$ și conține $n(n - 1) / 2$ muchii.

Există un singur graf neorientat complet cu $n$ noduri, însă grafurile orientate complete cu $n$ noduri sunt mai multe. Mai exact, între oricare două noduri $x$ și $y$ pot exista ori arcul $(x, y)$ ori $(y, x)$ ori ambele. Deci, numărul grafurilor orientate complete cu $n$ noduri este $3^{n(n - 1) / 2}$

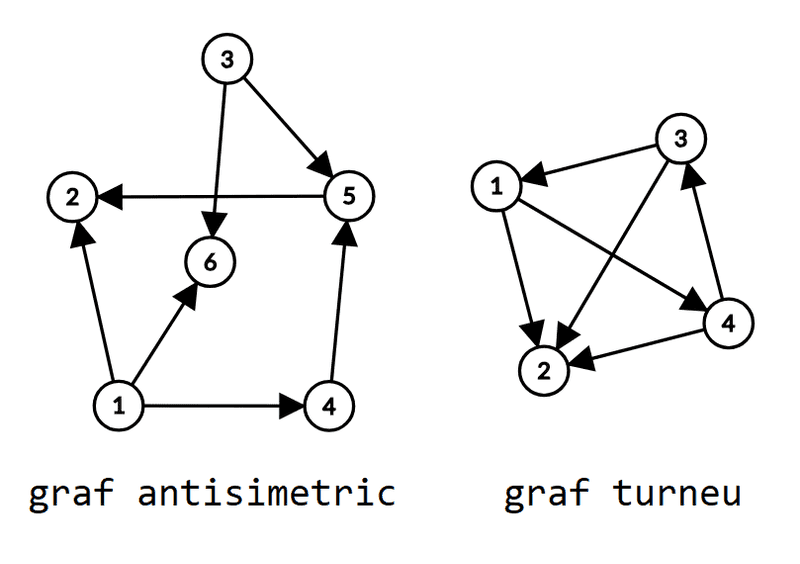
Un graf orientat se numește antisimetric în cazul în care pentru oricare două noduri $x$ și $y$ dacă există arcul $(x, y)$ atunci nu există și arcul $(y, x)$ Cu alte cuvinte, între două noduri există cel mult un arc. Există $3^{n(n - 1) / 2}$ grafuri antisimetrice, deoarece între două noduri $x$ și $y$ pot exista arcul $(x, y)$ arcul $(y, x)$ sau niciunul.

Un graf orientat complet și antisimetric se numește graf turneu. Numărul de grafuri turneu cu $n$ noduri este $2^{n(n - 1) / 2}$ căci între două noduri $x$ și $y$ poate exista arcul $(x, y)$ sau arcul $(y, x)$

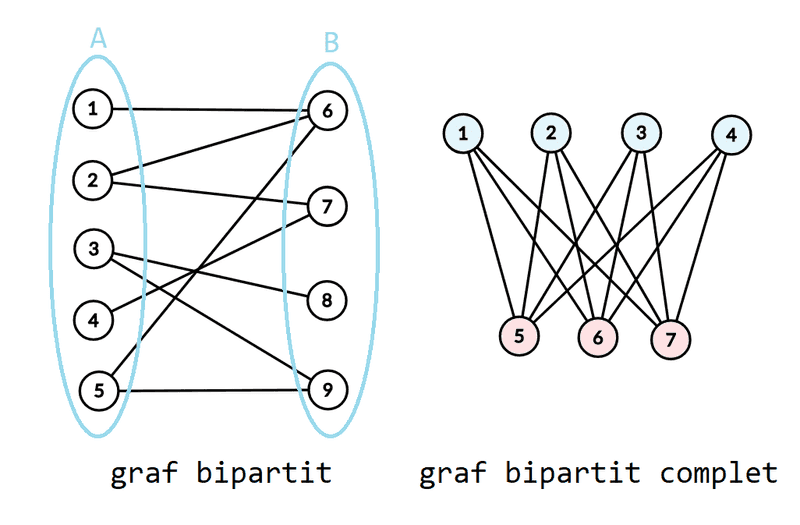
Un graf neorientat se numește bipartit dacă mulțimea muchiilor sale poate fi partiționată în două submulțimi $A$ și $B$ astfel încât orice muchie are o extremitate în $A$ și una în $B$ Un graf bipartit complet este un graf bipartit în care fiecare nod din $A$ este adiacent cu fiecare nod din $B$

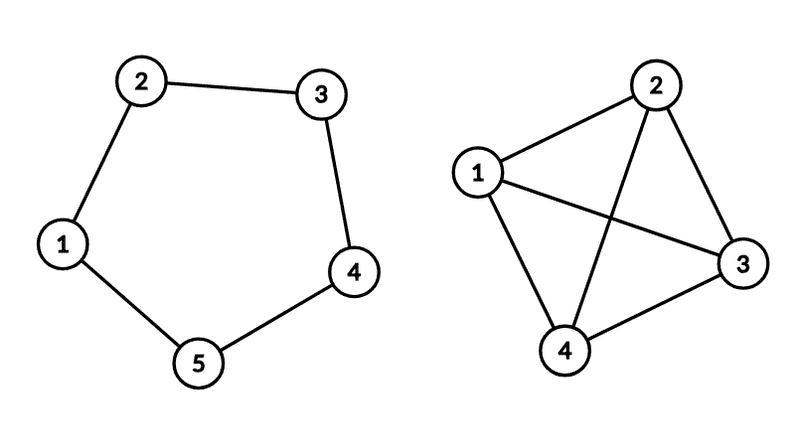
Un graf neorientat se numește regulat dacă toate nodurile sale au același grad.

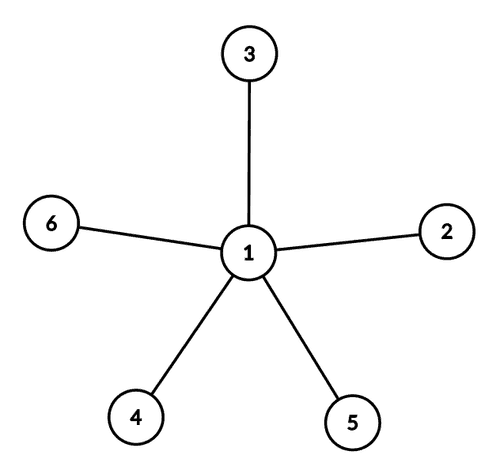
Un graf stea (star graph) este un graf neorientat format dintr-un nod la care s-au unit mai multe noduri terminale. Graful stea cu $n$ noduri terminale se notează cu $S_n$ De exemplu, așa arată $S_5$

Lanț, ciclu, drum, circuit

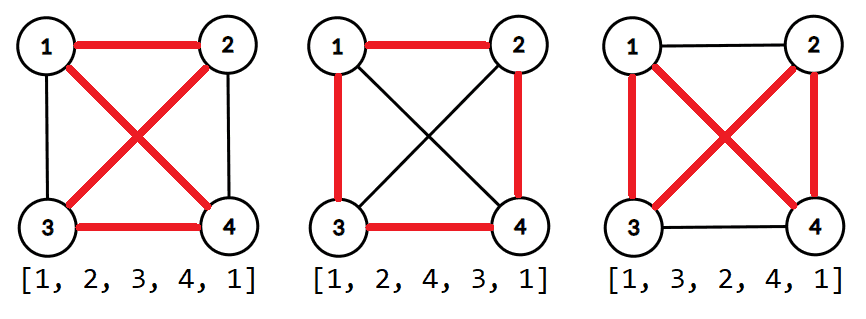
Într-un graf neorientat, un lanț este o secvență de noduri $[x_1, x_2, \ldots, x_k]$ cu proprietatea că oricare două noduri consecutive din secvență sunt adiacente. Extremitatea inițială a lanțului este $x_1$ iar cea finală $x_k$ Lungimea unui lanț este numărul muchiilor din care este compus, deci $k - 1$

Un lanț este elementar dacă nu conține de mai multe ori același nod. Un lanț se numește simplu dacă nu conține de mai multe ori aceeași muchie. Se observă că orice lanț elementar este automat și simplu. Un ciclu este un lanț simplu pentru care extremitatea inițială este aceeași cu cea finală. Ciclul este elementar dacă nu conține de mai multe ori același nod (cu excepția extremităților).

Similar sunt definite și drumurile (pentru grafurile orientate): Un drum este o secvență de noduri $(x_1, x_2, \ldots, x_k)$ cu proprietatea că pentru oricare două noduri consecutive $x_i$ și $x_{i+1}$ există arcul $(x_i, x_{i+1})$ În plus, ciclul se va numi de fapt circuit.

Un lanț/ drum/ ciclu/ circuit se numește hamiltonian dacă trece prin fiecare nod al grafului exact o singură dată. Un lanț/ drum/ ciclu/ circuit se numește eulerian dacă trece prin fiecare dintre muchiile/ arcele grafului exact o singură dată.

Numărul ciclurilor hamiltoniene dintr-un graf neorientat complet

Numărul de cicluri hamiltoniene din $K_n$ este egal cu $(n-1)!/2$ Cum ajungem la acest rezultat? Mai întâi fixăm primul nod al ciclului în $1$ căci vorbind de un ciclu, nu contează de unde începem. De exemplu, ciclul $[1, 2, 4, 3, 1]$ este tot una cu $[3, 1, 2, 4, 3]$ Rămân de permutat restul de $n - 1$ noduri ale grafului, de unde rezultă acel $(n - 1)!$ La final, împărțim rezultatul la $2$ pentru a nu număra același ciclu de două ori: o dată scris de la stânga la dreapta și o dată de la dreapta la stânga.

Conexitate

Un graf neorientat $G$ se numește conex dacă există lanț între oricare două noduri ale sale. O componentă conexă a lui $G$ este un subgraf conex maximal al său.

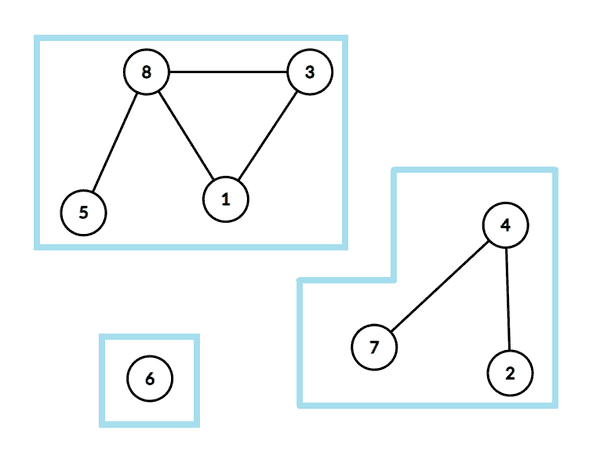
Un graf orientat $G$ se numește tare-conex dacă pentru oricare două noduri $x$ și $y$ ale sale există atât drum de la $x$ la $y$ cât și drum de la $y$ la $x$ O componentă tare-conexă a lui $G$ este un subgraf tare-conex maximal al său.

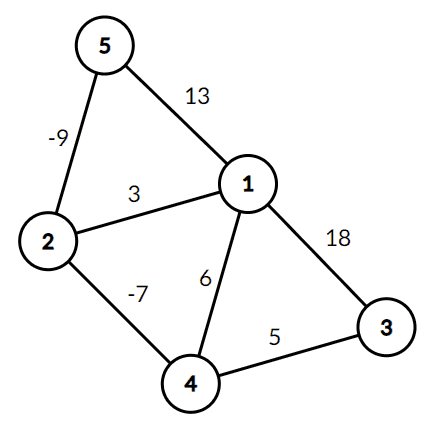
Grafuri ponderate

Adesea, modelarea problemelor practice necesită utilizarea unor grafuri în care muchiilor/ arcelor li se asociază costuri (ponderi). Astfel de grafuri se numesc grafuri ponderate. Funcția care asociază câte un cost fiecărei muchii/ arc a grafului se numește funcție de cost. De exemplu, avem un graf $G = (V, E)$ ce reprezintă harta unei țări, și funcția $f : V \to \mathbb{N}^{*}$ unde $f([x, y])$ reprezintă lungimea străzii dintre orașele $x$ și $y$

Note

Mulțimea vârfurilor unui graf poate conține orice fel de elemente, dar pentru simplitate am ales $V = \{1, 2, \ldots, |V|\}$
O partiție a unei mulțimi reprezintă un set de submulțimi ale sale, nevide și disjuncte, pentru care reuniunea lor este egală cu mulțimea respectivă.
Perechile neordonate se notează folosind paranteze pătrate, pe când perechile ordonate se notează folosind paranteze rotunde. Din acest motiv, muchiile și lanțurile se notează folosind paranteze pătrate, în timp ce arcele și drumurile se notează folosind paranteze rotunde. Din acest punct de vedere, diferența dintre lanțuri și drumuri este că un lanț este același atât citit de la stânga la dreapta, cât și de la dreapta la stânga.
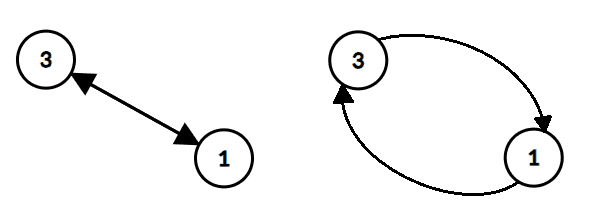
Reprezentarea grafică a unui graf este alcătuită din niște cerculețe etichetate (nodurile), unite prin segmente (muchiile/arcele). Segmentele sunt orientate dacă graful este orientat, adică pe ele se pune o săgeată care indică sensul arcului. Dacă între două noduri există ambele arce, se desenează două linii curbate cu săgeată, sau un singur segment, cu săgeată la ambele capete.
Prin subgraf cu proprietatea $P$ maximal înțelegem că dacă am mai adăuga la el un nod, împreună cu muchiile incidente la acesta, proprietatea $P$ nu ar mai fi respectată.
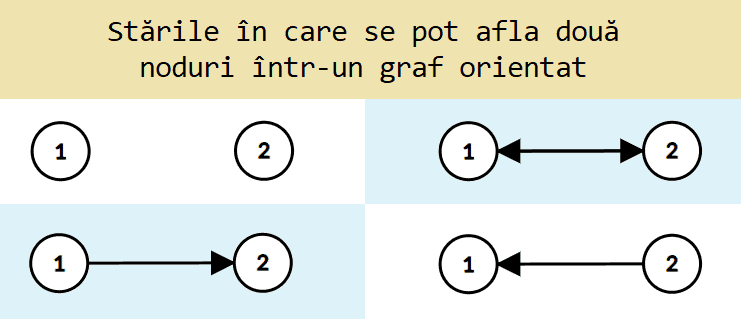
Pentru demonstrația celor mai multe formule am folosit tehnica următoare: Asociez bijectiv grafului o funcție $f : A \to B$ unde $A$ este mulțimea tuturor perechilor neordonate de noduri din $V$ iar $B$ mulțimea tuturor stărilor în care se poate afla o astfel de pereche. Numărul de grafuri va fi egal cu numărul de funcții $f$ care este dat de formula $|B|^{|A|}$

Acestea sunt noțiunile elementare din teoria grafurilor. Puteți citi în continuare despre reprezentarea grafurilor în C++. Dacă aveți vreo întrebare despre grafuri, o puteți adresa printr-un comentariu mai jos :smile: