Matrice în C++ – Tablouri bidimensionale

În C++, matricele reprezintă o structură de date standard, folosită pentru a stoca o colecție de date de același tip, organizate pe linii și coloane. Practic, o matrice este extinderea la două dimensiuni a unui vector, de unde și numele alternativ de tablou bidimensional. De asemenea, matricele pot fi privite drept vectori cu elemente de tip vector. (Cu condiția ca vectorii din urmă să nu conțină și ei la rândul lor elemente de tip vector, căci în acest caz am vorbi despre tablouri cu mai mult de două dimensiuni).

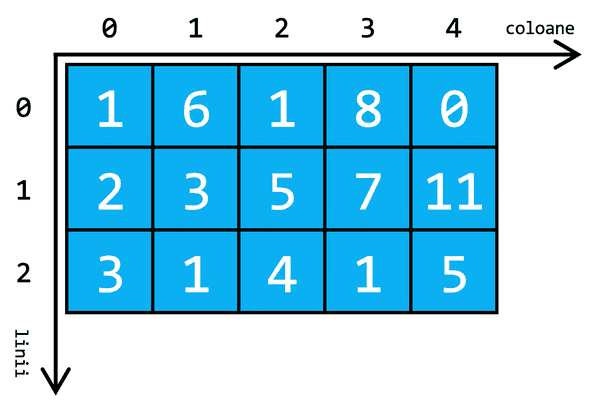
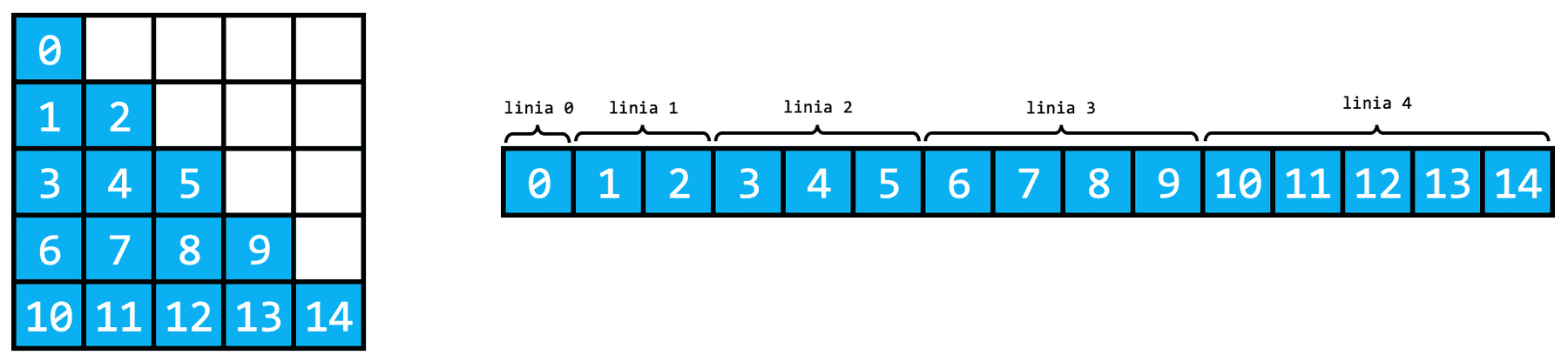
Iată mai sus reprezentarea grafică a unei matrice cu $3$ linii și $5$ coloane. Liniile sunt dispuse de sus în jos, iar coloanele de la stânga la dreapta. Atât liniile, cât și coloanele, sunt indexate de la $0$ Fiecare element (celulă) al matricei este identificat prin linia și coloana la intersecția cărora este situat. De exemplu, elementul aflat la coordonatele $(1, 3)$ are valoarea $7$

Declararea matricelor în C++

Declararea unei matrice este similară cu cea a unui vector. Diferența este că la matrice trebuie să specificăm ambele dimensiuni (maxime):

tip nume[MMAX][NMAX];

MMAX este numărul maxim de linii, iar NMAX este numărul maxim de coloane. În urma acestei instrucțiuni, calculatorul va aloca o secvență liniară de memorie, formată din MMAX * NMAX elemente de tipul tip. Da, chiar dacă noi percepem matricea drept un obiect bidimensional, calculatorul o vede liniar, pentru că așa funcționează memoria lui.

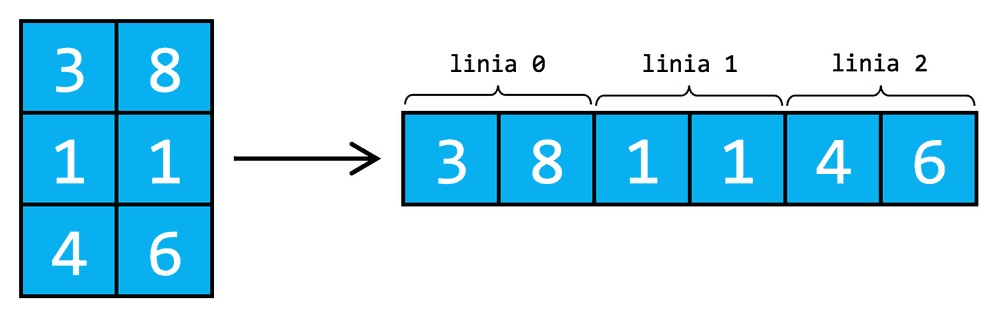
Accesarea elementelor unei matrice în C++

Pentru a accesa elementul de pe linia i și coloana j a unei matrice mat, folosim sintaxa mat[i][j]. Având în vedere că, în memoria calculatorului, matricea este stocată liniar, programul determină mai întâi, în funcție de $i$ și $j$ poziția elementului căutat în forma liniarizată a matricei, iar abia apoi accesează acel element. Formula este $i \cdot n + j$ și se poate deduce foarte ușor: Până la linia $i$ avem deja $i$ linii complete, fiecare având $n$ elemente (de aici $i \cdot n$ iar pe linia curentă avem deja $j$ elemente. Deci, elementul nostru se află la $i \cdot n + j$ elemente distanță de $(0, 0)$ Nu uitați că liniile și coloanele sunt indexate de la $0$

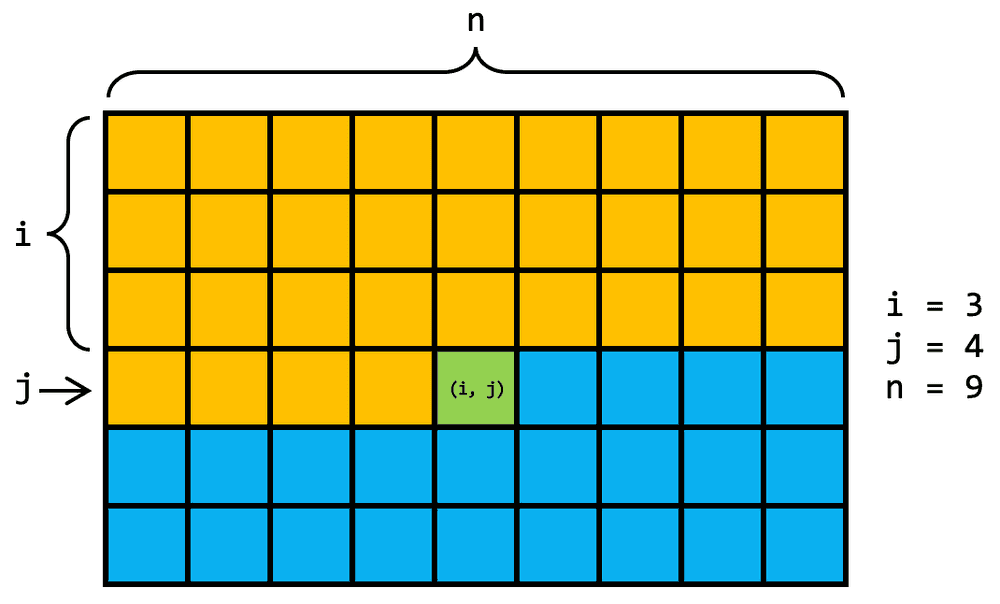
Cred că este important să înțelegem ce presupune liniarizarea unei matrice, pentru că ne ajută să percepem mai clar modul în care este structurată memoria calculatorului. În plus, odată am întâlnit o problemă în care foloseam doar jumătate din elementele unei matrice pătratice (din fiecare linie $i \ge 0$ aveam nevoie doar de primele $i + 1$ elemente), și nu aveam suficientă memorie ca să rețin toată matricea. Prin urmare, a fost nevoie să o liniarizez manual: Să o transform într-un vector și să determin o formulă particulară pentru accesarea elementelor.

Inițializarea matricelor în C++

Atunci când sunt declarate global, matricele sunt inițializate cu zero, iar atunci când sunt declarate local, cu valori aleatoare de pe stivă. Însă, dacă dorim să le inițializăm cu anumite valori, procedăm cam ca la inițializarea vectorilor. De exemplu:

int mat[5][7] = {
    {6, 1, 8},
    {1, 2, 3, 4},
    {},
    {3, 1}
};

Liniile pentru care nu am precizat niciun set de valori, precum și elementele lipsă din vectorii de lungime mai mică decât numărul de coloane ale matricei vor fi inițializate cu zero, indiferent de scopul matricei (local sau global). Deci, în urma inițializării de mai sus, matricea mat va arăta așa:

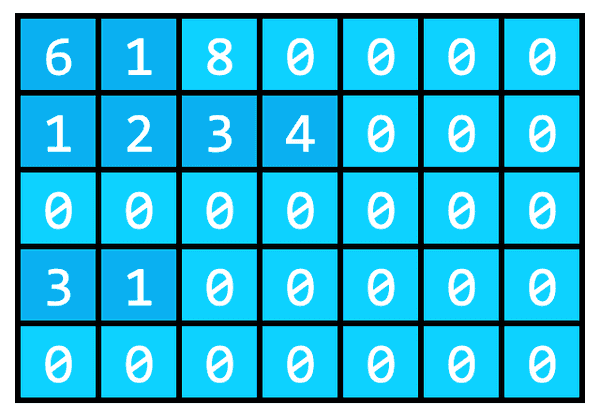
Specificarea primei dimensiuni a matricei este opțională atunci când o inițializăm. Compilatorul va considera că matricea are atâtea linii câți vectori am enumerat între acolade. A doua dimensiune însă – numărul de coloane – este obligatorie. Compilatorul are nevoie de $n$ pentru a-l putea înlocui în formula $i \cdot n + j$ folosită la accesarea de elemente ale matricei. Astfel, compilatorul poate completa matricea chiar în timp ce parsează declarația ei.

Parcurgerea unei matrice în C++

Pentru a parcurge o matrice linie cu linie și coloană cu coloană (în cadrul fiecărei linii) folosim două for-uri imbricate și doi iteratori: i pentru linie și j pentru coloană. Iată un program în C++ care citește și afișează elementele unei matrice cu m linii și n coloane:

#include <iostream>
using namespace std;

#define MMAX 314 // numărul maxim de linii
#define NMAX 618 // numărul maxim de coloane

int m, n; // numărul de linii și numărul de coloane
int mat[MMAX][NMAX]; // matricea

int main() {
    int i, j; // iteratorii pentru linie și coloană
    cin >> m >> n; // citirea dimensiunilor matricei

    // citirea elementelor matricei
    for (i = 0; i < m; i++) // linie cu linie
        for (j = 0; j < n; j++) // coloană cu coloană
            cin >> mat[i][j];

    // afișarea elementelor matricei
    for (i = 0; i < m; i++) { // linie cu linie
        for (j = 0; j < n; j++) // coloană cu coloană
            cout << mat[i][j] << ' ';
        cout << '\n';
    }
    return 0;
}

Matrice pătratice

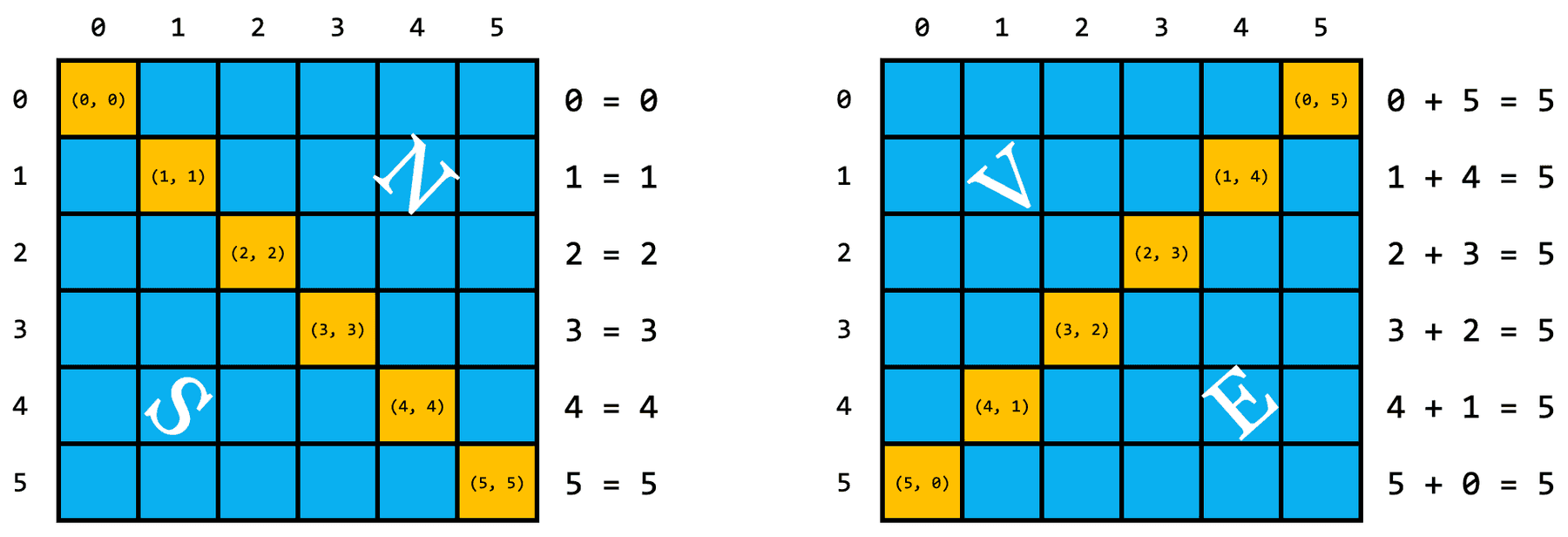
O matrice se numește pătratică dacă numărul său de linii este egal cu cel de coloane. Din pricina formei unei astfel de matrice, se pot defini două noțiuni importante: diagonala principală și diagonala secundară. Diagonala principală a unei matrice pătratice pornește din colțul stânga-sus și se termină în cel din dreapta-jos, conținând elementele de coordonate $(i, j)$ cu proprietatea $i = j$ Diagonala secundară pornește din colțul dreapta-sus și se termină în stânga-jos, conținând elementele pentru care $i + j = n - 1$ (dacă matricea e indexată de la $(0, 0)$ sau $i + j = n + 1$ (dacă matricea e indexată de la $(1, 1)$ Aceste relații între indici se numesc invarianți și se pot deduce foarte ușor; nu trebuie învățați pe de rost.

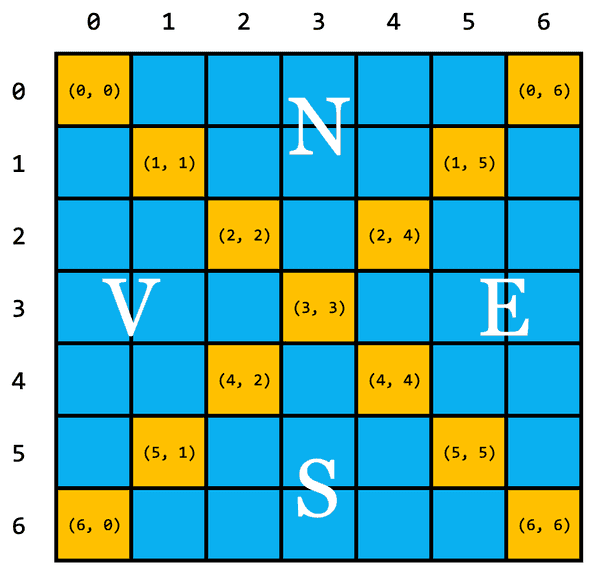
Dacă desenăm o singură diagonală, putem împărți matricea în două zone: nord și sud sau est și vest (trei dacă numărăm și diagonala). Dacă desenăm ambele diagonale, obținem patru zone: nord, est, sud și vest (cinci cu diagonala). Elementele dintr-o astfel de zonă respectă și ele diverși invarianți, permițându-ne să localizăm zona din care face parte un anumit element folosindu-ne de coordonatele sale. Despre acești invarianți voi vorbi mai mult într-un articol viitor cu probleme simple legate de matrice.

Tablouri multidimensionale în C++

Uneori avem nevoie de tablouri cu mai mult de două dimensiuni. Sintaxa lor este pur și simplu o generalizare a celei de la matrice. Atât la declarare, cât și la accesare, trebuie să menționăm toate dimensiunile tabloului, fiecare între paranteze pătrate.

Nu e greu de înțeles de ce am avea nevoie de un tablou tridimensional, deoarece ni-l putem imagina drept un paralelipiped dreptunghic format din $m \times n \times k$ cubulețe. Dar, când vine vorba de tablouri cu mai mult de trei dimensiuni, s-ar putea să ne blocăm, pentru că trăim într-un univers tridimensional (excluzând timpul), și este imposibil să ne imaginăm obiecte cu patru sau mai multe dimensiuni. Însă nici nu e nevoie!

Un exemplu ușor de înțeles este cel în care vrem să reținem un anumit lucru despre fiecare minut din cadrul unui an calendaristic. Prețul unei acțiuni la Apple de exemplu. Pentru asta, putem folosi o matrice cu patru dimensiuni. Prima ar reprezenta luna, a doua ziua, a treia ora și a patra minutul. De exemplu, aapl[6][18][3][14] reprezintă prețul unei acțiuni la data de 18 iunie, ora 03:14, și anume 351.59 USD. Declararea matricei aapl este double aapl[13][32][24][60];. Pentru simplitate, primele două dimensiuni sunt indexate de la 1, iar ultimele două de la 0.

La ce putem folosi o matrice?

Rolul general al unei matrice este cel de a reține date aferente tuturor punctelor din plan $(x, y)$ cu $0 \le x \lt m$ și $0 \le y \lt n$ Putem asocia ce semnificație vrem axelor $OX$ și $OY$ iar punctele nu trebuie să fie neapărat puncte.

Harta unei livezi

Majoritatea problemelor clasice cu matrice încep în stilul următor:

Paftenie avea o livadă cu pomi fermecați. Fiind pasionat de matematică, Paftenie a plantat în mod riguros pomii pe $m$ rânduri dispuse paralel, iar pe fiecare rând a plantat $n$ pomi echidistanți. Fiecare pom poate fi identificat prin rândul pe care se află și poziția sa în cadrul rândului respectiv. Pomii pot fi de trei feluri: meri, peri sau vișini.

Asta înseamnă:

Se dă o matrice de dimensiuni $m \times n$ cu elemente din mulțimea $\{1, 2, 3\}$

Stocarea unei imagini

Un exemplu similar este cel în care vrem să stocăm o imagine alb-negru. Pentru fiecare pixel de coordonate $(x, y)$ putem reține nuanța sa de alb, pe o scară de la $0$ la $255$ Dacă imaginea ar fi coloră, atunci ar trebui să reținem câte trei numere pentru fiecare pixel – nuanțele de roșu, verde și albastru. Din acest motiv, am putea folosi un tablou tridimensional, una dintre dimensiuni reprezentând culoarea la care facem referire. Totuși, mai elegant este să definim un struct cu trei câmpuri (r, g, b) și să declarăm o matrice cu elemente de acest tip.

Că tot am adus vorba… Când avem de a face cu un tablou în care o dimensiune este mult mai mică decât celelalte, este bine să alegem ca aceasta să fie prima. Dintr-un motiv mai greu de explicat, calculatorul va efectua mai repede accesările elementelor dacă facem optimizarea asta.

O tablă de șah

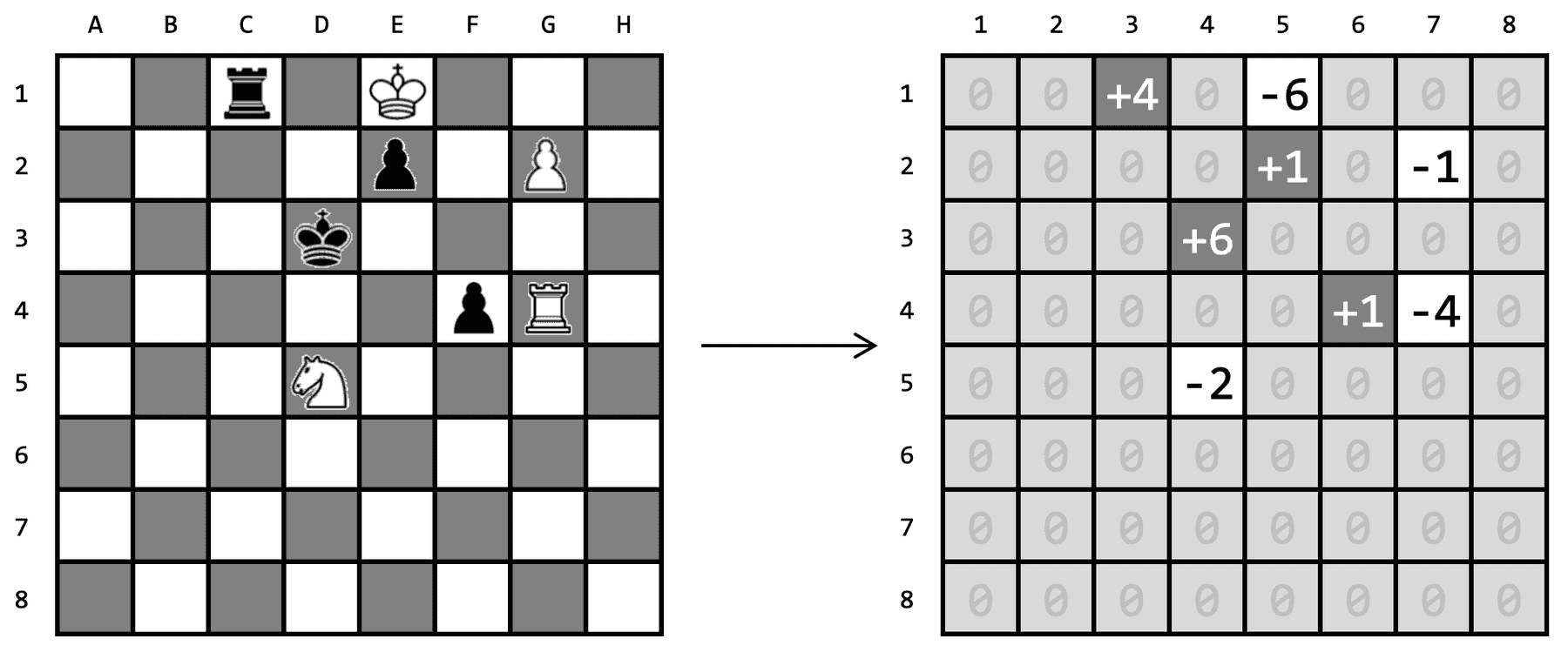
Un alt context în care matricele se dovedesc utile este simularea unui meci de șah. Putem modela tabla de joc drept o matrice pătratică cu $8$ linii și $8$ coloane. Valoarea unui element ar putea fi $0$ dacă pătrățelul respectiv este liber, sau $\pm k$ unde $k$ este un număr natural nenul ce reprezintă codul piesei respective $\htmlClass{katexified}{(} 1$ pentru pion, $2$ pentru cal etc.), iar semnul se referă la culoarea piesei (alb sau negru).

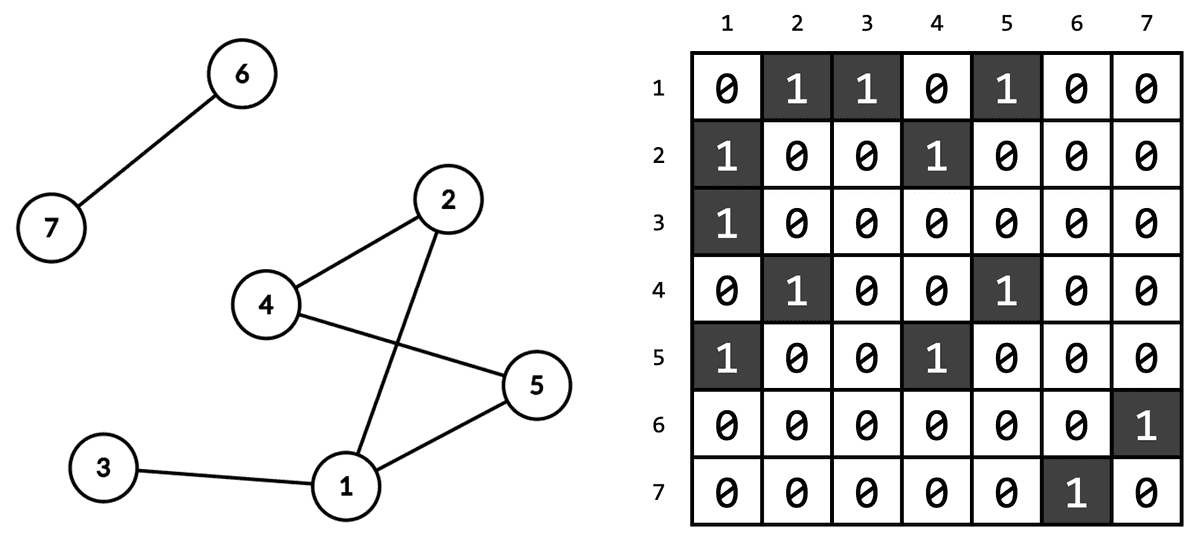
Matrice de adiacență

Matricele pătratice mai pot fi folosite pentru a modela relațiile dintre elementele unei mulțimi. Să presupunem că avem $n$ persoane și vrem să reprezentăm relațiile lor de prietenie. Putem folosi o matrice cu $n$ linii și $n$ coloane, ale cărei elemente să aparțină mulțimii $\{0, 1\}$ (matrice binară). Astfel, $\mathrm{mat}[i][j] = 1$ dacă și numai dacă $i$ și $j$ sunt prieteni. Acest tip de matrice se numește matrice de adiacență și se studiază în contextul teoriei grafurilor, unde este foarte utilă.

Matrice matematică

Nu în ultimul rând, într-un tablou bidimensional putem reține o… matrice matematică. În matematică, matricele au foarte multe aplicații, putându-ne ajuta să rezolvăm în $O(n^3)$ sisteme de ecuații liniare și să generăm în $O(\log n)$ anumiți termeni din Șirul lui Fibonacci.

Sper că v-am făcut o idee despre utilitatea matricelor în C++. Urmează în curând un articol cu probleme simple ce folosesc matrice. Dacă aveți vreo întrebare legată de matrice în C++, o puteți adresa mai jos, într-un comentariu