Problema comis-voiajorului în C++ [Backtracking]

Problema comis-voiajorului (Travelling Salesman Problem, prescurtat TSP) este o problemă clasică de backtracking elementar. Totodată, aceasta este o celebră problemă NP-completă, fiind foarte importantă în studiul informaticii teoretice. În acest articol voi prezenta abordarea problemei prin backtracking și optimizarea soluției utilizând branch and bound. Voi folosi câteva noțiuni din teoria grafurilor, dar nu este obligatoriu să le cunoașteți pentru a înțelege rezolvarea problemei.

Enunț

Se dau $n$ orașe, numerotate de la $1$ la $n$ și o listă cu $m$ străzi bidirecționale (pe care se poate circula în ambele sensuri), identificate prin cele două orașe-extremități și prin lungime. Un comis-voiajor are misiunea de a livra colete în toate aceste orașe, cu condiția să se întoarcă în orașul din care a plecat. El poate realiza asta în multe moduri, însă îl interesează un drum de lungime minimă. Așadar, se cere determinarea unui drum de lungime minimă, care să treacă prin fiecare oraș exact o singură dată, iar din ultimul oraș vizitat să revină în primul.

Exemplu

De pe prima linie a fișierului tsp.in se citesc $n$ și $m$ numărul de orașe și respectiv numărul de străzi. Pe fiecare dintre următoarele $m$ linii se găsesc câte trei numere $x$ $y$ și $z$ cu semnificația că strada dintre orașele $x$ și $y$ are lungimea $z$

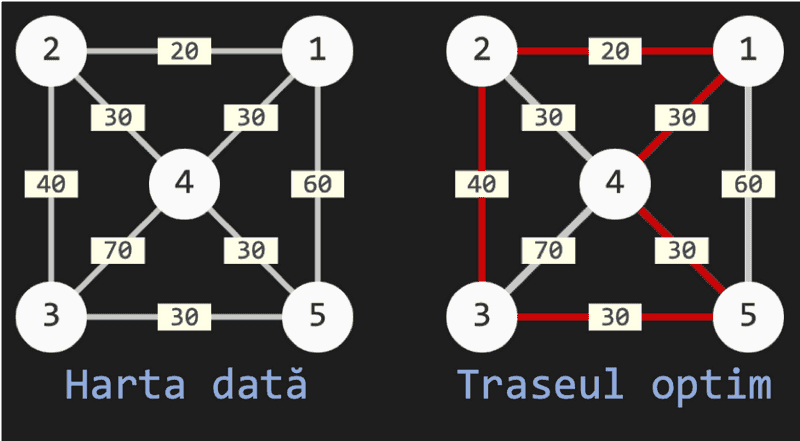
5 8
1 2 20
1 5 60
1 4 30
2 4 30
4 3 70
2 3 40
4 5 30
5 3 30

În fișierul tsp.out se va afișa pe prima linie lungimea minimă a unui traseu optim, iar pe a doua linie un astfel de traseu.

150
1 2 3 5 4

Iată cum arată harta orașului descris, precum și un drum optim pentru comisul-voiajor:

Legătura cu teoria grafurilor

Practic, ni se dă un graf neorientat cu costuri pe muchii, și trebuie să determinăm un ciclu hamiltonian (un drum care trece prin toate nodurile grafului și se întoarce în nodul inițial) de cost minim. Desigur, prin costul ciclului mă refer la suma costurilor muchiilor din care acesta este format.

Soluție prin backtracking

Folosind metoda backtracking, vom genera toate ciclurile hamiltoniene ale grafului dat, și îl vom reține pe parcurs pe cel de cost minim.

Vom reprezenta graful printr-o matrice de adiacență, adică o matrice $\mathrm{ad}$ în care pe $\mathrm{ad}[i][j]$ reținem $0$ dacă nu există stradă între orașele $i$ și $j$ sau lungimea străzii respective în caz contrar. De asemenea, în variabila $\mathrm{lg}$ vom reține lungimea traseului curent, iar în vectorul $\mathrm{tr}$ orașele din care este compus acesta. În plus, vom avea nevoie de o variabilă $\mathrm{lgMin}$ și de un vector $\mathrm{trMin}$ pentru stocarea traseului minim și a lungimii acestuia.

Acum urmează partea de backtracking. În primul rând, se observă ușor că nu contează din ce oraș pornim, pentru că oricum trebuie să ne întoarcem de unde am plecat; de exemplu, traseul $[3, 2, 5, 1]$ este tot una cu $[5, 1, 3, 2]$ Prin urmare, vom fixa pe $\mathrm{tr}[1]$ valoarea $1$ (adică vom porni mereu din orașul $1$ și vom începe generarea prin backtracking de la poziția $2$ Această idee va reduce de $n$ ori numărul de trasee generate!

Vom defini funcția de backtracking cu antetul void bkt(int pos), unde $pos$ reprezintă poziția curentă din traseul pe care îl generăm. Dacă nu am ajuns pe poziția $n + 1$ înseamnă că nu am terminat generarea. În cazul acesta, vom pune pe poziția $\mathrm{tr}[pos]$ pe rând, fiecare oraș care încă nu a fost vizitat, dar pentru care există stradă de la el la $\mathrm{tr}[pos - 1]$ Ca să ținem evidența orașelor vizitate, vom mai lua un vector caracteristic $\mathrm{vis}$ unde $\mathrm{vis}[i]$ este true dacă orașul $i$ a fost vizitat, sau false în caz contrar.

for (int i = 2; i <= n; i++)
    if (!vis[i] && ad[tr[pos - 1]][i]) {
        vis[tr[pos] = i] = true; // Adăugăm i la traseu și îl marcăm ca vizitat.
        lg += ad[tr[pos - 1]][i]; // Actualizăm lungimea traseului curent.
        bkt(pos + 1); // Continuăm generarea.
        vis[i] = false; // Restaurăm vis[i].
        lg -= ad[tr[pos - 1]][i]; // // Restaurăm lg.
    }

Dacă am ajuns în schimb la poziția $n + 1$ înseamnă că am terminat generarea unui traseu. Acum trebuie să ne întoarcem în orașul inițial. Deci, vom verifica dacă există stradă de la $1$ la $\mathrm{tr}[n]$ Dacă nu, traseul nu este valid. Dacă da, mai rămâne să adăugăm la lungime costul ultimei muchii a ciclului, adică $\mathrm{ad}[\mathrm{tr}[n]][1]$ Apoi comparăm $\mathrm{lg}$ cu $\mathrm{lgMin}$ și actualizăm soluția dacă este cazul.

if (pos == n + 1) {
    if (!ad[tr[n]][1])
        return;
    lg += ad[tr[n]][1];
    if (lg < lgMin) { // Actualizăm soluția:
        lgMin = lg;
        for (int i = 1; i <= n; i++)
            trMin[i] = tr[i];
    }
    lg -= ad[tr[n]][1];
    return;
}

Optimizare prin branch and bound

Se observă ușor că, dacă la un apel al funcției bkt lungimea curentă este mai mare sau egală cu lungimea minimă obținută până atunci, sigur acel început de traseu nu va duce la o soluție mai bună decât cea pe care o avem deja. În acest caz, putem ieși din apel printr-un simplu return.

if (lg >= lgMin)
    return;

Acest procedeu de optimizare se numește branch and bound, și se aplică adesea problemelor de backtracking în care trebuie să determinăm un cost minim. El reduce crucial timpul de execuție a programului, deoarece sare peste o grămadă de trasee nefolositoare.

Mai jos este o animație făcută de mine, care ilustrează modul în care funcționează backtracking-ul în această problemă:

Sursă C++

Iată o sursă în C++ ce rezolvă problema comis-voiajorului prin backtracking.

#include <fstream>
using namespace std;
const int DMAX = 100;

ifstream fin("tsp.in");
ofstream fout("tsp.out");

int n, m;
int ad[DMAX][DMAX];

int lgMin = 1e9;
int trMin[DMAX];

int lg;
int tr[DMAX];
bool vis[DMAX];

void bkt(int pos) {
    if (lg >= lgMin)
        return;
    if (pos == n + 1) {
        if (!ad[tr[n]][1])
            return;
        lg += ad[tr[n]][1];
        if (lg < lgMin) {
            lgMin = lg;
            for (int i = 1; i <= n; i++)
                trMin[i] = tr[i];
        }
        lg -= ad[tr[n]][1];
        return;
    }
    for (int i = 2; i <= n; i++)
        if (!vis[i] && ad[tr[pos - 1]][i]) {
            vis[tr[pos] = i] = true;
            lg += ad[tr[pos - 1]][i];
            bkt(pos + 1);
            vis[i] = false;
            lg -= ad[tr[pos - 1]][i];
        }
}

int main() {
    fin >> n >> m;
    for (int i = 0; i < m; i++) {
        int x, y, z; fin >> x >> y >> z;
        ad[x][y] = ad[y][x] = z;
    }
    vis[tr[1] = 1] = true;
    bkt(2);

    fout << lgMin << '\n';
    for (int i = 1; i <= n; i++)
        fout << trMin[i] << ' ';
    fout << '\n';
    return 0;
}

Complexitate

În cel mai nefavorabil caz, numărul total de cicluri hamiltoniene ale grafului dat este $(n - 1)! / 2$ asta se întâmplă atunci când graful este complet. Există cazuri în care, chiar și cu optimizarea făcută prin branch and bound, vom fi nevoiți să generăm toate aceste cicluri; de exemplu atunci când graful este complet și toate muchiile au același cost.

Prin urmare, complexitatea algoritmului este $O(n!)$ Teoretic, este o complexitate foarte proastă, însă în practică (pe teste obișnuite, cu $n$ până în $20$ - $30$ algoritmul se comportă destul de bine. Există și o soluție ce folosește programare dinamică, de complexitate exponențială, însă nu este foarte practică din cauza cantității mare de spațiu necesară. Voi analiza această abordare într-un articol viitor.

Problema comis-voiajorului se găsește în arhiva educațională de pe InfoArena, sub numele de Ciclu hamiltonian de cost minim. Acolo este gândită pentru grafuri orientate, indexate de la $0$ Deci, sursa de mai sus trebuie modificată un pic ca să funcționeze pe InfoArena. Oricum, va obține doar 70 de puncte; pentru restul trebuie folosită programare dinamică.

Dacă aveți vreo întrebare legată de problema comis-voiajorului, nu ezitați să o adresați într-un comentariu, mai jos