Subsecvența de sumă maximă în C++

de Iulian Oleniuc | 17/04/2020 | Algoritmică și structuri de date, Programare dinamică

Subsecvența de sumă maximă este o problemă clasică de programare dinamică, întâlnită adesea la concursurile de informatică, într-o formă sau alta. În acest articol voi prezenta o soluție în $O(n \log n)$ bazată pe divide et impera, și două soluții în $O(n)$ dintre care una folosește programare dinamică. De asemenea, voi arăta și cum putem rezolva eficient extinderea problemei la două dimensiuni.

Enunț

Se dă un vector $v$ cu $n$ elemente întregi, indexate de la $1$ Să se determine suma maximă a elementelor unei subsecvențe a vectorului dat, precum și o astfel de subsecvență. O subsecvență a vectorului $v$ reprezintă o succesiune de elemente de forma $\langle v[i], v[i+1], \ldots, v[j] \rangle$ cu $1 \le i \le j \le n$

Putem la fel de bine ca în loc de subsecvență să-i spunem doar secvență, dar având în vedere că în literatura de specialitate problema se numește Maximum Sum Subsequence, am păstrat termenul de subsecvență. Apropo, cuvântul este subsequence deoarece sequence este șirul de numere.

De exemplu, pentru $v = \langle 5, -1, 2, 4, -2, -5, 7 \rangle$ o subsecvență de sumă maximă este $\langle 5, -1, 2, 4 \rangle$ suma elementelor acesteia fiind $10$ Soluția nu este neapărat unică. Pentru acest exemplu, o altă subsecvență de sumă maximă este $\langle 5, -1, 2, 4, -2, -5, 7 \rangle$ care se întâmplă să fie întreg vectorul.

Soluții naive

O soluție imediată este să calculăm suma fiecărei subsecvențe în parte și să reținem pe parcurs suma maximă. Numărul de subsecvențe ale unui vector cu $n$ elemente este $n(n+1)/2$ Putem demonstra asta foarte ușor, observând că numărul de subsecvențe care se termină pe poziția $j$ $\htmlClass{katexified}{(} 1 \le j \le n$ este $j$ căci începutul poate lua orice valoare din mulțimea $\{1, 2, \ldots, j\}$ Având în vedere că fiecărei subsecvențe îi calculăm suma elementelor în timp liniar, complexitatea finală a algoritmului devine $O(n^3)$

int ans = -2e9;
for (int i = 1; i <= n; i++)
    for (int j = i; j <= n; j++) {
        int sum = 0;
        for (int k = i; k <= j; k++)
            sum += v[k];
        ans = max(ans, sum);
    }

Putem optimiza această soluție calculând suma elementelor unei subsecvențe cu capătul din stânga fixat în $i$ pe măsură ce ne extindem în dreapta cu capătul $j$ Astfel, obținem un algoritm în complexitate $O(n^2)$ ceea ce, în continuare, nu este mulțumitor.

int ans = -2e9;
for (int i = 1; i <= n; i++) {
    int sum = 0;
    for (int j = i; j <= n; j++) {
        sum += v[j];
        ans = max(ans, sum);
    }
}

Soluție în $O(n \log n)$ – Divide et impera

Soluția în $O(n \log n)$ folosește paradigma divide et impera, fiind un algoritm ce ilustrează foarte bine principiul acestei metode de programare. Chiar dacă soluția nu este optimă, nu înseamnă că nu e utilă. Combinată cu un arbore de intervale, această metodă poate fi folosită pentru a rezolva probleme în care trebuie să găsim eficient subsecvența de sumă maximă pe anumite intervale dintr-un vector.

Iată deci cum funcționează algoritmul:

Divide: Împărțim vectorul în două părți aproximativ egale.
Stăpânește: Calculăm recursiv subsecvența de sumă maximă din fiecare jumătate.
Combină: Subsecvența de sumă maximă din întreg vectorul se poate afla fie în prima jumătate $\htmlClass{katexified}{(} j \le [n/2]$ fie în a doua jumătate $\htmlClass{katexified}{(} i \gt [n/2]$ fie începe în prima jumătate și se termină în a doua $\htmlClass{katexified}{(} 1 \le i \le [n/2] \lt j \le n$ Valorile corespunzătoare primelor două cazuri au fost calculate deja la pasul precedent. Pentru a rezolva al treilea caz, procedăm astfel: Îl fixăm pe $i$ în $[n/2]$ și pe $j$ în $[n/2]+1$ Îl decrementăm pe $i$ până la $1$ ținând pe parcurs suma maximă a unei secvențe care începe în $i$ și se termină în $[n/2]$ Procedăm similar și cu $j$ Adunând cele două sume, obținem rezultatul pentru al treilea caz. Nu ne mai rămâne decât să calculăm maximul dintre cele trei valori.

Desigur, cazul de bază este acela când secvența curentă are un singur element. În acest caz, returnăm respectiva valoare. Iată mai jos o implementare elegantă a acestei soluții. Funcția $\mathrm{dei}$ se apelează inițial cu parametrii $1$ și $n$

int dei(int l, int r) {
    if (l == r)
        return v[l];
    int bstL = -2e9, sumL = 0;
    for (int i = (l + r) / 2; i >= l; i--)
        bstL = max(bstL, sumL += v[i]);
    int bstR = -2e9, sumR = 0;
    for (int j = (l + r) / 2 + 1; j <= r; j++)
        bstR = max(bstR, sumR += v[j]);
    return max(bstL + bstR, max(
        dei(l, (l + r) / 2),
        dei((l + r) / 2 + 1, r)
    ));
}

Complexitate

La fel ca majoritatea algoritmilor divide et impera, avem de a face cu o complexitate de ordinul $O(n \log n)$ lucru care poate fi observat ușor din arborele de execuție al funcției $\mathrm{dei}$

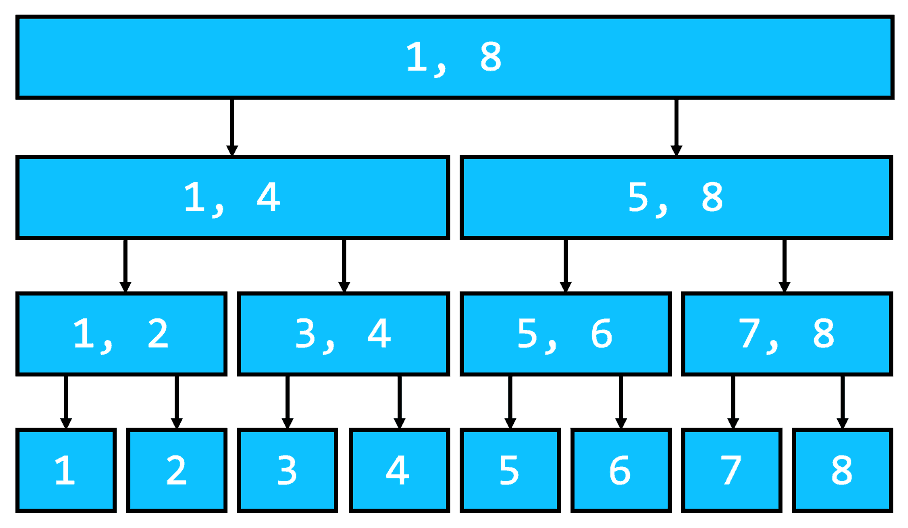
Pe fiecare nivel, suma lungimilor secvențelor corespunzătoare apelurilor este $n$ Cum pentru fiecare apel $\mathrm{dei}(l, r)$ în etapa combină efectuăm $r - l + 1$ pași, complexitatea totală pe un nivel este $O(n)$ În plus, adâncimea arborelui este aproximativ $[\log_2 n]$ iar de aici putem trage concluzia că algoritmul nostru are complexitatea $O(n \log n)$

Soluție în $O(n)$ – Sume parțiale

Soluția următoare folosește doar conceptul de sume parțiale, și dintr-un motiv sau altul este destul de nepopulară. Probabil e mai șmecher să folosești programare dinamică :tongue: Să notăm cu $s_i$ $\htmlClass{katexified}{(} 0 \le i \le n$ a $i$ a sumă parțială a lui $v$ Avem $s_i = v[1] + v[2] + \cdots + v[i]$ pentru $i \gt 0$ iar $s_0 = 0$ Astfel, putem afirma că suma subsecvenței $v[i..j]$ este egală cu $s_j - s_{i-1}$ Deci, suma maximă a unei subsecvențe ce se termină în $j$ se obține scăzând din $s_j$ cea mai mică sumă parțială $s_{i-1}$ cu $1 \le i \le j$

Așadar, ideea este să parcurgem vectorul menținând suma prefixului curent $\htmlClass{katexified}{(} ps$ cât și suma parțială minimă din acest prefix $\htmlClass{katexified}{(} mn$ La fiecare pas calculăm suma maximă a unei subsecvențe ce se termină pe poziția curentă și actualizăm maximul global dacă e cazul. Complexitatea este în mod evident $O(n)$ Iată implementarea acestei metode:

int ans = -2e9, ps = 0, mn = 0;
for (int i = 1; i <= n; i++) {
    ps += v[i];
    ans = max(ans, ps - mn);
    mn = min(mn, ps);
}

Soluție în $O(n)$ – Programare dinamică

Această soluție folosește metoda programării dinamice și se numește Algoritmul lui Kadane. Dacă nu sunteți familiarizați cu programarea dinamică, nu este o problemă, aceasta fiind poate cea mai simplă formă posibilă de dinamică. Din nou, ideea este să calculăm pentru fiecare poziție $i$ din vector suma maximă a unei subsecvențe ce se termină în $i$ Vom nota această valoare cu $\mathrm{dp}[i]$ Recurența este următoarea:

\mathrm{dp}[i] = \begin{cases} \max(\mathrm{dp}[i - 1] + v[i], v[i]) & \text{pentru } i \ge 1\\ 0 & \text{pentru } i = 0 \end{cases}

Explicația este simplă: Răspunsul pentru $i$ poate fi obținut din cel pentru $i - 1$ adăugând elementul $v[i]$ însă $\mathrm{dp}[i - 1]$ s-ar putea să fie negativ, caz în care este mai bine să considerăm doar elementul curent.

vector<int> dp(n + 1);
int ans = -2e9;
for (int i = 1; i <= n; i++) {
    dp[i] = max(dp[i - 1], 0) + v[i];
    ans = max(ans, dp[i]);
}

Putem reduce complexitatea în spațiu de la $O(n)$ la $O(1)$ renunțând la vectorul $\mathrm{dp}$ și ținând în schimb o singură variabilă $sum$ egală cu valoarea stării precedente $\htmlClass{katexified}{(} \mathrm{dp}[i - 1]$

int ans = -2e9, sum = 0;
for (int i = 1; i <= n; i++) {
    sum = max(sum, 0) + v[i];
    ans = max(ans, sum);
}

Iar dacă tot am precizat în enunț că trebuie să determinăm și o subsecvență de sumă maximă, hai s-o facem măcar de data asta! Reținem în $l$ și $r$ capetele răspunsului, iar în $i$ capătul din stânga al subsecvenței curente de sumă maximă.

int ans = -2e9, l = 0, r = 0;
int sum = 0, i = 0;
for (int j = 1; j <= n; j++) {
    if (sum > 0)
        sum += v[j];
    else {
        i = j;
        sum = v[j];
    }
    if (sum > ans) {
        ans = sum;
        l = i;
        r = j;
    }
}

Extinderea la 2D

Enunțul problemei noastre se poate extinde la două dimensiuni astfel: Dându-se o matrice $a$ cu $m$ linii și $n$ coloane, să se determine suma maximă a unei submatrice a lui $a$ De fapt chiar de aici a pornit totul: Problema inițială era cea 2D, dar pentru că nu se găseau soluții prea bune, s-a propus studiul problemei 1D pentru a înțelege mai bine mecanismul unui algoritm optim. Puteți citi aici istoricul problemei; mi se pare destul de interesant.

Soluția cea mai ineficientă are complexitatea $O(n^6)$ și presupune calcularea sumei elementelor din fiecare submatrice posibilă. O putem reduce la $O(n^4)$ precalculând sumele parțiale 2D în $O(n^2)$ Dar se poate și mai bine, generalizând una dintre soluțiile liniare pentru problema unidimensională. O voi alege pe cea cu programare dinamică.

Ideea este să ne fixăm două linii $i$ și $j$ ale matricei, și să reducem problema găsirii submatricei de sumă maximă care începe pe linia $i$ și se termină pe linia $j$ la problema găsirii subsecvenței de sumă maximă într-un vector. În acest sens, vom crea un vector $v$ de lungime $n$ cu proprietatea $v[k] = a[i][k] + a[i+1][k] + \cdots + a[j][k]$ Aplicând Algoritmul lui Kadane pentru fiecare pereche de linii $(i, j)$ cu $1 \le i \le j \le m$ și reținând maximul, am rezolvat problema în $O(n^3)$ Mă rog, dacă e să fim riguroși, este $O(m^2 n)$ Avem $O(m^2)$ de la numărul de perechi și $O(n)$ de la algoritmul liniar aplicat pentru fiecare astfel de pereche. Și de la actualizarea lui $v$ care este creat (sau inițializat cu $0$ pentru fiecare $i$

int ans = -2e9;
for (int i = 1; i <= m; i++) {
    vector<int> v(n + 1);
    for (int j = i; j <= m; j++) {
        for (int k = 1; k <= n; k++)
            v[k] += a[j][k];
        int sum = 0;
        for (int k = 1; k <= n; k++) {
            sum = max(sum, 0) + v[k];
            ans = max(ans, sum);
        }
    }
}

Iată un exemplu pentru a vizualiza mai bine algoritmul:

a = \begin{pmatrix} 1 & 2 & -1 & -4 & -20\\ -8 & \textcolor{orangered}{-3} & \textcolor{orangered}{4} & \textcolor{orangered}{2} & 1\\ 3 & \textcolor{orangered}{8} & \textcolor{orangered}{10} & \textcolor{orangered}{1} & 3\\ -4 & \textcolor{orangered}{-1} & \textcolor{orangered}{1} & \textcolor{orangered}{7} & -6 \end{pmatrix}

Submatricea de sumă maximă este cea colorată cu roșu, și are suma elementelor $29$ Vectorul $v$ asociat perechii de linii $(2, 4)$ este $\langle -9, \textcolor{orangered}{4}, \textcolor{orangered}{15}, \textcolor{orangered}{10}, -2 \rangle$ Subsecvența de sumă maximă a acestuia este $\langle 4, 15, 10 \rangle$ are suma $29$ și îi corespunde submatricei cu colțurile în $(2, 2)$ și $(4, 4)$ care este chiar răspunsul.