Admitere Informatică Iași 2015 – Subiecte și rezolvări

În acest articol voi prezenta rezolvările subiectelor date în anul 2015 la admitere la Facultatea de Informatică din Iași. Aici puteți găsi baremul. Cred că patru modele de rezolvări sunt suficiente ca să vă pregătiți pentru examenul de pe 21 iulie. Rezolvările din ultimii trei ani le găsiți la următoarele link-uri: 2018, 2017, 2016.

Subiectul I. Problema 1.

Numerele reale $x$ $y$ $z$ și $t$ satisfac inegalitățile $x \lt y$ și $z \lt t$ Precizați care dintre expresiile C++ de mai jos este echivalentă cu faptul că intervalele închise $[x, y]$ și $[z, t]$ au intersecția nevidă $\htmlClass{katexified}{(} [x, y] \cap [z, t] \neq \varnothing$

1. !((z > y) || (t < x))
2. (x <= z) || (y >= t)
3. !((x < z) && (t < y))
4. !((x > t) || (y > z))

Simplificând un pic expresiile de mai sus, folosind legile lui De Morgan (la A, B și D), obținem:

1. z <= y && t >= x
2. x <= z || y >= t
3. x >= z || t >= y
4. x <= t && y <= z

Varianta corectă este A, intersecția celor două intervale fiind $[\max(x, z), \min(y, t)]$ B este greșită pentru că returnează true când $y \lt z$ C returnează true când $x \gt t$ ceea ce iarăși nu este bine. D returnează false când $x \lt z \lt y \lt t$

Subiectul I. Problema 2.

Se consideră algoritmul de mai jos, descris în pseudocod.

citește n (număr natural)
x <- n % 10; m <- 1; s <- 1
cât timp n > 9 execută
    n <- [n / 10]; y <- n % 10
    dacă (y - x) * m < 0 atunci
        dacă m > 0 atunci
            m <- -1
        altfel
            s <- 0
    x <- y
scrie s

a) Scrieți valoarea afișată de algoritm dacă numărul $n$ citit este $213521$

Răspunsul este $0$ și iată cum se ajunge la el:

b) Care este cel mai mic număr natural format din patru cifre distincte care poate fi citit în variabila $n$ astfel încât algoritmul să afișeze valoarea $1$

Acum trebuie să înțelegem ce face de fapt algoritmul dat. Ei bine, acesta verifică dacă numărul $n$ este un munte, adică dacă cifrele sale (de la dreapta la stânga) cresc până într-un punct, iar apoi descresc. În $y$ se reține cifra curentă a lui $n$ iar în $x$ cifra precedentă. $m$ reprezintă semnul pe care trebuie să-l aibă diferența curentă dintre $y$ și $x$ Inițial aceasta trebuie să fie pozitivă, iar apoi negativă. Prin (y - x) * m < 0 se verifică dacă s-a produs o schimbare de semn a diferenței cifrelor. Dacă da, avem două cazuri: Dacă $m$ era $1$ acum trebuie să devină $-1$ însă dacă era deja $-1$ înseamnă că cifrele au reînceput să crească, încâlcând proprietatea de munte. La final, variabila $s$ ne spune dacă $n$ este munte sau nu. Deci, răspunsul la această cerință este cel mai mic număr munte format din $4$ cifre distincte, adică $1230$

c) Scrieți o secvență de instrucțiuni care să folosească doar operații de adunare și scădere și care să fie echivalentă cu instrucțiunea n <- [n / 10].

Nu este prima oară când văd o problemă dată la admitere unde trebuie folosit faptul că împărțirea este o scădere repetată. Pentru a-l împărți pe $n$ la $10$ numărăm în $cnt$ de câte ori putem scădea $10$ din el astfel încât să rămână pozitiv, iar la final, copiem valoarea din $cnt$ în $n$

cnt <- 0
cât timp n >= 10 execută
    n <- n - 10
    cnt <- cnt + 1
n <- cnt

d) Scrieți programul C++ corespunzător algoritmului dat.

Un răspuns corect este:

#include <iostream>
using namespace std;

int main() {
    int n; cin >> n;
    int x = n % 10, m = 1, s = 1;
    while (n > 9) {
        n /= 10;
        y = n % 10;
        if (m > 0)
            m = -1;
        else
            s = 0;
        x = y;
    }
    cout << s << '\n';
    return 0;
}

Subiectul II. Problema 1.

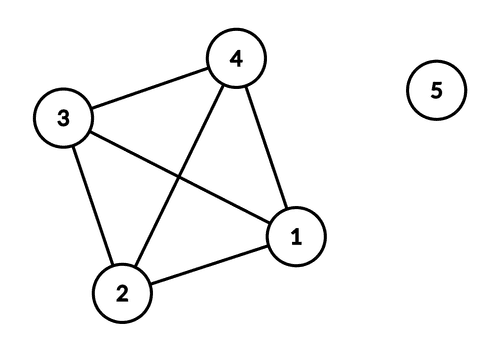
Care este numărul maxim de noduri de grad $3$ într-un graf neorientat cu $5$ noduri?

1. $2$
2. $3$
3. $4$
4. $5$

Numărul maxim de noduri de grad $3$ într-un graf neorientat cu $5$ noduri este $4$ și se atinge când $4$ dintre noduri formează un subgraf complet, iar al $5$lea nod rămâne izolat. Deci, varianta corectă este C.

Subiectul II. Problema 2.

Fie un graf neorientat cu mulțimea nodurilor $\{1, 2, \ldots, 2015\}$ Două noduri $i$ și $j$ sunt unite printr-o muchie dacă și numai dacă $\max(i, j) = 2 \min(i, j)$ sau $\max(i, j) = 2 \min(i, j) + 1$ Care este numărul de muchii ale acestui graf?

1. $2015$
2. $2016$
3. $2014$
4. $2014 \cdot 2015 \mathbin{/} 2$

Reformulând proprietatea dată, în graf există muchia $[i, j]$ cu $j \gt i$ dacă și numai dacă $[j / 2] = i$ Evident, pentru fiecare număr $j$ din mulțimea nodurilor există exact un $i$ astfel încât $[j / 2] = i$ și deci fiecărui număr îi corespunde exact o muchie. Excepție face $1$ deoarece $[1 / 2] = 0$ care nu aparține mulțimii nodurilor. Așadar, răspunsul este $2014$ varianta corectă fiind C. Se observă că graful dat este arbore, pentru că numărul muchiilor este cu $1$ mai mic decât numărul nodurilor.

Subiectul II. Problema 3.

Considerăm codificarea binară a caracterelor, în care fiecărui simbol îi revine reprezentarea pe 8 biți a codului său ASCII. De exemplu, caracterului 'A', având codul ASCII 65, îi va corespunde reprezentarea binară 01000001. Scrieți un program C++ care să conțină următoarele funcții:

1. Funcția convert_char primește ca argument un caracter și construiește un tablou cu 8 elemente 0 sau 1, reprezentând codificarea binară a caracterului primit.

2. Funcția convert_string primește ca argument un șir de caractere s și construiește o matrice cu n linii și 8 coloane (unde n este lungimea șirului s), linia i a matricei reprezentând codificarea binară a caracterului de pe poziția i din șir.

3. Funcția submatrix_size primește ca argument o matrice m formată doar din elemente 0 și 1 (precum și dimensiunile sale) și determină dimensiunea celei mai mari submatrice pătratice a lui m conținând elemente având toate aceeași valoare (fie 0, fie 1).

Observație: Funcțiile pot avea și alte argumente față de cele specificate mai sus.

Programul va citi de la tastatură un șir de caractere s și va afișa rezultatul determinat de funcția submatrix_size aplicată pe matricea construită de convert_string aplicată asupra lui s.

Exemplu: Pentru șirul de caractere s = "IDEEA", se va afișa 3, matricea corespunzătoare fiind:

$$m = \begin{pmatrix} 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1\\ 0 & 1 & \mathbf{0} & \mathbf{0} & \mathbf{0} & 1 & 0 & 0\\ 0 & 1 & \mathbf{0} & \mathbf{0} & \mathbf{0} & 1 & 0 & 1\\ 0 & 1 & \mathbf{0} & \mathbf{0} & \mathbf{0} & 1 & 0 & 1\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \end{pmatrix}$$

O problemă de implementare destul de simplă. În enunț scrie că funcțiile pot avea și alți parametri pe lângă cei dați, așa că am transmis toate tablourile ca parametri. Pentru convert_char aflu valoarea fiecărui bit al lui chr, folosind operații pe biți, și îl pun la poziția corespunzătoare în vectorul bin. În funcția convert_string nu fac decât să apelez convert_char pentru fiecare linie a matricei.

În funcția submatrix_size parcurg matricea, iar pentru fiecare poziție $(i, j)$ aflu lungimea maximă a unei submatrice pătratice cu colțul stânga-sus în $(i, j)$ Pentru asta am apelat o funcție auxiliară, ij_length. În această funcție încerc să măresc cât mai mult lungimea submatricei curente, având grijă să nu ies din matricea mare. La fiecare pas verific dacă vreun element proaspăt adăugat la submatrice este diferit de $m[i][j]$ Dacă da, lungimea actuală nu este validă, răspunsul fiind $len - 1$ La finalul funcției, trebuie de asemenea returnat $len - 1$ căci poate n-am întâmpinat niciun element diferit de $m[i][j]$ pentru nicio valoare posibilă a lui $len$

#include <cstring>
#include <iostream>

using namespace std;

const int SMAX = 100;
// (SMAX - 1) = lungimea maximă a șirului de caractere

void convert_char(char chr, bool bin[8]) {
    for (int i = 0; i < 8; i++)
        bin[7 - i] = chr & (1 << i);
}

void convert_string(char* s, bool bin[SMAX][8]) {
    for (int i = 0; s[i]; i++)
        convert_char(s[i], bin[i]);
}

int ij_length(int x, int y, bool m[SMAX][8], int i, int j) {
    for (int len = 2; i + len <= x && j + len <= y; len++)
        for (int k = 0; k < len; k++) {
            if (m[i + k][j + len - 1] != m[i][j]) return len - 1;
            if (m[i + len - 1][j + k] != m[i][j]) return len - 1;
        }
    return len - 1;
}

int submatrix_size(int x, int y, bool m[SMAX][8]) {
    int sol = 0;
    for (int i = 0; i < x; i++)
        for (int j = 0; j < y; j++) {
            int len = ij_length(x, y, m, i, j);
            if (len > sol)
                sol = len;
        }
    return sol;
}

char str[SMAX];
bool mat[SMAX][8];

int main() {
    cin >> str;
    convert_string(str, mat);
    cout << submatrix_size(strlen(str), 8, mat) << '\n';
    return 0;
}

Complexitatea funcției submatrix_size este $O(n^4)$ dar cum numărul de coloane ale matricei este limitat la $8$ o putem considera $O(n^2)$ cu o constantă foarte mare $\htmlClass{katexified}{(} 576 = 8 \cdot 36 \cdot 2$ $8$ de la $len$ul maxim, $36 \cdot 2 = (8 \cdot 9 / 2) \cdot 2$ de la verificările corespunzătoare fiecărui $len$ de la $1$ la $8$ Cred că această soluție ar fi obținut punctaj maxim, dar eu unul aș fi aplicat un algoritm mult mai bun, ce folosește programare dinamică, cu constanta $2$

Fie următoarea dinamică: $\mathrm{dp}[i][j] =$ dimensiunea maximă a unei submatrice pătratice care conține numai elemente cu valoarea $x$ și care are colțul din dreapta-jos în $(i, j)$ Recurența este destul de cunoscută:

Explicația este că $\mathrm{dp}[i - 1][j] + 1$ ne spune care e lungimea maximă pe verticală, $\mathrm{dp}[i][j - 1] + 1$ pe orizontală, iar $\mathrm{dp}[i - 1][j - 1] + 1$ pe diagonală. Dintre cele trei valori trebuie să alegem minimul, ca să fim siguri că submatricea nu conține niciun element diferit de $x$ Vom construi așadar două dinamici: una pentru $0$ și una pentru $1$ De aici vine constanta $2$ din spatele complexității de $O(n^2)$ Iată implementarea acestei idei:

int min(int x, int y, int z) {
    int mn = x < y ? x : y;
    return mn < z ? mn : z;
}

int max(int x, int y, int z) {
    int mx = x > y ? x : y;
    return mx > z ? mx : z;
}

int submatrix_size(int x, int y, bool m[SMAX][8]) {
    int sol = 1;
    int dp0[SMAX][8], dp1[SMAX][8];

    for (int j = 0; j < y; j++) { dp0[0][j] = !m[0][j]; dp1[0][j] = m[0][j]; }
    for (int i = 1; i < x; i++) { dp0[i][0] = !m[i][0]; dp1[i][0] = m[i][0]; }

    for (int i = 1; i < x; i++)
        for (int j = 1; j < y; j++) {
            dp0[i][j] = (m[i][j] ? 0 : min(dp0[i - 1][j], dp0[i][j - 1], dp0[i - 1][j - 1]) + 1);
            dp1[i][j] = (m[i][j] ? min(dp1[i - 1][j], dp1[i][j - 1], dp1[i - 1][j - 1]) + 1 : 0);
            sol = max(sol, dp0[i][j], dp1[i][j]);
        }
    return sol;
}

Subiectul II. Problema 4.

Fie mulțimea $S = \{1, 2, \ldots, n\}$ unde $n \ge 4$ este un număr natural multiplu de $4$ Scrieți un program C++ care:

1. Citește de la tastatură numărul $n \ge 4$ precum și un număr natural $p$ $\htmlClass{katexified}{(} 1 \le p \le n / 2$ În cazul în care condițiile impuse nu sunt îndeplinite, va fi afișat mesajul "date invalide".

2. Partiționează mulțimea dată $S$ în două submulțimi disjuncte $A$ și $B$ $\htmlClass{katexified}{(} S = A \cup B$ $A \cap B = \varnothing$ astfel încât suma elementelor din $A$ să fie egală cu suma elementelor din $B$

3. Elimină elementul $p$ din mulțimea $S$ și creează o nouă partiție $A', B'$ (eventual, modificând partiția creată la punctul b) astfel încât $S \setminus \{p\} = A' \cup B'$ $A' \cap B' = \varnothing$ și suma elementelor din $A'$ este egală cu suma elementelor din $B'$ În cazul în care acest lucru nu este posibil, va fi afișat mesajul "partitie inexistenta".

Exemplu: Pentru $n = 8$ $S = \{1, 2, 3, 4, 5, 6, 7, 8\}$ partiția inițială este $A = \{1, 3, 6, 8\}$ $B = \{2, 4, 5, 7\}$ Dacă $p = 1$ sau $p = 3$ va afișa "partitie inexistenta". Dacă $p = 2$ partiția modificată este $A' = \{3, 6, 8\}$ $B' = \{1, 4, 5, 7\}$ Dacă $p = 4$ partiția modificată este $A' = \{2, 6, 8\}$ $B' = \{1, 3, 5, 7\}$

Prima cerință este trivială, așa că trecem la b: Observăm că dacă cuplăm $1$ cu $n$ $2$ cu $n - 1$ $3$ cu $n - 2$ etc., obținem $n / 2$ perechi de sume egale. Cum $n$ este multiplu de $4$ $n / 2$ va fi număr par, așa că putem pune o jumătate dintre perechi în mulțimea $A$ și cealaltă jumătate în mulțimea $B$ Structura mulțimilor va fi:

Să notăm cu $sum(X)$ suma elementelor din mulțimea $X$ Prima observație cu privire la cerința c este că dacă $p$ este impar, nu există soluție. Motivul este că suma numerelor de la $1$ la $n$ (să o notăm cu $2 \cdot S$ este pară, din moment ce $n$ este multiplu de $4$ Dacă din $S$ îl scădem pe $p$ care este impar, vom obține un număr impar, deci $sum(A)$ și $sum(B)$ nu vor putea fi egale. Dacă în schimb $p$ este par, trebuie să echilibrăm cele două mulțimi astfel încât $sum(A') = sum(B') = S - p / 2$ (Din mulțimea $A$ o vom forma pe $A'$ iar din $B$ pe $B'$ Avem de analizat următoarele două cazuri:

• $p \in B$ $p \mathbin{/} 2$ impar. Avem $p \mathbin{/} 2 \in A$ așa că putem să-l mutăm pe $p \mathbin{/} 2$ din $A$ în $B$ Obținem $sum(A') = sum(A) - p \mathbin{/} 2 = S - p \mathbin{/} 2$ și $sum(B') = sum(B) - p + p \mathbin{/} 2 = S - p \mathbin{/} 2$

• $p \in B$ $p \mathbin{/} 2$ par. Avem $p \mathbin{/} 2 + 1 \in A$ Putem să-i ducem pe $p \mathbin{/} 2 + 1$ și pe $1$ din $A$ în $B$ iar pe $2$ din $B$ în $A$ Obținem astfel $sum(A') = sum(A) - p \mathbin{/} 2 - 1 - 1 + 2 = S - p \mathbin{/} 2$ și $sum(B') = sum(B) - p + p \mathbin{/} 2 + 1 + 1 - 2 = S - p \mathbin{/} 2$

Atenție la restricția $p \le n / 2$ Eu inițial n-am băgat-o în seamă, așa că am luat patru cazuri în loc de două. Pentru a înțelege pe deplin ce am făcut mai sus, trebuie să vă luați un exemplu precum $n = 16$ și să analizați pe hârtie fiecare dintre cele două cazuri. Iată cum arată implementarea în C++ a acestor idei:

#include <iostream>
using namespace std;

const int NMAX = 101;
// 2 * (NMAX - 1) = valoarea maximă a lui n

int n, p;
int lgA1, A1[NMAX], lgB1, B1[NMAX]; // A, B
int lgA2, A2[NMAX], lgB2, B2[NMAX]; // A', B'

int main() {
    cin >> n >> p;
    if (!(n >= 4 && n % 4 == 0 && 1 <= p && p <= n / 2)) {
        cout << "date invalide\n";
        return 0;
    }

    lgA1 = lgB1 = n / 2;
    for (int i = 1, j = 1; i <= n / 4; i++, j += 2) {
        A1[i] = j;
        B1[i] = j + 1;
    }
    for (int i = n / 4 + 1, j = n / 2 + 2; i <= n / 2; i++, j += 2) {
        A1[i] = j;
        B1[i] = j - 1;
    }
    cout << "A: "; for (int i = 1; i <= lgA1; i++) cout << A1[i] << ' '; cout << '\n';
    cout << "B: "; for (int i = 1; i <= lgB1; i++) cout << B1[i] << ' '; cout << '\n';

    if (p % 2) {
        cout << "partitie inexistenta\n";
        return 0;
    }
    if (p / 2 % 2) {
        for (int i = 1; i <= lgA1; i++)
            if (A1[i] != p / 2)
                A2[++lgA2] = A1[i];
        for (int i = 1; i <= lgB1; i++)
            if (B1[i] == p)
                B2[++lgB2] = p / 2;
            else
                B2[++lgB2] = B1[i];
    }
    else {
        A2[++lgA2] = 2;
        for (int i = 2; i <= lgA1; i++)
            if (A1[i] != p / 2 + 1)
                A2[++lgA2] = A1[i];
        B2[++lgB2] = 1;
        for (int i = 2; i <= lgB1; i++)
            if (B1[i] == p)
                B2[++lgB2] = p / 2 + 1;
            else
                B2[++lgB2] = B1[i];
    }
    cout << "A': "; for (int i = 1; i <= lgA2; i++) cout << A2[i] << ' '; cout << '\n';
    cout << "B': "; for (int i = 1; i <= lgB2; i++) cout << B2[i] << ' '; cout << '\n';
    return 0;
}

Subiectul III. Problema 1.

Într-o urnă se află $4$ bile de culoare albă și $3$ bile de culoare neagră. Se extrag bilele pe rând și se reține secvența de $7$ culori obținută. Câte astfel de secvențe distincte sunt?

1. $210$
2. $35$
3. $70$
4. $840$

Cum bilele sunt de doar două culori, putem spune că două secvențe de bile diferă dacă șirurile formate din pozițiile ce conțin bile albe diferă. Numărul secvențelor din urmă este $C_{4 + 3}^4 = 35$ Varianta corectă este B.

Subiectul III. Problema 2.

Pentru funcțiile F1 și F2 definite mai jos, ce valoare va returna apelul F1(34)?

int F2(int x);

int F1(int x) {
    if (x < 7)
        return 3 + x;
    else
        return 2 + F2(x - 2);
}

int F2(int x) {
    if (x < 10)
        return 3 * x;
    else
        return 2 * F1(x / 2);
}

Ca de obicei, la acest tip de exercițiu trebuie să urmărim lanțul de apeluri recursive. De data asta avem parte de o situație un pic mai specială, pentru că ni se dau două funcții indirect recursive: F1 apelează pe F2, iar F2 pe F1. Apropo, funcția F2 a trebuit declarată înainte de a defini funcția F1, pentru că în definiția ei, F1 se folosește de F2.

F1(34)
= 2 + F2(32)
= 2 + 2 * F1(16)
= 2 + 2 * (2 + F2(14))
= 2 + 2 * (2 + 2 * F1(7))
= 2 + 2 * (2 + 2 * (2 + F2(5)))
= 2 + 2 * (2 + 2 * (2 + 3 * 5))
= 74

Subiectul III. Problema 3.

Un puzzle Minesweeper este o matrice de $n$ linii și $m$ coloane care conține la fiecare poziție numărul $0$ (reprezentând un loc liber) sau $-1$ (reprezentând o mină). Pozițiile adiacente poziției $(i, j)$ sunt:

$$\small \{(i - 1, j - 1), (i - 1, j), (i - 1, j + 1), (i, j - 1), (i, j + 1), (i + 1, j - 1), (i + 1, j), (i + 1, j + 1)\}\\ \small \cap \, \{0, \ldots, n - 1\} \times \{0, \ldots, m - 1\}$$

O poziție $(i, j)$ din matrice este periculoasă dacă cel puțin o poziție din cele maxim $8$ poziții adiacente conține o mină. Fie $(l, c)$ o poziție în matrice. Zona sigură este compusă din toate pozițiile accesibile din $(l, c)$ urmând un drum format din poziții nepericuloase adiacente.

Zona activă conține toate pozițiile zonei sigure și pozițiile adiacente zonei sigure. Matricea rezultat are aceleași dimensiuni cu puzzle-ul și este definită astfel:

• Dacă $(l, c)$ conține o mină, matricea rezultat va fi chiar puzzle-ul inițial.
• Dacă $(l, c)$ nu conține o mină dar este periculoasă, matricea rezultat conține $-2$ peste tot cu excepția poziției $(l, c)$ care conține numărul de mine vecine.
• Altfel, matricea rezultat conține pe fiecare poziție $(i, j)$ din zona activă numărul de mine adiacente poziției $(i, j)$ și $-2$ în celelalte poziții.

Exemplu	(I)	(II)	(III)	(IV)
Puzzle	$\begin{pmatrix} -1 & 0 & 0 & -1\\ 0 & 0 & \mathbf{-1} & 0\\ 0 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \end{pmatrix}$	$\begin{pmatrix} 0 & 0 & 0 & 0\\ 0 & -1 & -1 & 0\\ 0 & \mathbf{0} & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix}$	$\begin{pmatrix} -1 & 0 & \mathbf{0} & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & -1 & -1\\ 0 & -1 & 0 & -1 \end{pmatrix}$	$\begin{pmatrix} -1 & 0 & 0 & 0\\ 0 & 0 & 0 & \mathbf{0}\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & -1 \end{pmatrix}$
Poziția $(l, c)$	$(1, 2)$	$(2, 1)$	$(0, 2)$	$(1, 3)$
Rezultat	$\begin{pmatrix} -1 & 0 & 0 & -1\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \end{pmatrix}$	$\begin{pmatrix} -2 & -2 & -2 & -2\\ -2 & -2 & -2 & -2\\ -2 & 2 & -2 & -2\\ -2 & -2 & -2 & -2 \end{pmatrix}$	$\begin{pmatrix} -2 & 1 & 0 & 0\\ -2 & 2 & 2 & 2\\ -2 & -2 & -2 & -2\\ -2 & -2 & -2 & -2 \end{pmatrix}$

a) Scrieți matricea rezultat pentru exemplul (IV).

Ne aflăm în cazul al treilea, pentru că poziția dată nu conține mină, și nu este nici periculoasă. Zona activă este reprezentată de toate celulele matricei, cu excepția celor cu valoarea $-1$ Pe pozițiile periculoase punem $1$ pentru că sunt adiacente cu o singură mină, în locul celor cu mină punem $-2$ iar pe celelalte le lăsăm $0$

b) Scrieți în limbajul C++ o funcție care, primind la intrare un puzzle, calculează o matrice (de aceleași dimensiuni cu puzzle-ul) care conține $0$ pe pozițiile nepericuloase și $1$ pe pozițiile periculoase.

Funcția va primi ca parametri dimensiunile n și m, și două matrice: puzzle (cea inițială), și danger (cea pe care trebuie să o construim). Pur și simplu parcurgem vecinii fiecărei celule din puzzle și verificăm dacă aceasta este vecină cu măcar o mină.

// NMAX = valoarea maximă a lui n
// MMAX = valoarea maximă a lui m

void buildDanger(int n, int m, int puzzle[NMAX][MMAX], int danger[NMAX][MMAX]) {
    // Vectorii de deplasare:
    int addLin[] = {-1, -1, 0, 1, 1, 1, 0, -1};
    int addCol[] = {0, 1, 1, 1, 0, -1, -1, -1};

    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++) {
            danger[i][j] = 0;
            for (int k = 0; k < 8; k++) {
                int x = i + addLin[k], y = j + addCol[k]; // vecinul curent
                if (!(0 <= x && x < n && 0 <= y && y < m)) // Am ieșit din matrice.
                    continue;
                if (puzzle[x][y] == -1) {
                    danger[i][j] = 1;
                    break;
                }
            }
        }
}

c) Scrieți în limbajul C++ o funcție care:

• Primește ca argument o matrice reprezentând puzzle-ul Minesweeper și poziția $(l, c)$
• Construiește matricea rezultat după cum este descris mai sus.

Verificăm mai întâi în ce situație ne aflăm. Primul caz este banal, pur și simplu copiem matricea. În al doilea caz, numărăm vecinii lui $(l, c)$ ca la punctul precedent, iar în rest punem $-2$ Cazul al treilea este mai special, pentru că trebuie să determinăm zona activă. Putem face asta printr-o parcurgere BFS pe matrice (Algoritmul lui Lee), sau printr-un DFS pe matrice (flood fill). Eu am ales să fac fill, pentru că este mai ușor de implementat, fiind o funcție recursivă.

// NMAX = valoarea maximă a lui n
// MMAX = valoarea maximă a lui m

void fill(int i, int j, int n, int m, int puzzle[NMAX][MMAX], int answer[NMAX][MMAX]) {
    int addLin[] = {-1, -1, 0, 1, 1, 1, 0, -1};
    int addCol[] = {0, 1, 1, 1, 0, -1, -1, -1};

    // Numărăm vecinii cu mină:
    answer[i][j] = 0;
    for (int k = 0; k < 8; k++) {
        int x = i + addLin[k], y = j + addCol[k];
        if (!(0 <= x && x < n && 0 <= y && y < m))
            continue;
        if (puzzle[x][y] == -1)
            answer[i][j]++;
    }

    if (answer[i][j] > 0) // Suntem pe marginea zonei active.
        return; // Vizităm pozițiile periculoase, dar nu ne expandăm din ele.

    for (int k = 0; k < 8; k++) {
        int x = i + addLin[k], y = j + addCol[k];
        if (!(0 <= x && x < n && 0 <= y && y < m))
            continue;
        if (answer[x][y] == -2) // Dacă n-am vizitat celula:
            fill(x, y, n, m, puzzle, answer);
    }
}

void buildAnswer(int n, int m, int puzzle[NMAX][MMAX], int l, int c, int answer[NMAX][MMAX]) {
    int addLin[] = {-1, -1, 0, 1, 1, 1, 0, -1};
    int addCol[] = {0, 1, 1, 1, 0, -1, -1, -1};

    if (puzzle[l][c] == -1)
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                answer[i][j] = puzzle[i][j];
    else {
        // Numărăm vecinii cu mină:
        int cnt = 0;
        for (int k = 0; k < 8; k++) {
            int x = l + addLin[k], y = c + addCol[k];
            if (!(0 <= x && x < n && 0 <= y && y < m))
                continue;
            if (puzzle[x][y] == -1)
                cnt++;
        }

        if (cnt) { // Dacă zona este periculoasă:
            for (int i = 0; i < n; i++)
                for (int j = 0; j < m; j++)
                    answer[i][j] = -2;
            answer[l][c] = cnt;
        }
        else {
            for (int i = 0; i < n; i++)
                for (int j = 0; j < m; j++)
                    answer[i][j] = -2;
            fill(l, c, n, m, puzzle, answer);
        }
    }
}

Gata și cu subiectele date la admitere în 2015. Dacă aveți vreo întrebare legată de problemele din acest articol, nu ezitați să o lăsați într-un comentariu mai jos