Best of FIICode 2021

Principalul proiect în care m-am implicat în primul an de facultate (2020-2021) a fost FIICode – un concurs de algoritmică, în stil ICPC, format din patru runde, organizat de studenții Facultății de Informatică din Iași. Prin studenții mă refer la vreo zece persoane pasionate de programare competitivă, care până la urmă au rămas în jur de patru, dintre care a patra varia de la meeting la meeting. Noroc că în ultimii doi ani ni s-a alăturat și Bicsi, care a mai venit cu niște idei de probleme mișto.

Până la urmă a fost o experiență interesantă, cu nopți dormite o oră și jumătate, enunțuri scrise în timpul rundei, teste generate la zece minute după începerea rundei… Cu cinci minute înainte de runda a treia, noi abia terminasem cu trei probleme din cinci. La una dintre cele lipsă, comisia avea trei surse. Fiecare dădea diferit – nici nu știam pe care să o folosim pentru a genera testele oficiale. O altă chestie mișto este că prin sursele concurenților am găsit comentarii de genul:

În finală chiar am scris un enunț despre Baltagul, special pentru autorul comentariului. Din păcate, nu cred că a avut ocazia să-l citească. Lăsând gluma la o parte, probabil că așa aș fi reacționat și eu dacă eram concurent. Tocmai din acest motiv, următoarea ediție FIICode va avea doar două runde. Cum zicea și proful meu de mate din liceu,

decât mult și prost, mai bine puțin și prost.

Cum am ales numele problemelor?

Știm cu toții că a stabili numele problemelor este cea mai dificilă parte din organizarea unui concurs de informatică. Asta pentru că trebuie, pe cât posibil, să potrivești numele problemei cu indexul ei în listă. Adică, numele problemei A trebuie să înceapă cu litera A, numele problemei B cu B și așa mai departe.

În prima rundă am vrut să mascăm în numele problemelor autorii lor:

1. Aisimok: Komisia scris invers. Nu întâmplător asta e prima problemă, deoarece în continuare urmează să prezentăm membrii comisiei.
2. B9i: Dacă se află pe aici vreun concurent din ediția trecută, probabil că numele ăsta e cel mai mare mister pe care vrea să-l deslușească. Ei bine, 9 scris cu cifre romane este IX. Așadar, B9i vine de la BIXi, care vine de la… Bicsi!
3. Cuinelo: Oleniuc scris invers.
4. Dr. Anei: Dacă inserăm Dr. între An și ei, obținem Andrei. Numele era cât pe ce să rămână Dr. Ian. Noroc de mine că urăsc trapperii și l-am schimbat la timp. Însă acum că mă gândesc mai bine… Dre din Dr. Dre oricum vine de la André, deci mai bine îl puneam direct pe ăsta.
5. Etianap: Panaite scris invers. A nu se confunda cu Panaete!

Pentru runda a doua am folosit niște nume legendare de echipe ICPC, primele patru fiind din FII:

1. Infinity War: Bine, nu-i o echipă tocmai legendară.
2. Lynx: Asta e echipa mea. N-avem cine știe ce rezultate împreună, dar mai vorbim după SEERC-ul următor.
3. Clown Fiesta: Prima și deocamdată ultima echipă românească din afara Bucureștiului care s-a calificat vreodată la World Finals!
4. Endgame: Posibil calificați la World Finals 2022.
5. Scrambled Eggs: Echipa lui Bicsi.

La runda a treia se vede că n-am avut prea mult timp pentru nume:

1. Alex Chills
2. Alex Counts
3. Alex Climbs
4. Alex Combines
5. Alex Concatenates

De runda finală nu mai zic:

1. Final A
2. Final B
3. Final C
4. Final D
5. Final E

Acum că mi-am epuizat toate ideile de creative writing, cred că a venit momentul să fac ceva mai tehnic, adică să rezolv(ăm) niște probleme. Deci, pentru restul articolului voi prezenta șase probleme care mi-au plăcut mie în mod deosebit. Soluțiile lor folosesc niște idei care merită reținute, și cred că reprezintă în general un antrenament bun pentru concursuri. Pentru a citi soluțiile, trebuie să completați mai întâi captcha-ul de mai jos

Infinity War

• Autor: Iulian Oleniuc
• Dificultate:
• Enunț: CSAcademy

Această problemă este un joc pe care l-am descoperit schimbând posturile de la TV șirurile random de pe OEIS. Deci ideea nu e originală, dar măcar demonstrația e făcută de mine.

Avem un joc cu două grămezi de pietre, de dimensiuni $a$ și $b$ și doi jucători, Alex și Paul, care „mută” alternativ. La fiecare pas, dacă este posibil, jucătorul curent alege o grămadă pe care o elimină, iar pe cealaltă o împarte în două grămezi mai mici, dar nevide. Jucătorul care nu mai poate muta pierde. Știind că ambele personaje joacă optim, să se determine cine câștigă jocul.

Ăsta e genul de problemă unde știi că toată soluția constă într-un if și o formulă simplă. De aceea s-au luat o grămadă de minusuri în primele minute ale rundei, lumea trimițând surse ca cea de mai jos, fără să gândească mai mult de două secunde

cout << (a % 2 ? 'P' : 'A') << '\n';

Ce-i drept, nu erau departe de formula corectă:

cout << (a % 2 && b % 2 ? 'P' : 'A') << '\n';

Demonstrație

Să vedem totuși de ce if-ul ăsta funcționează. Vom demonstra deci că Alex (primul jucător) câștigă dacă și numai dacă cel puțin una dintre grămezile inițiale conține un număr par de pietre. Să presupunem că $a$ este grămada respectivă. Ei bine, Alex poate alege să renunțe la $b$ și să-l împartă pe $a$ în $1$ și $a - 1$

Acum avem două cazuri. Dacă $a - 1 = 1$ atunci niciuna dintre cele două grămezi nu mai poate fi divizată, așa că jocul se termină și Alex câștigă. Altfel, la pasul următor, Paul va fi obligat să împartă grămada $a - 1$ în două. Însă noi știm că $a - 1$ este un număr impar! Așadar, cele două grămezi care vor rezulta din această operație vor fi cu siguranță una pară și una impară. Iar de aici, Alex poate repeta această strategie până va ajunge la configurația $(1, 1)$

Deci, dacă o grămadă este pară, Alex are strategie sigură de câștig. Altfel, după prima mutare, Paul se va afla în situația de mai sus, așa că Alex va pierde. Iată cum paritățile celor două numere date determină din start câștigătorul

Sursa oficială

#include <bits/stdc++.h>
using namespace std;

int main() {
    int a, b; cin >> a >> b;
    cout << (a % 2 && b % 2 ? 'P' : 'A') << '\n';
    return 0;
}

Cuinelo

• Autor: Iulian Oleniuc
• Dificultate:
• Enunț: CSAcademy

Citeam pe CodeForces niște probleme legate de interclasarea a doi sau mai mulți vectori, și am observat că multe sunt de fapt probleme de programare dinamică. Așa că am încercat să fac și eu una care să combine aceste două concepte. Inițial mi s-a părut că soluția necesită arbori de intervale, chiar persistenți Din păcate a ieșit ceva mult mai ușor, dar totuși elegant. În plus, precalculările necesare l-au cam frustrat pe Bicsi

Avem doi vectori: $a$ de lungime $m$ și $b$ de lungime $n$ Aceștia pot fi interclasați (citiți enunțul pentru clarificare) în foarte multe moduri. Noi trebuie să determinăm numărul maxim de inversiuni pe care le poate avea un vector format prin interclasarea lor.

Soluție

Ideea de bază este simplă: Încercăm să rezolvăm problema în $O(m \cdot n)$ calculând dinamica $\mathrm{dp}_{m \times n}$ Unde $\mathrm{dp}[i][j]$ este numărul maxim de inversiuni pe care le poate avea un vector $c_{ij}$ format prin interclasarea prefixului de lungime $i$ al lui $a$ cu prefixul de lungime $j$ al lui $b$ Cum ultimul element al lui $c_{ij}$ este întotdeauna fie $a_i$ fie $b_j$ obținem recurența

unde $\mathrm{inv}_a[i][j]$ reprezintă numărul de inversiuni care se formează atunci când îl adăugăm pe $a_i$ la $c_{i - 1, j}$ Cu alte cuvinte, câte elemente din $c_{i - 1, j}$ sunt mai mari decât $a_i$ (De remarcat că acest număr nu depinde de ordinea elementelor din $c_{i - 1, j}$ $\mathrm{inv}_b[i][j]$ este definit într-un mod similar. Cele două matrice pot fi precalculate în $O(m \cdot n)$ tot într-o manieră recursivă. Deducerea recurențelor rămâne ca temă pentru cititor.

Sursa oficială

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int m; cin >> m; vector<int> a(m + 1); for (int i = 1; i <= m; i++) cin >> a[i];
    int n; cin >> n; vector<int> b(n + 1); for (int j = 1; j <= n; j++) cin >> b[j];

    vector invA(m + 1, vector<int>(n + 1));
    for (int i = 1; i <= m; i++) {
        for (int k = 1; k < i; k++)
            invA[i][0] += a[k] > a[i];
        for (int j = 1; j <= n; j++)
            invA[i][j] = invA[i][j - 1] + (b[j] > a[i]);
    }

    vector invB(m + 1, vector<int>(n + 1));
    for (int j = 1; j <= n; j++) {
        for (int k = 1; k < j; k++)
            invB[0][j] += b[k] > b[j];
        for (int i = 1; i <= m; i++)
            invB[i][j] = invB[i - 1][j] + (a[i] > b[j]);
    }

    vector dp(m + 1, vector<int>(n + 1));
    for (int i = 1; i <= m; i++) dp[i][0] = dp[i - 1][0] + invA[i][0];
    for (int j = 1; j <= n; j++) dp[0][j] = dp[0][j - 1] + invB[0][j];

    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            dp[i][j] = max(
                dp[i - 1][j] + invA[i][j],
                dp[i][j - 1] + invB[i][j]
            );
    cout << dp[m][n] << '\n';
    return 0;
}

Alex Combines

• Autor: Iulian Oleniuc
• Dificultate:
• Enunț: CSAcademy

Se dă un vector $v$ cu $n$ elemente, numere naturale. Se dau de asemenea $q$ întrebări de forma $(l, r)$ O întrebare $(l, r)$ are semnificația:

Care este numărul minim de subsecvențe continue în care putem partiționa secvența $v[l, r]$ astfel încât să nu existe nicio valoare care să apară de două sau mai multe ori în vreuna dintre aceste subsecvențe?

Această problemă este un exemplu clasic de aplicație la binary lifting, iar faptul că nu ține de arbori o face cu atât mai interesantă. Cu modificări minime, soluția poate fi aplicată la orice problemă de genul ăsta – lucru ilustrat și de template-ul folosit în sursa oficială –, cu condiția ca proprietatea pe care trebuie să o respecte subsecvențele să ne permită să rezolvăm fiecare query într-o manieră greedy.

Soluție

Să vedem mai întâi cum putem rezolva un singur query de forma $(l, r)$ Păi, începem o primă subsecvență de la poziția $l$ și adăugăm elemente până când dăm de unul care apare deja în subsecvența curentă. Când găsim un astfel de element, creăm o nouă subsecvență pornind de la el, și repetăm procesul. Cu alte cuvinte, încercăm să extindem fiecare subsecvență nou creată cât mai mult la dreapta. Strategia este în mod evident corectă – să oprești extinderea subsecvenței curente mai devreme decât e cazul nu poate decât să o „aglomereze” pe următoarea, și, eventual, să o divizeze.

Să formalizăm puțin această idee. Ce ar fi util să calculăm noi pentru fiecare poziție $i$ de la $1$ la $n$ ar fi o funcție $f$ unde $f(i)$ să ne spună care este $j$ul maxim pentru care subsecvența $v[i, j - 1]$ respectă proprietatea din enunț. Valorile lui $f$ se pot calcula foarte ușor în $O(n)$ parcurgând vectorul de la dreapta la stânga și menținând un vector auxiliar $\mathit{last}$ cu semnificație evidentă. Dacă ne gândim puțin, singurul lucru care-l împiedică pe $f(i)$ să fie chiar $f(i + 1)$ este elementul $v[i]$ De aici obținem recurența de mai jos pentru calcularea lui $f$

Acum, răspunsul pentru un query $(l, r)$ poate fi privit drept valoarea minimă $k$ pentru care

relație care se mai scrie

Altfel spus, $k$ este numărul minim de iterații ale lui $f$ pornind din $l$ necesare pentru a atinge o valoare strict mai mare decât $r$ De ce să calculăm această valoare în $O(n)$ când o putem calcula în $O(\log n)$ Aici intervine tehnica de binary lifting. Mai țineți minte Căutarea binară a lui Pătrașcu? Cam aceeași idee se aplică și aici.

Luăm puteri $2^i$ cât mai mari, și încercăm să-l iterăm pe $f$ de $2^i$ ori. Dacă putem, adică dacă noul $f$ este în continuare mai mic sau egal cu $r$ adăugăm la răspuns valoarea $2^i$ Apoi, chiar dacă iterarea a fost efectuată sau nu, încercăm să iterăm funcția de încă $2^{i - 1}$ ori, apoi de $2^{i - 2}$ și tot așa. La final, mai adăugăm $1$ la răspuns, pentru că mai este necesară o iterație pentru a-l depăși pe $r$ Numărul de puteri ale lui $2$ parcurse sunt $[\log_2 (r - l + 1)]$ de unde și complexitatea de $O(\log n)$ per query. Desigur, valorile $f^{(2^i)}(j)$ trebuie precalculate, iar asta se face exact la fel ca la problema Range Minimum Query.

Sursa oficială

#include <bits/stdc++.h>
using namespace std;

class SparseTable {
    vector<vector<int>> dp;

public:
    SparseTable(const vector<int>& fun) :
        dp(log2(fun.size()) + 1, vector<int>(fun.size())) {
        dp[0] = fun;
        for (int i = 1; i < int(dp.size()); i++)
            for (int j = 0; j < int(fun.size()); j++)
                dp[i][j] = dp[i - 1][dp[i - 1][j]];
    }

    int partition(int l, int r) {
        int ans = 1;
        for (int i = dp.size() - 1; i >= 0; i--)
            if (dp[i][l] <= r) {
                l = dp[i][l];
                ans += (1 << i);
            }
        return ans;
    }
};

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int n; cin >> n;
    vector<int> v(n + 1);
    for (int i = 1; i <= n; i++)
        cin >> v[i];

    vector<int> last(1e6 + 1, n + 1);
    vector<int> go(n + 2);
    go[n + 1] = n + 1;
    for (int i = n; i >= 1; i--) {
        go[i] = min(go[i + 1], last[v[i]]);
        last[v[i]] = i;
    }

    SparseTable table(go);
    int q; cin >> q;
    for (int i = 0; i < q; i++) {
        int x, y; cin >> x >> y;
        cout << table.partition(x, y) << '\n';
    }
    return 0;
}

Clown Fiesta

• Autor: Andrei Arhire
• Dificultate:
• Enunț: CSAcademy

Problema asta are enunțul foarte alambicat, pentru că Andrei a încercat cu orice preț să-l formuleze sub forma unui joc, și n-am mai avut timp să-l modificăm. De asta Alex și Paul fac exact aceleași operații, de unde și enunțul a ieșit de două ori mai lung:

If the current position is odd, Alex replaces the current element $a_i$ with $a_i^{a_{i - 1}}$
However, if the current position is even, Paul replaces the current element $a_i$ with $a_i^{a_{i - 1}}$

Prin urmare, vă dau direct enunțul formal: Avem un vector $a$ format din $n$ numere prime. Dându-se un număr prim $m$ strict mai mic decât orice element din $a$ să se calculeze, pentru fiecare $i$ de la $1$ la $n$ valoarea $a_i^{a_{i - 1}^{.^{.^{a_1}}}} \modd m$ Cam mathy problema, dar are o soluție deosebit de elegantă.

Soluție

Mai întâi, voi arăta cum putem calcula $a^b \modd m$ unde $b$ este un număr foarte mare. Sper că este clar că nu putem pur și simplu să-l înlocuim pe $b$ cu $b \modd m$ Nu așa funcționează matematica. În schimb, ne putem folosi de faptul că $m$ este coprim cu toate elementele din $a$ pentru că este prim și diferit de ele. Această condiție ne permite să aplicăm Teorema lui Euler, care ne spune că

unde $a$ și $m$ sunt coprime.

Astfel, observăm că putem reduce drastic valoarea exponentului $b$

Similar, pentru un power-tower de lungime $3$ obținem:

Și tot așa.

Cum noi avem de calculat $n$ expresii de felul ăsta, complexitatea poate să pară a fi $O(n^2 \log n)$ unde $\log$ul vine de la exponențierea logaritmică. Când calculăm un power-tower, avem de calculat $O(n)$ exponenți, ultimul $\modd \varphi(m)$ penultimul $\modd \varphi(\varphi(m))$ și tot așa. Însă, și aici urmează partea interesantă, pentru $m$ul maxim dat, funcția $\varphi$ va ajunge la valoarea $1$ în doar vreo $30$ de pași! Exponentul asociat pasului la care se petrece acest lucru va fi calculat deci modulo $1$ adică va fi $0$ indiferent de ce se află deasupra sa. Așadar, pentru fiecare power-tower, ne interesează doar ultimele cel mult $30$ de exponențieri. În contextul problemei, $30$ este cam $\log_2 m$ de unde complexitatea finală este de ordinul $O(n \log n \log m)$

Sursa oficială

#include <bits/stdc++.h>
using namespace std;

int64_t pwr(int64_t x, int64_t n, int m) {
    if (!n)
        return 1;
    if (n % 2)
        return (x % m) * pwr((x % m) * (x % m) % m, n / 2, m) % m;
    return pwr((x % m) * (x % m) % m, n / 2, m);
}

vector<pair<int, int>> getDiv(int n) {
    vector<pair<int, int>> div;
    for (int d = 2; d * d <= n; d++)
        if (n % d == 0) {
            div.emplace_back(d, 0);
            while (n % d == 0) {
                div.back().second++;
                n /= d;
            }
        }
    if (n > 1)
        div.emplace_back(n, 1);
    return div;
}

int phi(const vector<pair<int, int>>& div) {
    int ans = 1;
    for (auto [p, e] : div) {
        ans *= p - 1;
        for (int i = 1; i < e; i++)
            ans *= p;
    }
    return ans;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m; cin >> n >> m;
    n *= 2;
    vector<int64_t> v(n);
    for (int i = 0; i < n; i++)
        cin >> v[i];

    vector<int> phiItr;
    while (m > 1) {
        phiItr.push_back(m);
        m = phi(getDiv(m));
    }

    function<int64_t(int, int)> fun = [&](int i, int j) -> int64_t {
        if (i == -1)
            return 1;
        if (j >= int(phiItr.size()))
            return 0;
        return pwr(v[i], fun(i - 1, j + 1), phiItr[j]);
    };

    for (int i = 0; i < n; i++)
        cout << fun(i, 0) << ' ';
    cout << '\n';
    return 0;
}

Dr. Anei

• Autor: Andrei Arhire
• Dificultate:
• Enunț: CSAcademy

În această problemă ni se dă un arbore cu portocale (un portocal), având costuri pe noduri, pe care trebuie să efectuăm niște operații. Acestea pot fi de următoarele două tipuri:

1. Update: Se dă o tripletă $(x, y, z)$ Rădăcina arborelui devine $x$ iar dintre fiii lui $x$ îl alegem pe acela al cărui subarbore conține nodul $y$ Valorile tuturor nodurilor din acest subarbore cresc cu $z$ unități.
2. Query: Să se afișeze valoarea nodului $x$

Asta e o problemă foarte bună pentru cei care învață tehnica de liniarizare. Operațiile date ar putea fi executate foarte ușor și eficient pe un vector, adică pe o structură de date liniară. Arborele nu se încadrează în această categorie, așa că o să încercăm noi să-l liniarizăm. Adică, să-l transformăm într-un vector și să stabilim cum anume trebuie să efectuăm operațiile pe acesta, astfel încât noul vector obținut să codifice arborele dorit.

Soluție

Desigur, nu putem sta să reînrădăcinăm arborele la fiecare query, așa că vom fixa rădăcina sa în $1$ și îl vom liniariza. Modul în care facem asta mai exact diferă de la problemă la problemă. În cazul nostru, liniarizarea constă în a face un DFS pe arborele dat în felul următor:

void dfs(int node, int fath) {
    pos[node].push_back(euler.size());
    euler.push_back(node);
    for (int nghb : ad[node])
        if (nghb != fath) {
            dfs(nghb, node);
            pos[node].push_back(euler.size());
            euler.push_back(node);
        }
}

DFS-ul ăsta este bazat pe ideea de parcurgere Euler: De fiecare dată când trecem printr-un nod $x$ atât din tatăl său, cât și dintr-un fiu atunci când urmează să facem DFS din fratele din dreapta al acestuia, adăugăm valoarea lui $x$ la finalul vectorului $\mathrm{euler}$ De asemenea, reținem și un vector de liste $\mathrm{pos}$ unde $\mathrm{pos}_x$ reține pozițiile din $\mathrm{euler}$ la care apare $x$

Iată un exemplu de liniarizare în conformitate cu problema noastră. Doar că în $\mathrm{euler}$ n-am mai folosit costuri, ci am trecut direct nodurile:

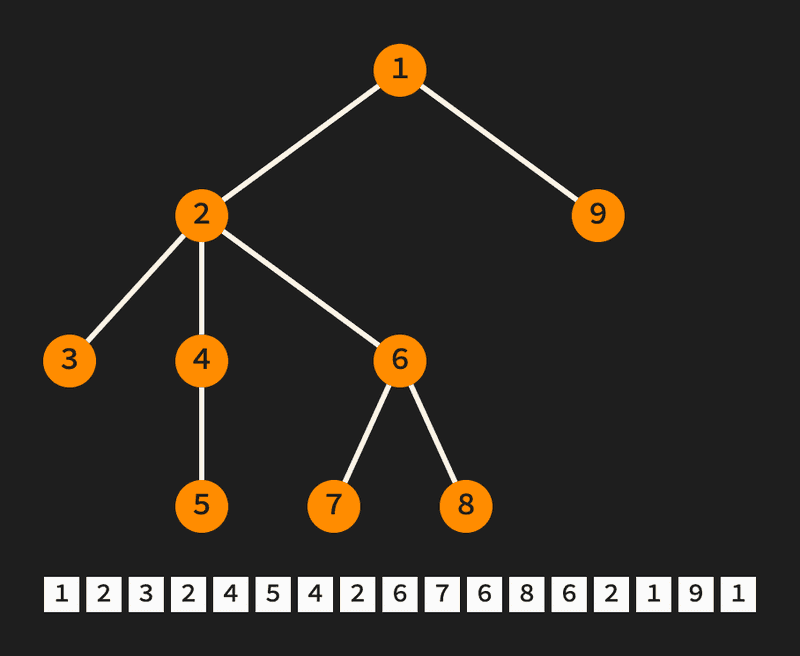
Cum asupra vectorului $\mathrm{euler}$ va trebui să efectuăm update-uri pe intervale, este necesar ca din acesta să construim o structură de date corespunzătoare – fie un arbore de intervale cu lazy update, fie un arbore indexat binar. Eu am ales un AIB, pentru că este mai ușor de implementat și mai rapid.

Query

Pentru operațiile de tip query, trebuie doar să verificăm ce valoare se află în AIB pe una dintre pozițiile pe care se află nodul dat $x$ Desigur, vom alege poziția $\mathrm{pos}_x[0]$

cout << bit.query(pos[x].front()) << '\n';

Update

La operațiile de tip update lucram cu o tripletă de forma $(x, y, z)$ Trebuie să căutăm fiul $u$ al lui $x$ care în versiunea rootată în $x$ a arborelui îl conține pe $y$ În versiunea noastră a arborelui, rootată în $1$ acest $u$ este fie un fiu al lui $x$ fie tatăl lui $x$

O observație importantă despre liniarizare: Nodurile dintre două apariții consecutive ale lui $x$ determină un subarbore al lui $x$ Asta înseamnă că, dacă $u$ este un fiu al lui $x$ atunci pur și simplu dăm update pe intervalul $(l, r)$ Unde $l$ și $r$ sunt pozițiile aparițiilor lui $x$ care determină o subsecvență de lungime minimă ce include toate aparițiile lui $y$ Cum listele din $\mathrm{pos}$ sunt în mod intrinsec sortate crescător, putem căuta binar aceste poziții.

if (pos[x].front() < pos[y].front() && pos[y].back() < pos[x].back()) {
    const int l = lower_bound(pos[x].begin(), pos[x].end(), pos[y].front()) - pos[x].begin() - 1;
    const int r = lower_bound(pos[x].begin(), pos[x].end(), pos[y].front()) - pos[x].begin();
    bit.update(pos[x][l] + 1, pos[x][r] - 1, z);
}

Probabil am folosit cam multe cuvinte, dar dacă veți face singuri niște exemple folosind poza de mai sus, sunt sigur că o să înțelegeți perfect care e treaba.

Mai avem un caz, dat de ramura else a if-ului precedent, cel în care $u$ este tatăl lui $x$ În acest caz, dăm update la toate nodurile aflate în exteriorul subarborelui cu rădăcina în $x$

else {
    bit.update(0, pos[x].front() - 1, z);
    bit.update(pos[x].back() + 1, 2 * n - 2, z);
}

Complexitate finală: $O((n + q) \log n)$

Sursa oficială

#include <bits/stdc++.h>
using namespace std;

class FenTree {
    int n;
    vector<int64_t> bit;

public:
    FenTree(int n) :
        n(n), bit(n + 1) { }

    void update(int left, int right, int val) {
        if (left <= right) {
            for (int i = left + 1; i <= n; i += i & -i)
                bit[i] += val;
            for (int i = right + 2; i <= n; i += i & -i)
                bit[i] -= val;
        }
    }

    int64_t query(int pos) {
        int64_t sum = 0;
        for (int i = pos + 1; i >= 1; i -= i & -i)
            sum += bit[i];
        return sum;
    }
};

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, q; cin >> n >> q;
    vector<int> cost(n + 1);
    for (int i = 1; i <= n; i++)
        cin >> cost[i];
    vector<vector<int>> ad(n + 1);
    for (int i = 1; i < n; i++) {
        int x, y; cin >> x >> y;
        ad[x].push_back(y);
        ad[y].push_back(x);
    }

    vector<int> euler;
    vector<vector<int>> pos(n + 1);
    function<void(int, int)> dfs = [&](int node, int fath) {
        pos[node].push_back(euler.size());
        euler.push_back(node);
        for (int nghb : ad[node])
            if (nghb != fath) {
                dfs(nghb, node);
                pos[node].push_back(euler.size());
                euler.push_back(node);
            }
    };
    dfs(1, 0);
    FenTree bit(2 * n - 1);
    for (int i = 0; i < 2 * n - 1; i++)
        bit.update(i, i, cost[euler[i]]);

    for (int i = 0; i < q; i++) {
        int t; cin >> t;
        if (t == 1) {
            int x, y, z; cin >> x >> y >> z;
            if (pos[x].front() < pos[y].front() && pos[y].back() < pos[x].back()) {
                const int l = lower_bound(pos[x].begin(), pos[x].end(), pos[y].front()) - pos[x].begin() - 1;
                const int r = lower_bound(pos[x].begin(), pos[x].end(), pos[y].front()) - pos[x].begin();
                bit.update(pos[x][l] + 1, pos[x][r] - 1, z);
            }
            else {
                bit.update(0, pos[x].front() - 1, z);
                bit.update(pos[x].back() + 1, 2 * n - 2, z);
            }
        }
        else {
            int x; cin >> x;
            cout << bit.query(pos[x].front()) << '\n';
        }
    }
    return 0;
}

Etianap

• Autor: Răzvan Panaite
• Dificultate:
• Enunț: CSAcademy

Problema asta a fost scrisă cu un an înainte de FIICode. Răzvan a zis să facă și el o problemă pentru PbInfo, asta după ce l-am inspirat eu cu problemele mele de doi bani: Sierpinski și Secv011. Însă problema n-a mai fost făcută publică niciodată, pentru că admin-ul PbInfo n-a fost mulțumit de calitatea enunțului. A zis că intervalele (mulțimi continue) ar trebui să fie înlocuite de secvențe (mulțimi discrete).

Răzvan n-a mai avut chef să facă acest replace, și iată-ne peste un an la FIICode cu o problemă bombă. Și cu un enunț pe măsură. Am murit când l-am tradus în engleză și mi-am dat seama că meșterul-zidar Paftenie s-a transformat într-un lider mason (master-mason)

Avem un vector $v$ format din $n$ numere naturale și trebuie să răspundem la $q$ întrebări de forma $(x, y, z)$ cu semnificația:

Câte dintre elementele $v[x], v[x + 1], \ldots, v[y]$ sunt coprime cu $z$

Soluție

Fiind o problemă care conține cuvintele câte și coprime, este foarte posibil să avem nevoie de principiul includerii și excluderii. Având un set de numere naturale și o valoare $a$ putem număra foarte ușor câte dintre acestea sunt coprime cu $a$ astfel: Mai întâi, inițializăm răspunsul cu dimensiunea acestui set. Apoi, ne uităm la divizorii primi ai lui $a$ $p_1, p_2, \ldots, p_k$

Este clar că din răspuns trebuie să scădem numărul multiplilor lui $p_1$ Dar și ai lui $p_2$ $p_3$ etc. Însă acum avem o problemă – am scăzut de mai multe ori numerele divizibile cu cel puțin două $p$uri, așa că trebuie adunați la loc. După care trebuie să scădem numerele divizibile cu cel puțin trei $p$uri și așa mai departe.

Pentru un număr fixat, partea de includere și excludere presupune să generăm toate submulțimilor de divizori primi ai acestui număr. (Pe parcurs, menținem produsul elementelor din submulțimea curentă, precum și numărul lor.) Putem face asta folosind fie backtracking, fie dinamică pe biți. Numerele din $v$ pot avea cel mult $8$ factori primi, așa că ambele metode au complexitatea $O(2^8)$

Vom răspunde la query-uri offline (le procesăm simultan pe toate), folosind o tehnică numită baleiere. În acest scop, transformăm fiecare query $i$ de forma $(x, y, z)$ în două evenimente de forma $(x - 1, -i)$ și $(y, +i)$ semnificând faptul că imediat după poziția $x - 1$ „începe” query-ul $i$ iar imediat după poziția $y$ „se termină” query-ul $i$ După ce terminăm de creat aceste evenimente, începem să parcurgem vectorul dat de la stânga la dreapta, menținând un vector de frecvență pentru numerele ce urmează a fi generate prin backtracking.

La fiecare pas $i$ actualizăm vectorul $\mathrm{frq}$ aplicând PINEX pe $v[i]$ după care baleiem evenimentele din $\mathrm{qry}$ actualizând răspunsurile necesare: Ne uităm la $z$ul corespunzător query-ului curent și facem PINEX pe acesta. Apoi, dacă indexul de query $i$ este negativ, adică query-ul $-i$ tocmai începe, scădem din $\mathrm{ans}[i]$ valorile din $\mathrm{frq}$ de pe pozițiile ce rezultă din PINEX. Altfel, dacă $i$ este pozitiv, adică query-ul $+i$ se termină, adunăm la $\mathrm{ans}[i]$ valorile respective. Asta înseamnă că am adunat și ce a rezultat din prefixul $x - 1$ dar este OK din moment ce am scăzut mai devreme aceste valori. Exact ca la sume parțiale.

Complexitatea finală este $O(n \cdot 2^8)$ Recomand să vă uitați cu atenție peste sursa oficială, ca să remarcați cât de utilă este o funcție de genul factorizationAndBkt cu callback (funcție transmisă ca parametru) în acest context.

Sursa oficială

#include <bits/stdc++.h>
using namespace std;

class Sieve {
    vector<bool> sieve;
    vector<int> primes;

public:
    Sieve(int n) : sieve(n + 1) {
        sieve[0] = sieve[1] = true;
        for (int i = 2; i * i <= n; i++)
            if (!sieve[i])
                for (int j = i * i; j <= n; j += i)
                    sieve[j] = true;
        for (int i = 2; i <= n; i++)
            if (!sieve[i])
                primes.push_back(i);
    }

    auto begin() { return primes.begin(); }
    auto end() { return primes.end(); }
};

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int n; cin >> n;
    vector<int> arr(n + 1);
    for (int i = 1; i <= n; i++)
        cin >> arr[i];

    int q; cin >> q;
    vector<int> ans(q + 1);
    vector<vector<pair<int, int>>> qry(n + 1);
    for (int i = 1; i <= q; i++) {
        int x, y, z; cin >> x >> y >> z;
        qry[x - 1].emplace_back(z, -i);
        qry[y].emplace_back(z, +i);
        ans[i] = y - x + 1;
    }

    Sieve sieve(1e3);
    auto factorizationAndBkt = [&](int num, function<void(int, int)> callback) {
        vector<int> div;
        for (int d : sieve) {
            if (d * d > num)
                break;
            if (num % d == 0) {
                div.push_back(d);
                while (num % d == 0)
                    num /= d;
            }
        }
        if (num > 1)
            div.push_back(num);
        function<void(int, int, int)> bkt = [&](int pos, int prod, int cnt) {
            if (pos == int(div.size())) {
                if (prod > 1)
                    callback(prod, cnt);
                return;
            }
            bkt(pos + 1, prod, cnt);
            bkt(pos + 1, prod * div[pos], cnt + 1);
        };
        bkt(0, 1, 0);
    };

    vector<int> frq(1e6 + 1);
    for (int i = 1; i <= n; i++) {
        factorizationAndBkt(arr[i], [&](int prod, int cnt) {
            frq[prod] += (cnt % 2 ? +1 : -1);
        });
        for (auto it : qry[i])
            factorizationAndBkt(it.first, [&](int prod, int) {
                if (it.second < 0)
                    ans[-it.second] += frq[prod];
                else
                    ans[+it.second] -= frq[prod];
            });
    }
    for (int i = 1; i <= q; i++)
        cout << ans[i] << '\n';
    return 0;
}

Cam atât despre FIICode 2021. Dacă vă numărați printre premianți, sper că v-au plăcut diplomele făcute de mine Îmi pare rău că au fost printate cu tot cu marginile alea albe, dar asta e. Ne vedem data viitoare cu o nouă ediție a concursului care și-a făcut un renume din a readuce la viață platforma CSAcademy o dată pe an! Și promit că am terminat cu articolele pe care nu le așteaptă nimeni.