Trie în C++. Problema Xor Max de pe InfoArena

de Iulian Oleniuc | 06/02/2021 | Algoritmică și structuri de date

În acest articol voi prezenta structura de date numită trie, precum și câteva aplicații interesante ale acesteia. Tria este o structură de date arborescentă, ușor de implementat, folosită pentru a stoca un set de cuvinte într-o manieră compactă. Din acest motiv, putem spune că tria este o structură de date de tip dicționar. Avantajul principal al acesteia este complexitatea căutării unui cuvânt, care este liniară în lungimea sa, nedepinzând de mărimea dicționarului. De aici și numele structurii (trie provine de la retrieval).

Structura unei trie

Vom nota cu $\Sigma$ lungimea alfabetului cu care lucrăm, de obicei $26$ (de la alfabetul englez). O trie este un arbore în care fiecare nod are maxim $\Sigma$ fii, câte unul pentru fiecare literă din alfabet. Cuvintele stocate în trie pot fi obținute prin citirea caracterelor aflate pe lanțul de la rădăcină la diverse noduri, numite frunze. Iată mai jos o trie construită pe baza cuvintelor $\texttt{lac}$ $\texttt{lat}$ $\texttt{latin}$ $\texttt{lung}$ $\texttt{mare}$ etc. Nodurile frunză sunt marcate cu verde.

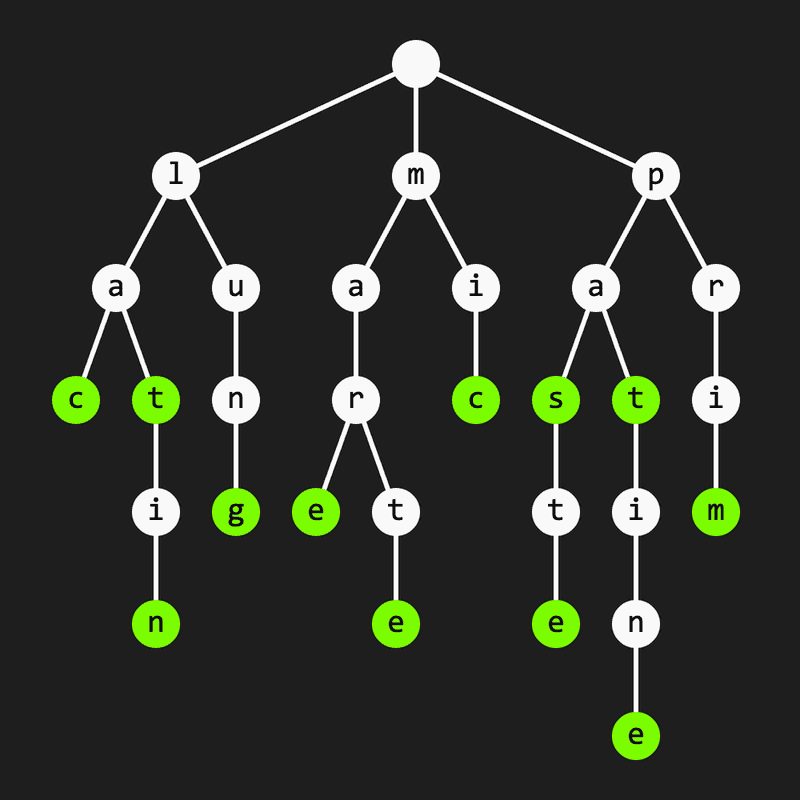
Am ales să pun literele în noduri pentru a desena mai ușor tria, însă conceptual este mai bine să vă gândiți că literele sunt asociate muchiilor. În acest mod, nu mai este nevoie să-i asociem rădăcinii caracterul nul. De remarcat că un nod nu poate avea doi fii corespunzători aceleiași litere.

Implementare în C++

În continuare, vom scrie o clasă Trie în C++, pentru rezolvarea problemei cu același nume de pe InfoArena. Această problemă ne cere să implementăm eficient operațiile de inserare, căutare, ștergere și LCP (longest common prefix). Mai întâi ne vom axa pe implementarea clasică, cu pointeri și funcții recursive, după care vă voi arăta și o variantă oarecum mai simplă, dar cu un mic dezavantaj în ceea ce privește memoria.

Deocamdată, clasa Trie are nevoie de doi membri privați: cnt (numărul de cuvinte care se termină în nodul curent) și un vector de pointeri next, de lungime $\Sigma$ unde next[i] ne spune în ce nod ne ducem dacă urmăm legătura corespunzătoare celei de-a i-a litere din alfabet. Dacă next[i] este nullptr, înseamnă că nu există tranziție către litera i.

class Trie {
    int cnt = 0;
    Trie *next[26] = {};
};

Funcția `insert`

Această funcție, la fel ca și următoarele, primește ca parametri un string str și poziția curentă din acesta (pos). Funcția insert inserează recursiv cuvântul str în trie, astfel: Dacă poziția curentă este egală cu lungimea string-ului, înseamnă că ne-am terminat treaba, așa că incrementăm cnt-ul din nodul curent și ne oprim. Altfel, urmăm muchia către litera curentă (str[pos] - 'a'), și continuăm inserarea din nodul următor, începând cu poziția pos + 1. Înainte de asta, avem grijă să creăm nodul next[str[pos] - 'a'], în caz că acesta nu există deja.

void insert(const string& str, int pos = 0) {
    if (pos == int(str.size()))
        cnt++;
    else {
        if (!next[str[pos] - 'a'])
            next[str[pos] - 'a'] = new Trie;
        next[str[pos] - 'a']->insert(str, pos + 1);
    }
}

Iată o super-animație marca InfoGenius, care arată cum este construită tria de mai sus prin inserări succesive:

Funcția `count`

Funcția count returnează numărul de apariții ale cuvântului str în trie. Pentru a face asta, trebuie ca mai întâi să ajungem în nodul în care se termină cuvântul dat, iar apoi să returnăm cnt-ul din acesta. Așadar, funcția count va semăna foarte mult cu insert, numai că aici, dacă nu există tranziție din nodul curent către litera următoare, returnăm 0 și ne oprim, deoarece str nu se găsește în trie.

int count(const string& str, int pos = 0) {
    if (pos == int(str.size()))
        return cnt;
    if (!next[str[pos] - 'a'])
        return 0;
    return next[str[pos] - 'a']->count(str, pos + 1);
}

Funcția `lcp`

Funcția lcp trebuie să returneze lungimea celui mai lung prefix comun al lui str cu un cuvânt oarecare din trie. Deja ar trebui să fie clar cum facem asta: Coborâm în trie până când fie ne blocăm într-un nod fără tranziție către următoarea literă, fie ajungem la finalul string-ului. Ce returnăm de fapt este lungimea lanțului de la rădăcină până la nodul în care ne oprim.

int lcp(const string& str, int pos = 0) {
    if (pos == int(str.size()))
        return 0;
    if (!next[str[pos] - 'a'])
        return 0;
    return 1 + next[str[pos] - 'a']->lcp(str, pos + 1);
}

Funcția `erase`

Funcția erase trebuie să șteargă din trie o apariție a cuvântului str. (Ni se garantează că str apare cel puțin o dată în trie înainte să-i dăm erase.) Avem două cazuri – fie putem șterge nodul node în care se termină str, fie nu. Pentru ca node să poată fi șters, trebuie ca numărul de cuvinte care se termină în subarborele cu rădăcina în acesta să fie exact 1, adică doar cel pe care vrem să-l ștergem. De exemplu, în tria de mai jos nu putem șterge nodul în care se termină cuvântul $\texttt{lat}$ pentru că „sub el” se află frunza corespunzătoare lui $\texttt{latin}$ Altfel spus, $\texttt{lat}$ este un prefix al lui $\texttt{latin}$

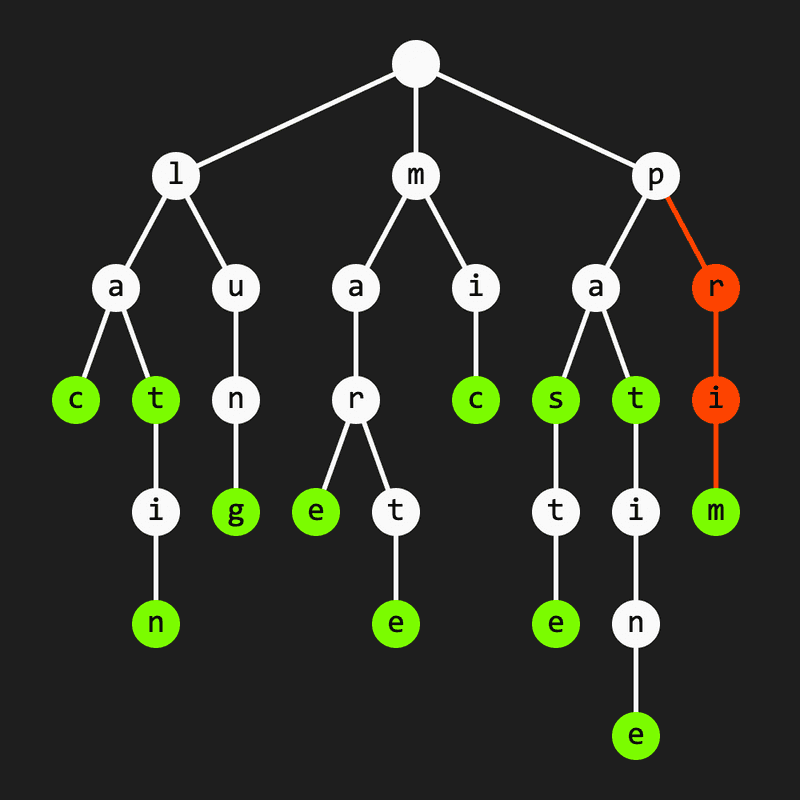
În schimb, putem șterge nodul în care se termină $\texttt{prim}$ De fapt, putem șterge și din strămoșii lui $\texttt{prim}$ mai exact pe $\texttt{pri}$ și pe $\texttt{pr}$ Nodul $\texttt{p}$ nu poate fi șters, deoarece este prefix al mai multor cuvinte stocate în trie, nu doar al lui $\texttt{prim}$

Haideți să mai adăugăm un membru privat la clasa Trie, notat cu lvs (de la leaves), care să reprezinte suma valorilor cnt ale nodurilor din subarborele nodului curent. Această valoare poate fi menținută fără mari bătăi de cap, incrementând-o când vizităm nodul curent în cadrul unei inserări și decrementând-o când efectuăm o ștergere.

Acum că avem calculată această informație, ne este mai ușor să rezumăm ce trebuie să facem concret în funcția erase: Coborâm în trie până în nodul în care se termină str, decrementând valorile lvs întâlnite pe parcurs. După ce ajungm în node, îl decrementăm pe cnt și ne întoarcem în rădăcină pe același traseu, ștergând nodurile al căror lvs a devenit 0.

void erase(const string& str, int pos = 0) {
    lvs--;
    if (pos == int(str.size()))
        cnt--;
    else {
        next[str[pos] - 'a']->erase(str, pos + 1);
        if (!next[str[pos] - 'a']->lvs) {
            delete next[str[pos] - 'a'];
            next[str[pos] - 'a'] = nullptr;
        }
    }
}

Sursa completă

Iată cum arată sursa completă pentru problema Trie:

Trie
#include <bits/stdc++.h>
using namespace std;

ifstream fin("trie.in");
ofstream fout("trie.out");

class Trie {
    int cnt = 0;
    int lvs = 0;
    Trie *next[26] = {};

public:
    void insert(const string& str, int pos = 0) {
        lvs++;
        if (pos == int(str.size()))
            cnt++;
        else {
            if (!next[str[pos] - 'a'])
                next[str[pos] - 'a'] = new Trie;
            next[str[pos] - 'a']->insert(str, pos + 1);
        }
    }

    void erase(const string& str, int pos = 0) {
        lvs--;
        if (pos == int(str.size()))
            cnt--;
        else {
            next[str[pos] - 'a']->erase(str, pos + 1);
            if (!next[str[pos] - 'a']->lvs) {
                delete next[str[pos] - 'a'];
                next[str[pos] - 'a'] = nullptr;
            }
        }
    }

    int count(const string& str, int pos = 0) {
        if (pos == int(str.size()))
            return cnt;
        if (!next[str[pos] - 'a'])
            return 0;
        return next[str[pos] - 'a']->count(str, pos + 1);
    }

    int lcp(const string& str, int pos = 0) {
        if (pos == int(str.size()))
            return 0;
        if (!next[str[pos] - 'a'])
            return 0;
        return 1 + next[str[pos] - 'a']->lcp(str, pos + 1);
    }
};

int main() {
    Trie trie;
    int type; string str;
    while (fin >> type >> str)
        if (!type)
            trie.insert(str);
        else if (type == 1)
            trie.erase(str);
        else if (type == 2)
            fout << trie.count(str) << '\n';
        else
            fout << trie.lcp(str) << '\n';
    return 0;
}

Implementare alternativă

Iată și o implementare mai puțin populară, în care funcțiile sunt implementate iterativ. Aici, nodurile sunt ținute într-un vector alocat dinamic, iar pointerii sunt de fapt indici în acest vector. Dezavantajul este că această metodă de stocare a nodurilor nu ne permite să eliberăm efectiv memorie în urma unui erase. Nodurile sunt eliminate doar conceptual, prin ștergerea muchiei către primul nod dintre rădăcină și node care are lvs-ul 0.

Trie
#include <bits/stdc++.h>
using namespace std;

ifstream fin("trie.in");
ofstream fout("trie.out");

class Trie {
    struct Node {
        int cnt = 0;
        int lvs = 0;
        int next[26] = {};
    };
    vector<Node> trie{1};

public:
    void insert(const string& str) {
        int node = 0;
        for (char chr : str) {
            if (!trie[node].next[chr - 'a']) {
                trie[node].next[chr - 'a'] = trie.size();
                trie.emplace_back();
            }
            node = trie[node].next[chr - 'a'];
            trie[node].lvs++;
        }
        trie[node].cnt++;
    }

    void erase(const string& str) {
        int node = 0;
        for (char chr : str) {
            node = trie[node].next[chr - 'a'];
            trie[node].lvs--;
        }
        trie[node].cnt--;
        node = 0;
        for (char chr : str) {
            if (!trie[trie[node].next[chr - 'a']].lvs) {
                trie[node].next[chr - 'a'] = 0;
                return;
            }
            node = trie[node].next[chr - 'a'];
        }
    }

    int count(const string& str) {
        int node = 0;
        for (char chr : str) {
            if (!trie[node].next[chr - 'a'])
                return 0;
            node = trie[node].next[chr - 'a'];
        }
        return trie[node].cnt;
    }

    int lcp(const string& str) {
        int node = 0, len = 0;
        for (char chr : str) {
            if (!trie[node].next[chr - 'a'])
                return len;
            node = trie[node].next[chr - 'a'];
            len++;
        }
        return len;
    }
};

int main() {
    Trie trie;
    int type; string str;
    while (fin >> type >> str)
        if (!type)
            trie.insert(str);
        else if (type == 1)
            trie.erase(str);
        else if (type == 2)
            fout << trie.count(str) << '\n';
        else
            fout << trie.lcp(str) << '\n';
    return 0;
}

Totuși, în majoritatea problemelor interesante de la concursuri, avem nevoie doar de funcția insert (și poate count), restul problemei reducându-se la o dinamică pe arbore sau ceva. Iar în acest caz, implementarea asta mi se pare ceva mai simplă.

Complexitate

În cazul ambelor implementări, funcția insert (la fel ca și celelalte trei de mai sus) are complexitatea $O(n)$ unde $n$ este lungimea string-ului dat. Partea mai puțin bună este consumul relativ mare de memorie – pentru fiecare nod reținem $\Sigma$ pointeri/ indici, dintre care majoritatea nu sunt folosiți. Iar asta se reflectă în complexitatea unui DFS, care ar avea constanta $\Sigma$ Putem reduce această constantă la $1$ înlocuind vectorul next cu un map. Însă, dacă facem asta, complexitatea lui insert devine $O(n \log \Sigma)$ Depinde de problemă dacă este mai bine să folosim map sau nu.

Cât despre numărul de noduri ale unei trie, în cel mai rău caz acesta poate fi $O(s)$ unde $s$ este suma lungimilor cuvintelor din trie. Acest caz se poate atinge, de exemplu, când toate cuvintele încep cu altă literă. Dacă avem mai multe cuvinte decât litere în alfabet, putem spune că cel mai rău caz se atinge atunci când perechile formate din primele două litere din fiecare cuvânt sunt diferite. Dacă tot avem prea puține litere, ne putem uita la primele trei litere din fiecare cuvânt, și tot așa. Complexitatea în spațiu rămâne $O(s)$

Aplicații clasice

Sortarea unei liste de cuvinte. Construim o trie din cuvintele date, reținând în fiecare frunză o listă cu indicii cuvintelor care se termină în nodul respectiv. Apoi, efectuăm o parcurgere preordine a triei, afișând indicii întâlniți pe parcurs. Putem adapta algoritmul și pentru sortarea unui vector de întregi, inserând în trie reprezentările lor în baza $2$ Chiar am obține o complexitate bună: $O(n \log n)$ Însă, din cauza consumului mare de memorie auxiliară și a faptului că aceasta nu este o sortare prin comparare, nu veți auzi prea des de ea.
Funcția de autocomplete. Aici mă refer la căutarea de cuvinte cu un prefix dat, adică ceea ce face Google când vă oferă sugestii de căutare. Navigăm în trie până la nodul în care se termină prefixul acela, după care enumerăm frunzele din subarborele acelui nod.
Cel mai lung prefix comun a două cuvinte. Să zicem că avem dat un set de cuvinte și trebuie să răspundem la multe întrebări de forma „Care este lungimea LCP-ului cuvintelor $x$ și $y$ Mai întâi, construim tria formată din cuvintele date. Apoi, problema se reduce la a determina adâncimea LCA-ului nodurilor în care se termină $x$ și respectiv $y$ Puteți citi despre LCA aici.

De asemenea, tria este esențială în algoritmul Aho-Corasick, care rezolvă următoarea problemă: „Dându-se un string $s$ și un dicționar $t$ să se determine, pentru fiecare cuvânt $x \in t$ numărul său de apariții în șirul $s$ În plus, tria stă la baza a două structuri de date mai avansate, Suffix Tree și Suffix Automata, care ne ajută să rezolvăm în timp liniar probleme de genul: „Care este cea mai lungă subsecvență comună string-urilor $s_1, s_2, \ldots, s_n$

Problema Xor Max de pe InfoArena

În această problemă ni se dă un vector $a$ de $n$ numere naturale, iar noi trebuie să determinăm o subsecvență a sa cu suma xor maximă. Suma xor a unei subsecvențe $[i, j]$ este $a_i \oplus a_{i + 1} \oplus \cdots \oplus a_j$ unde $\oplus$ reprezintă desigur operația xor. În caz că există mai multe soluții, se va alege secvența cu $j$ ul minim. Dacă în continuare există mai multe soluții, se va alege secvența de lungime minimă.

Dacă $\oplus$ era $+$
Să ne gândim mai întâi cum rezolvam problema dacă suma xor era de fapt sumă normală. Mă refer la soluția cu sume parțiale. Păi, calculăm sumele parțiale ale vectorului dat, iar când am ajuns la o poziție $j$ ne uităm în stânga sa după o poziție $i$ astfel încât valoarea $\mathrm{ps}[j] - \mathrm{ps}[i]$ să fie maximă. Cum $j$ este fixat, vom obține diferența maximă atunci când $\mathrm{ps}[i]$ este minim. Pentru a accesa această valoare în timp constant, este de ajuns să menținem minimul sumelor parțiale calculate până la pasul curent.

Cum $x \oplus x = 0, \forall x \in \mathbb{N}$ putem folosi tehnica sumelor parțiale și în cazul operației xor. Adică,

a_{i + 1} \oplus a_{i + 2} \oplus \cdots \oplus a_j = \mathrm{ps}[j] \oplus \mathrm{ps}[i]

Acum, trebuie să vedem ce presupune să găsim cel mai bun indice $i$ pentru un capăt dreapta fixat $j$ Ne uităm la biții lui $\mathrm{ps}[j]$ Dacă cel mai semnificativ bit al său este $x$ atunci vom alege, dacă se poate, ca primul bit al lui $\mathrm{ps}[i]$ să fie $\neg x$ deoarece $x \oplus \neg x = 1$ iar asta clar ne garantează o sumă mai mare decât dacă am alege ca bitul curent să fie $x$ căci $x \oplus x = 0$ Apoi, trecem la al doilea cel mai semnificativ bit, $y$ iar dintre candidații de la pasul precedent îi vom da la o parte, dacă putem, pe cei cu al doilea bit egal cu $y$ Și așa mai departe.

Exemplu

Acest algoritm se pretează perfect pe o trie. Mai exact, o trie în care reținem reprezentările binare ale sumelor xor parțiale calculate până la pasul curent. (Bine, de fiecare dată când inserăm o sumă nouă în tria asta, va trebui ca după ultimul bit să punem și poziția din vector a sumei respective.) Spre exemplu, dacă tria curentă este cea de mai jos și $\mathrm{ps}[j] = 11000100_{(2)}$ atunci vom alege $i = 5$

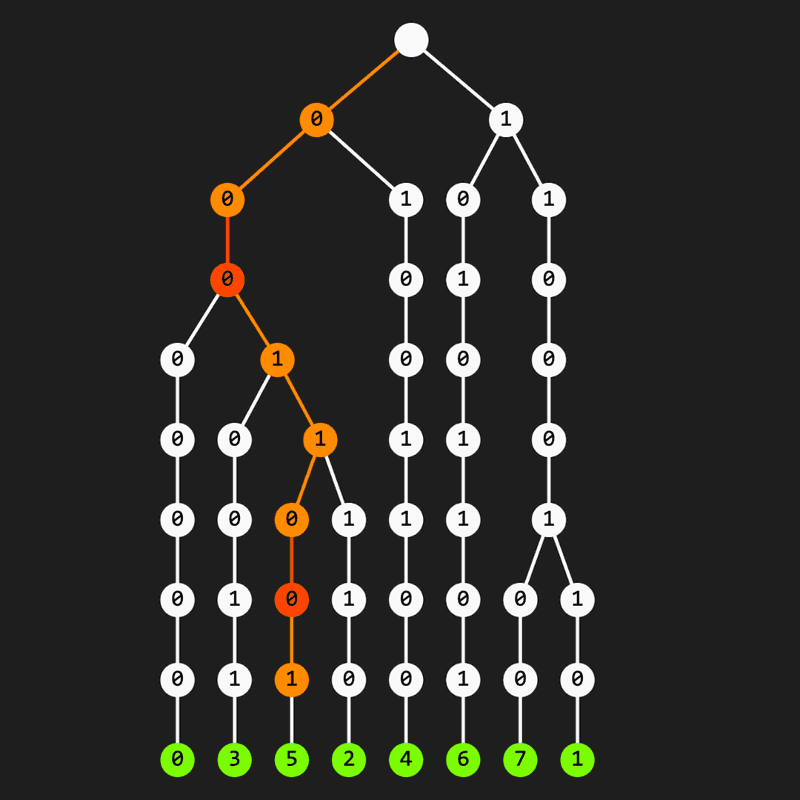
Am colorat cu portocaliu nodurile în care am ajuns alegând valoarea $\neg x$ și cu roșu cele unde n-am putut alege decât $x$ – valoarea bitului curent din suma dată. De remarcat faptul că suma $\mathrm{ps}[0]$ este prin definiție egală cu $0$ și va apărea întotdeauna în trie.

Sursă C++

Iată mai jos o sursă de 100 de puncte la problema Xor Max. Complexitatea finală a algoritmului este de ordinul $O(n \log n)$ unde $\log$ ul vine de la numărul de biți ai unui număr, care este totodată înălțimea triei.

Problema Xor Max
#include <bits/stdc++.h>
using namespace std;

ifstream fin("xormax.in");
ofstream fout("xormax.out");

class Trie {
    struct Node {
        int pos = 0;
        int next[2] = {};
    };
    vector<Node> trie{1};

public:
    void insert(int pos, int val) {
        int node = 0;
        for (int bit = 20; bit >= 0; bit--) {
            bool now = (val & (1 << bit));
            if (!trie[node].next[now]) {
                trie[node].next[now] = trie.size();
                trie.emplace_back();
            }
            node = trie[node].next[now];
        }
        trie[node].pos = pos;
    }

    tuple<int, int, int> query(int pos, int val) {
        int node = 0, ans = 0;
        for (int bit = 20; bit >= 0; bit--) {
            bool now = (val & (1 << bit));
            if (!trie[node].next[!now])
                node = trie[node].next[now];
            else {
                node = trie[node].next[!now];
                ans |= (1 << bit);
            }
        }
        return make_tuple(ans, -pos, trie[node].pos + 1);
    }
};

int main() {
    Trie trie; trie.insert(0, 0);
    int n; fin >> n;
    tuple<int, int, int> ans(-1, 0, 0);
    for (int i = 1, sum = 0; i <= n; i++) {
        int x; fin >> x; sum ^= x;
        ans = max(ans, trie.query(i, sum));
        trie.insert(i, sum);
    }
    fout << get<0>(ans) << ' ' << get<2>(ans) << ' ' << -get<1>(ans) << '\n';
    return 0;
}