
Admitere Informatică Iași 2018 – Subiecte și rezolvări
Recent, a fost dată admiterea la Facultatea de Informatică din Iași. Puteți găsi subiectele din 2018 aici, iar baremul aici. Cum baremul nu oferă soluții complete ale problemelor, în acest articol voi prezenta rezolvările subiectelor date la admitere.
Subiectul I. Problema 1.
Variabilele memorează valori întregi astfel încât și Precizați care dintre expresiile C++ de mai jos, atunci când este adevărată, implică faptul că intersecția intervalelor și este nevidă.
(u > t) && (v > z)!((u > t) || (v > z))(u <= t) && (v == z)!((u > t) || (t > u))
Simplificând un pic expresiile de mai sus, folosind legile lui De Morgan (la B și D), obținem:
u > t && v > zu <= t && v <= zu <= t && v == zu <= t && t <= u
Prima expresie implică faptul că începutul primului interval este strict mai mare decât sfârșitul celui de-al doilea. Asta înseamnă că intersecția intervalelor este mulțimea vidă. A doua expresie nu este suficient de bună; un contraexemplu este A treia expresie nu funcționează niciodată, pentru că primul interval este deschis în dreapta, iar al doilea deschis în stânga. Chiar dacă intersecția lor este vidă. Ultima expresie implică faptul că și sunt egale, și cum primul interval îl conține pe și al doilea îl conține pe intersecția celor două intervale are cardinalul și deci nenul. Prin urmare, răspunsul corect este D.
Subiectul I. Problema 2.
Se consideră subprogramul de mai jos, descris în pseudocod. Subprogramul primește două numere naturale nenule prin parametrii și și întoarce un număr natural când se oprește.
a) Care este valoarea returnată de subprogram pentru parametrii și
Iată valorile variabilelor după fiecare intrare în while:
Așadar, valoarea returnată de funcție este
b) Care este cel mai mare număr prim astfel încât să returneze
Dacă ne mai dăm niște exemple, se observă că funcția aceasta calculează produsul dintre parametrii săi. În timp logaritmic față de chiar. Cum descompunerea în factori primi a lui este răspunsul este
c) Înlocuiți instrucțiunea
x <- x / 2cu o secvență de pseudocod echivalentă și care folosește ca operații aritmetice doar adunări sau scăderi repetate.
Trebuie să efectuăm o împărțire folosind o instrucțiune repetitivă. Ei bine, se știe că împărțirea este o scădere repetată. Mai exact, se obține scăzând din valoarea cât timp este mai mare sau egal cu câtul împărțirii va fi dat de numărul de pași efectuați. Iată secvența de pseudocod cerută:
cnt <- 0cât timp x >= 2 x <- x - 2 cnt <- cnt + 1x <- cntd) Scrieți o funcție C++ care implementează subprogramul dat.
Trebuie doar să traducem pseudocodul în C++. Iată funcția scrisă în C++:
int F(int x, int y) { int acc = 0; while (x) { if (x % 2) acc += y; x /= 2; y *= 2; } return acc;}Subiectul II. Problema 1.
Fie mulțimea tuturor secvențelor de lungime formate doar din cifrele și Graful neorientat are drept vârfuri elementele lui și muchii doar între vârfuri reprezentând secvențe care diferă exact într-una dintre cele poziții. Care este numărul total de muchii din
Asta e o problemă destul de interesantă; nu are soluția chiar imediată. În primul rând, numărul de noduri ale grafului, adică numărul de secvențe binare de lungime este Numărul de vecini ai fiecărui nod este pentru că cele două extremități ale unei muchii pot diferi prin bitul de pe orice poziție cuprinsă între și Dar graful este neorientat, așa că trebuie să numărăm muchiile astfel încât să nu se repete.
Putem, de exemplu, ca pentru fiecare nod să numărăm doar vecinii săi mai mari lexicografic decât el. Un vecin este mai mare lexicografic dacă și numai dacă se obține prin înlocuirea unui bit cu bitul Deci, numărul de muchii pe care le numărăm pentru nodul respectiv este egal numărul de biți ai lui. Prin urmare, răspunsul problemei este egal cu numărul de biți din scrierea tuturor nodurilor. Acesta este egal cu jumătate din numărul total de biți, pentru că jumătate dintre noduri au valoarea pe o anumită poziție, iar restul au Cum varianta corectă este B.
Subiectul II. Problema 2.
Un graf este colorabil dacă este cel mai mic număr pentru care putem colora (eticheta) vârfurile sale folosind culori din mulțimea astfel încât oricare două vârfuri adiacente să fie colorate diferit. Care este numărul minim de muchii ale unui graf colorabil?
Prima observație este că în colorarea grafului, trebuie ca toate culorile disponibile să fie folosite, pentru că altfel ar exista un număr mai mic de culori necesare, ceea ce încalcă definiția unui sistem. Așadar, graful trebuie să aibă noduri. În plus, trebuie să existe muchie între oricare două noduri, pentru că altfel unul dintre cele două noduri ar putea fi colorat altfel, fiind necesare mai puține culori, și iar nu s-ar respecta definiția sistemului.
Deci, răspunsul este dat de numărul de muchii ale unui graf neorientat complet cu noduri. Adică Răspunsul final este A.
Subiectul II. Problema 3.
Considerăm o matrice de dimensiune care conține numere naturale distincte două câte două. Matricea reprezintă terenul de joacă al unei broscuțe. Elementul de pe linia și coloana din matrice este înălțimea terenului la acea poziție. Broscuța vizitează o succesiune de poziții din teren în următorul fel: Broscuța se află inițial pe linia și coloana În orice poziție s-ar afla la un moment dat, broscuța efectuează un salt pe una dintre pozițiile vecine pe orizontală sau verticală.
Dintre acestea, broscuța va alege poziția care are înălțimea cea mai apropiată de înălțimea de pe poziția curentă (deci cu modulul diferenței dintre cele două înălțimi minim). În cazul în care există mai multe poziții vecine cu această proprietate, ea alege să sară pe cea cu înălțimea cea mai mică dintre acestea. Broscuța nu se oprește niciodată.
a) În exemplul de mai jos, dimensiunea terenului este Broscuța se află inițial la coordonatele unde înălțimea este Scrieți înălțimile primelor poziții vizitate de broscuță, în ordinea vizitării acestora.
Aplicând regula descrisă mai sus, primele înălțimi vizitate sunt și La primul pas, spre exemplu, se alege înălțimea corespunzătoare minimului dintre și Pentru diferența avem și Se alege minimul dintre cele două înălțimi, deci
b) Scrieți o funcție C++ care primește ca parametri matricea dimensiunile acesteia, și și numerele naturale și Funcția trebuie să returneze cea mai mică înălțime a unei poziții vizitate de broscuță de cel puțin două ori. Nu este necesară validarea parametrilor de intrare.
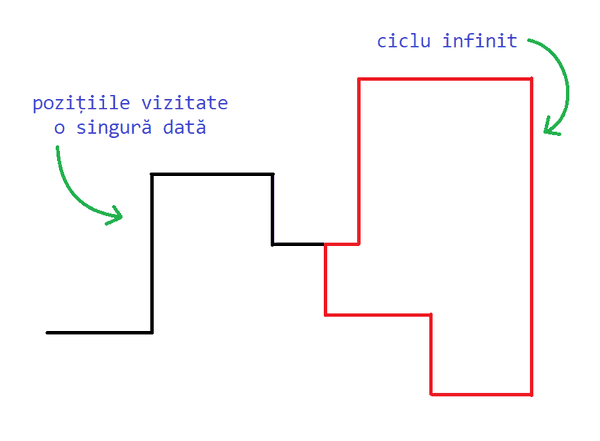
Se observă că nu toate celulele matricei vor fi neapărat vizitate. Prima dată când broscuța ajunge pentru a doua oară pe o anumită celulă, traseul ei începe să se repete, urmând să facă de o infinitate de ori aceleași mișcări făcute de la prima vizită a acelei celule până la a doua (exclusiv). Cu alte cuvinte, din clipa aceea se intră într-un ciclu infinit. Pentru calcularea minimului, ne interesează doar numerele de pe acel ciclu, pentru că doar ele sunt vizitate de cel puțin două ori.
Folosim o matrice locală aux, de tip bool, unde reținem pe fiecare poziție true dacă și numai dacă am vizitat-o. Începem să parcurgem pozițiile matricei cum este descris în enunț. Când ajungem pe una vizitată deja, îi reținem valoarea în variabila val, pentru că de acolo începe ciclul. Reținem valorile pozițiilor vizitate până atunci în vectorul v, iar la final parcurgem ciclul folosind acest vector.
// (NMAX - 1) = valoarea maximă pe care o poate lua n// (MMAX - 1) = valoarea maximă pe care o poate lua m
int findMin(int A[NMAX][MMAX], int n, int m, int L, int C) { int val; // valoarea de la care începe ciclul infinit bool aux[NMAX][MMAX] = {}; // aux este inițializată cu false
// Vectorul valorilor parcurse până la intrarea în ciclu: int lg = 0; int v[NMAX * MMAX];
// Vectorii de deplasare: int dL[] = {-1, 0, 1, 0}; int dC[] = { 0, 1, 0, -1};
while (true) { if (aux[L][C]) { // Am trecut deja pe aici. val = A[L][C]; break; } else { aux[L][C] = true; // Marcăm poziția drept vizitată v[lg++] = A[L][C]; // și îi adăugăm valoarea în vector. }
// Inițializăm coordonatele valorii căutate: int colMin = C; int linMin = L + (L > 1 ? -1 : 1); // Ne asigurăm că este una din matrice.
int dif = A[linMin][colMin] - A[L][C]; // Calculăm diferența înălțimilor. int absMin = dif < 0 ? -dif : dif; // Inițializăm modulul minim al diferenței.
// Parcurgem vecinii poziției curente: for (int i = 0; i < 4; i++) { int lin = L + dL[i]; int col = C + dC[i];
// Dacă vecinul se află în interiorul matricei: if (1 <= lin && lin <= n && 1 <= col && col <= m) { dif = A[lin][col] - A[L][C]; // diferența curentă abs = dif < 0 ? -dif : dif; // modulul diferenței curente
// Dacă am găsit o valoare/ poziție mai bună: if (abs < absMin || abs == absMin && A[lin][col] < A[linMin][colMin]) { absMin = abs; linMin = lin; colMin = col; } } }
// Actualizăm coordonatele curente: L = linMin; C = colMin; }
// Inițializăm minimul căutat cu ultima valoare din vector: int min = v[lg - 1];
// Parcurgem vectorul în sens invers, până la începutul ciclului: for (int i = lg - 2; i >= 0; i--) { min = v[i] < min ? v[i] : min;
// Am terminat! if (v[i] == val) return min; }}Subiectul II. Problema 4.
Definim un cuvânt drept șir nevid format din cel mult caractere ale alfabetului latin:
a) Scrieți o funcție C++ cu numele care are ca argument de intrare un cuvânt și returnează un număr natural. Pentru oricare două cuvinte și funcția trebuie să satisfacă proprietatea În cazul în care argumentul primit nu este cuvânt, funcția va returna
Vom reprezenta cuvintele prin șiruri de caractere (string-uri). Trebuie să găsim o funcție injectivă pe mulțimea tuturor cuvintelor. Cea mai simplă idee, inspirată din funcțiile de hashing, este să privim un cuvânt ca pe un număr scris în baza (lungimea alfabetului $ + 1$), și să îl convertim în baza Fiecărei litere îi asociem un număr cuprins între și mai exact poziția sa din alfabet. Dacă am indexa pozițiile de la și am lucra cu baza funcția n-ar mai fi injectivă. De exemplu, atât pentru cât și pentru s-ar returna
int value(char* str) { int val = 0; for (int i = 0; str[i]; i++) val = val * 27 + str[i] - 'a' + 1; return val;}b) Justificați faptul că implementarea funcției este corectă.
Funcția primește ca parametru un șir de caractere și returnează un număr natural, așa cum se cere în problemă. Funcția este injectivă deoarece unui număr scris într-o anumită bază îi corespunde exact un număr scris în altă bază. În cazul nostru, cele două baze de numerație sunt și respectiv
Subiectul III. Problema 1.
Câte șiruri distincte formate din exact o literă două litere trei litere și patru litere există?
Asta e o simplă problemă de combinatorică. Putem pune litera pe poziții. Litera poate fi pusă pe două din restul de poziții. Litera poate fi pusă pe trei dintre celelalte poziții. Litera poate fi pusă pe patru dintre cele poziții rămase. Răspunsul corect este C, și este dat de rezultatul următoarei formule:
Subiectul III. Problema 2.
Se consideră funcția recursivă de mai jos. Ce valoare va returna apelul
Trebuie să urmărim lanțul de apeluri recursive. Apelul funcționează cam așa:
F(53) =2 * F(26) =2 * (1 + F(13)) =2 * (1 + (2 * F(6))) =2 * (1 + (2 * (1 + F(3)))) =2 * (1 + (2 * (1 + (2 * F(1))))) =2 * (1 + (2 * (1 + (2 * (2 * F(0)))))) =2 * (1 + (2 * (1 + (2 * (2 * 0))))) =2 * (1 + (2 * (1 + (2 * 0)))) =2 * (1 + (2 * (1 + 0))) =2 * (1 + (2 * 1)) =2 * (1 + 2) =2 * 3 =6Deci, răspunsul este
Subiectul III. Problema 3.
Spunem că o matrice pătratică de dimensiune având elemente numere naturale, are proprietatea dacă îndeplinește următoarele condiții:
- (i) Pentru orice numărul de elemente nenule din submatricea formată din primele linii și coloane ale lui este
- (ii) Pentru orice fie fie
- (iii) Pentru orice linie a matricei, elementele nenule au aceeași valoare.
De exemplu, matricea pătratică de mai jos, de dimensiune are proprietatea
a) Scrieți o funcție C++ care primește ca parametri un întreg și o matrice pătratică de dimensiune Funcția va returna dacă matricea satisface proprietatea în caz contrar.
Verificăm, pe rând, fiecare condiție a proprietății Imediat ce ne dăm seama că una nu este îndeplinită, returnăm false.
// (NMAX - 1) = valoarea maximă pe care o poate lua n
bool check(int n, int a[NMAX][NMAX]) { int cnt = 0; // numărul curent de elemente nenule
// Condiția (i): for (int p = 2; p <= n; p++) { for (int i = 1; i < p; i++) { if (a[p][i]) cnt++; if (a[i][p]) cnt++; }
if (a[p][p]) cnt++;
if (cnt != 2 * p - 2) return false; }
// Condiția (ii): for (int i = 1; i <= n; i++) for (int j = 1; j <= i; j++) if (!(!a[i][j] && !a[j][i] || a[i][j] == a[j][i] + 1)) return false;
// Condiția (iii): for (int i = 1; i <= n; i++) { // Căutăm primul p pentru care a[i][p] != 0: for (int p = 1; !a[i][p]; p++);
for (int j = p + 1; j <= n; j++) if (a[i][j] && a[i][j] != a[i][p]) return false; } return true;}b) Demonstrați că într-o matrice pătratică de dimensiune care satisface proprietatea există cel puțin două linii având un singur element nenul.
Având în vedere că (bool) a[i][j] == (bool) a[j][i], putem considera că matricea dată este matricea de adiacență a unui graf neorientat cu noduri. Graful acesta este conex, deoarece fiecare nod este adiacent cu unul mai mic decât el (ca indice), conform condiției (ii). În plus, numărul lui de muchii este adică Având în vedere acestea, matricea dată este de fapt matricea de adiacență a unui arbore.
Dacă arborele are minim două frunze, atunci matricea are minim două linii cu o singură valoare nenulă, pentru că frunzele sunt adiacente la un singur nod. Dacă nu, arborele este practic o listă simplu înlănțuită. În acest caz, rădăcina și frunza vor reprezenta cele două linii cu o singură valoare nenulă.
c) Scrieți o funcție C++ care primește ca argumente un întreg și o matrice pătratică de dimensiune care îndeplinește proprietatea Funcția va afișa cea mai lungă secvență de indecși care satisface relația pentru orice Nu este necesară validarea parametrilor de intrare. Justificați corectitudinea algoritmului. Pentru exemplul de mai sus, funcția va afișa Nu se acordă puncte pentru soluții ce folosesc backtracking.
În exemplul dat se observă că dacă este nenul, atunci nivelul lui este De asemenea, întotdeauna primul nod este rădăcina arborelui, conform condiției (ii). Deci, trebuie determinat un lanț de la cea mai adâncă frunză la rădăcină. Ideea pe caz general este aproape la fel, doar că nu scrie nicăieri că nivelurile se indexează de la Așadar, trebuie să avem grijă să ne oprim după ce am afișat nodul și nu nodul de pe nivelul
// (NMAX - 1) = valoarea maximă pe care o poate lua n
void maxPath(int n, int a[NMAX][NMAX]) { int levels[NMAX]; // nivelurile nodurilor int leaf = 1; // Inițializăm frunza cu rădăcina. for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) if (a[i][j]) { levels[i] = a[i][j]; // Actualizăm nivelul, if (levels[i] > levels[leaf]) // și dacă e cazul, leaf = i; // frunza. break; }
// Afișăm lanțul de la frunză la rădăcină: cout << '('; while (true) { cout << leaf << ", "; for (int j = 1; j <= n; j++) if (a[j][leaf] && levels[j] == levels[leaf] - 1) { leaf = j; // leaf devine nodul curent break; }
// Dacă am ajuns la rădăcină: if (leaf == 1) { cout << "1)\n"; break; } }}Voi ce părere aveți despre subiectele date la admiterea la Facultatea de Informatică din Iași, 2018? Mie mi se par ceva mai grele decât cele de anul trecut, dar în continuare suficient de accesibile. Dacă aveți vreo întrebare despre problemele rezolvate în acest articol, nu ezitați să o lăsați mai jos pentru a vă putea răspunde
PS: Wow, 2595 de cuvinte! Cred că merită un share articolul